Министерство образования и науки Самарской области

Государственное автономное учреждение дополнительного профессионального образования Самарской области

ИНСТИТУТ РАЗВИТИЯ ОБРАЗОВАНИЯ

Итоговая работа

на тему: «Проектирование учебного занятия по математике на основании примерной рабочей программы основного общего образования «Математика» в соответствии с требованиями ФГОС ООО».

на курсах повышения квалификации:

«Обновление содержания и методик преподавания в соответствии

с требованиями ФГОС (ООО, математика)»

(по государственному заданию МОиН СО)

Выполнил(а): Антонова А. А

Место работы: МБУ «Гимназия 48»

Руководитель:

Бобрович Елена Михайловна, преподаватель кафедры

математического и естественнонаучного образования

ГАУ ДПО СО ИРО bobrovitchelena@yandex.ru

20.03 -24.03.2023 г.

Самара 2023 г.

ID программы:2327; ID группы: 15042

«Проектирование учебного занятия по математике на основании примерной рабочей программы основного общего образования «Математика» в соответствии с требованиями ФГОС ООО».

УМК «Алгебра» 8 класс Мордкович А.Г.

Тема: Функция y=k/x, ее свойства и график.

Целии задачи: ввести понятие функции обратная пропорциональность, изучить её свойства, формировать умение строить график функции.

Тип урока: урок открытия новых знаний.

Планируемые результаты:

Предметные:

Овладение понятием обратно пропорциональной зависимости, умение строить графики функций, описывать их свойства, использовать функционально-графические представления для описания и анализа реальных зависимостей.

Метапредметные:

Определить и сформулировать цель с помощью учителя, спланировать свои действия в соответствии с поставленной задачей, развивать навыки самостоятельности в работе, самоанализа и самоконтроля при оценке результата и процесса своей деятельности. Учиться оформлять свои мысли в устной и письменной форме, учиться слушать и понимать речь других.

Личностные: Проанализироватьполученные знания (ответить на вопросы, используя свой жизненный опыт и информацию, полученную на уроке).

---

Используемое оборудование: компьютер, мультимедийный проектор, презентация

Содержательная часть

Этап урока	Деятельность учителя. Задания для учащихся.	Деятельность учащихся.	Планируемые результаты предметные УУД
1. Организационный 2 мин.	Приветствие, проверка готовности к уроку	Готовят своё рабочее место. Включаются в деловой ритм урока. Получают листы самооценки.	Регулятивные: организуют своё рабочее место.
2. Мотивация	Напоминает о том, что ранее рассматривали функциональные зависимости или функции. Какие вы можете вспомнить?	Вспоминают ранее изученный материал, приводят примеры.	Предметные: уметь ориентироваться в своей системе знаний.
3 Актуализация	Вспомните основные понятия, связанные с функциями. Даёт задание разгадать кроссворд на основные понятия, связанные с функциями (работа в группах).	Разгадывают кроссворд.	Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.
4 Повторение ранее полученных знаний.	Показывает ответы на кроссворд.	Проверяют ответы.	Личностные: самостоятельное определение качества ранее полученных знаний. Регулятивные: оценка, выделение и осознание того, что усвоено ранее.
5 Реализация цели.	Предлагает продолжить фразу - с уменьшением скорости на данном отрезке пути время движения… -с увеличением производительности труда при выполнении данного объёма работы время работы … Это примеры каких зависимостей? В явлениях природы, в человеческой деятельности часто встречаются обратно пропорциональные зависимости.	Отвечают на вопросы	Регулятивные: соотнесение того, что уже известно и того, что ещё не известно.
4 Постановка цели урока	Ребята. С чем сегодня будет связана тема урока.	Формулируют цель . Записывают тему урока.	Личностные: самостоятельное выделение и формулирование познавательной цели. Регулятивные: оценка, выделение и осознание того, что уже усвоено и что нужно усвоить
5.Реализация цели	Рассмотрим один из примеров обратной пропорциональности. (Демонстрирует прямоугольник, у которого изменяется одна из сторон, площадь при этом остаётся той же. Задаёт вопросы). Пусть площадь прямоугольника равна 8, тогда можно написать формулу ху=8 . Посмотрим, что будет происходить со стороной у, если будем изменять сторону прямоугольника x. (при этом площадь не меняется) Если х уменьшается в 2 раза, то у увеличивается в 2 раза; если х увеличить в 2, 5 раза, то у уменьшится в 2, 5 раза. И наоборот при увеличении у в несколько раз, х уменьшится во столько же раз, при уменьшении у в несколько раз х увеличится во столько же раз. Какую зависимость между величинами х и у мы наблюдаем? Запишем формулой зависимость у от х. Запись на доске y= 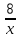Мы имеем записанную формулой функцию, которая называется обратной пропорциональностью. В нашем примере со сторонами прямоугольника, значения х,у были положительными по условию. В функции значения х,у могут быть как положительными , так и отрицательными , кроме числа…(о), почему? В общем виде функция записывается y= , где k- число, k≠0, х- независимая переменная. В нашем примере чему равно k? Ребята. Заполним таблицу 1 значений. Заполните таблицу значений. (работа в парах) Организует проверку таблицы Задаёт вопросы, связанные с построением графика функции. По данным значениям (x;y), указанным в таблицах, построить на координатной плоскости точки. Соотнесите размер тетрадного листа с числами в таблице. Что примем за единичный отрезок? ( одну клетку тетради, оси координат на всю страницу) Проверяется построение точек в координатной плоскости.(на доске) Как же получить графики функций y= 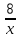? (соединить плавной линией точки, построенные на координатной плоскости). В каких четвертях расположены точки? Одних точек недостаточно для построения графика функции, поэтому выясним особенности графика и тогда уже его построим. Назовите область определения функции (х ≠0) (это означает, что нет точек с абсциссой 0, значит график функции не пересекает ось OY). Может ли у принимать значение 0? (нет, это означает, что график функции не пересекает ось OX). Для точек, расположенных в первой четверти, положительным значениям x соответствуют положительные значения у. По значениям в таблице мы понимаем- чем больше значение х, тем меньше значение у, тем ближе точка к оси абсцисс. Чем ближе положительная абсцисса к 0, тем больше ордината точки. Соедините точки плавной линией и продолжите её. Получили одну ветвь графика, расположенную в первой четверти. Вторая ветвь графика будет ей симметрична относительно начала координат и расположена в 4 четверти. (демонстрирует на доске) Построен график график функции y=	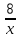Обсуждают и отвечают на вопросы. Делают запись в тетради. Заполняют таблицу Обсуждают результаты. Заканчивают предложение, отвечают на вопросы. Соотносят размер тетрадного листа с числами в таблице. Отмечают точки в координатной плоскости Проверяют построенные точки. Отвечают на вопросы, строят график функции.	Познавательные: умение логически мыслить, устанавливать причинно-следственные связи. Коммуникативные: умение слушать и понимать речь учителя, участвовать в коллективном обсуждении проблем, сотрудничество со сверстниками
Физкультминутка	Организует выполнение упражнений	Выполняют упражнения.
6.Работа в группе.	Пишет формулу, задающую функцию и даёт задание заполнить выданную таблицу 2 значений ( проверяются значения) . Постройте график функции y= – 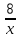, используя свойства этой функции (работа в парах). (проверяется вид графика с помощью демонстрации на экране)	Заполняют таблицу. Обсуждают результаты строят график функции.	Личностные: умение работать в команде Предметные: умение применять новые знания.
7. Соотнесение полученных результатов.	По результатам проведённой работы задаёт вопросы о влиянии знака коэффициента на вид графика функции. Чему равно значение k в каждой из рассмотренных функций ? Как расположены графики в зависимости от k? График функции y= состоит из двух ветвей симметричных относительно начала координат и называется гиперболой.	Отвечают на вопросы, соотносят полученные результаты. Записывают в тетрадь значения k .	Познавательные: умение ориентироваться в своей системе знаний, поиск и выделение необходимой информации
8. Самостоятельная работа с последующей проверкой.	Построить график функции y= . Сначала составим таблицу значений (на доске), возьмём по 4 значения отрицательных и положительных. а) найдите по графику значение y при x=3; -5 б) найдите по графику значение аргумента, при котором значение функции равно -4; 6 значения, найденные по графику будут… Ответ оформите в виде таблицы. В процессе работы задаёт наводящие вопросы.	Обсуждают в группе таблицу, заполняют таблицу значений и стоят график, отвечают на вопросы по графику, обсуждают ответы. Заканчивают предложение.	Регулятивные: оценка, выделение и осознание того, что усвоено. Личностные: умение работать в команде.
9. Закрепление полученных знаний.	Проверяет построенный график. Задаёт вопросы на распознавание функции обратная пропорциональность по формуле, определить принадлежит ли точка с данными координатами графику данной функции..	Показывают построенный график, отвечают на вопросы.	Регулятивные: оценка, выделение и осознание того, что усвоено.
10. Подведение итогов урока.	Задаёт вопросы. Что узнали нового на уроке? Что понравилось делать?	Обобщают изученное на уроке.
11. Рефлексия.	Организовать оценивание собственной деятельности на уроке.	Работают с оценочными листами.	Личностные: готовность оценивать свой учебный труд, проведение самооценки работы на уроке на основе критерия успешности учебной деятельности, оценка процесса и результата деятельности.

---

Раздаточный материал к уроку

Лист 1

											12
									2
							1
3					9
									5
	10
8			6								4
								11 7

---

По горизонтали

3. Множество точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – значениями функции

5. Как называется число k в формуле y=kx+b? (… коэффициент)

8. Слово в названии функции y=kx

11. Буква латинского алфавита, которой часто обозначают функцию

По вертикали

1. Зависимость между переменными, при которой каждому значению независимой переменной соответствует значение зависимой переменной

2. Независимая переменная или …

4. Функция, заданная формулой y=kx+b

6. Что является графиком линейной функции?

7. Если k≠0, то график функции y=kx+b пересекает эту ось, а если k=0, то параллелен ей. Какой буквой обозначается эта ось?

9. Функция y=x²

10. Название графика квадратичной функции

12. Один из способов задания функции

Лист 2

у =

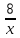
Таблица 1

х	-8	-5	-4	-2	-1	-		1	2	4	5	8
у

у= -

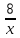
Таблица 2

х	-8	-5	-4	-2	-1	-		1	2	4	5	8
у

---

Карточка самооценивания

Ф. И._________________________

«+» - справились с заданием

«±» - справились, но возникли сложности

«-» - не справились

№	Задание	Оценка
1	Кроссворд
2	Таблица 1
3	Таблица 2
4	Построение графиков
5	Активность на уроке

4,5 – 5 «+» - оценка «5»

3,5 – 4 «+» - оценка «4»

2,5 – 3 «+» - 0ценка «3»

Оценка

---

Смотрите также файлы

• Что такое синонимы.docx

• Гостиничные цепи.docx

• Для какого вида деятельности не требуется получения лицензии.docx

• Реферат по дисциплине Основы противодействия коррупции.docx

• Отчет по проделанной работе в соответствии с требованием ескд. Отчеты по всем работам помещаются в отдельной тетради или папке, которая после окончания цикла работ сдается на кафедру.doc