Файл: Анализ данных и моделирование транспортных процессов.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 26.10.2023

Просмотров: 55

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


Федеральное агентство железнодорожного транспорта
Сибирский государственный университет путей сообщения
Кафедра «Железнодорожные станции и узлы»

(название кафедры)

АНАЛИЗ ДАННЫХ И МОДЕЛИРОВАНИЕ ТРАНСПОРТНЫХ ПРОЦЕССОВ
Расчётно-графическая работа

(вид работы)

по дисциплине «Математическое моделирование систем и процессов»

(название дисциплины)
Пояснительная записка

(вид документа)

ЖДСУ.Д313.00.00.00.00 ПЗ

(обозначение документа)
Руководитель Разработала

доцент студент гр. Д-313

_________________/ Карасёва А.А. ________________/Валов А.К.

(подпись) (подпись)

_________________ _________________

(дата) (дата)
Краткая рецензия:

__________________________________________________________________

__________________________________________________________________

__________________________________________________________________

__________________________________________________________________

__________________________________________________________________

______________________________

(запись о допуске к защите)

______________________________ _____________________________

(оценка по результатам защиты) (подпись руководителя)

2023 г.


СОДЕРЖАНИЕ




ВВЕДЕНИЕ 5

1ПОСТРОЕНИЕ РЕГРЕССИОННОЙ МОДЕЛИ ВРЕМЕНИ ВЫПОЛНЕНИЯ ОПЕРАЦИЙ 6

2АНАЛИЗ ВЫБОРОЧНЫХ ДАННЫХ О РАБОТЕ ТРАНСПОРТНОГО ОБЪЕКТА 9

3РАСЧЕТ ПОКАЗАТЕЛЕЙ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ (СМО) 14

4ЗАДАЧА РАЦИОНАЛЬНОГО РАСПРЕДЕЛЕНИЯ ОБОРУДОВАНИЯ 17

ЗАКЛЮЧЕНИЕ 19


ВВЕДЕНИЕ




Целью выполнения расчетно-графической работы является закрепление навыков использования методов математического моделирования при решении задач исследования и развития транспортных систем и процессов.

В процессе работы необходимо решить следующие задачи:

1. Построить регрессионную модель времени выполнения операций на контейнерном терминале.

2. Выполнить анализ случайных данных о работе контейнерного терминала с использованием методов математической статистики.

3. Произвести расчет показателей контейнерного терминала, рассматривая его в виде модели системы массового обслуживания. Решить задачу совершенствования путевого развития и технического оснащения контейнерного терминала.

4. Решить задачу рационального распределения оборудования (погрузчиков) между несколькими контейнерными терминалами для получения максимального эффекта от его использования.

Результатами решения поставленных задач должны стать обоснованные предложения по повышению эффективности транспортных систем и процессов.

  1. ПОСТРОЕНИЕ РЕГРЕССИОННОЙ МОДЕЛИ ВРЕМЕНИ ВЫПОЛНЕНИЯ ОПЕРАЦИЙ




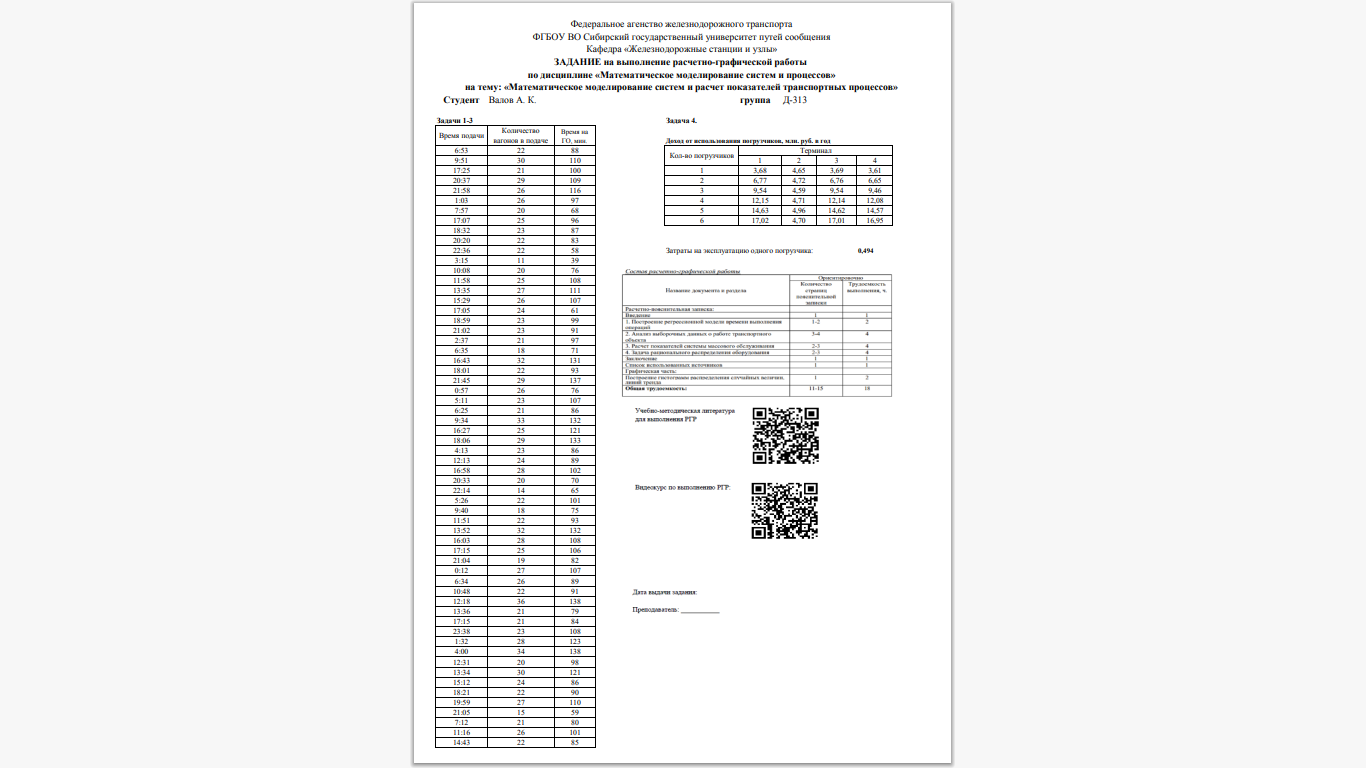
В качестве рассматриваемого объекта принимается терминал Е. Схема терминала приведена на рисунке 1.1.



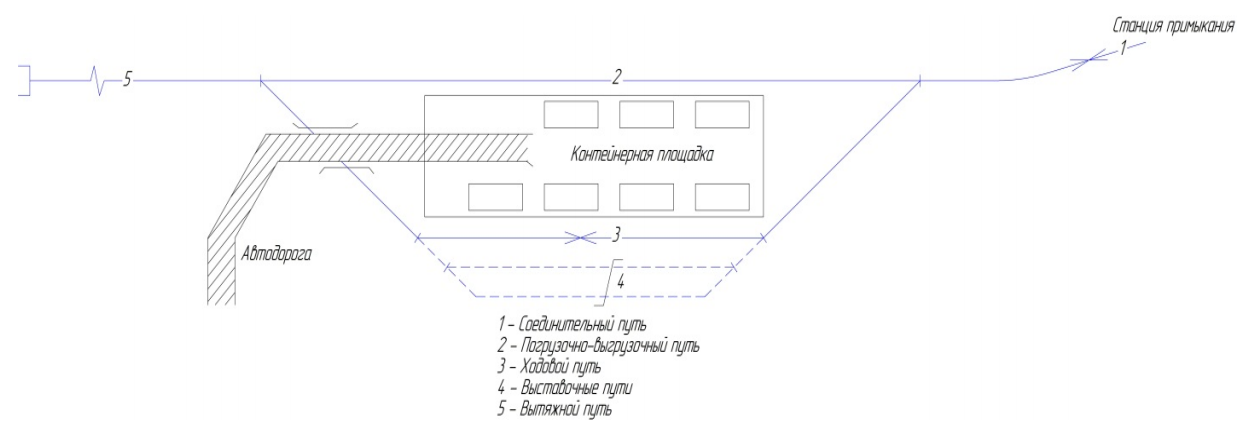
Рисунок 1.1 – Схема терминала Е

Технология работы терминала со станции примыкания по соединительному пути на терминал поступают подачи вагонов с контейнерами. Вагоны попадают на вытяжной путь, на котором составы расформировывают, а затем вагоны с контейнерами попадают на погрузочно-разгрузочные пути, где производится погрузка и выгрузка контейнеров. Их обслуживают на контейнерной площадке с помощью ричстакеров. На выставочных путях отстаивают вагоны, ожидающие отправки. После выгрузки контейнеров их грузят на автотранспорт, который подъезжает к контейнерной площадке по автодороге.

Исходные данные о работе терминала приведены в пункте 1 задания.

Сначала выполняется корреляционный анализ данных с целью выявления зависимости между числом вагонов в подаче и временем выполнения грузовых операций. Коэффициент корреляции определяется с помощью функции «Анализ данных. Корреляция» Microsoft Exсel и составляет r=0,8593, что свидетельствует о сильной зависимости наборов данных.

Далее строится диаграмма рассеивания, представленная на рисунке 1.2, ее вид подтверждает наличие линейной зависимости данных. Регрессионная модель подбирается с помощью линии тренда на диаграмме рассеивания, используются степенная функции.



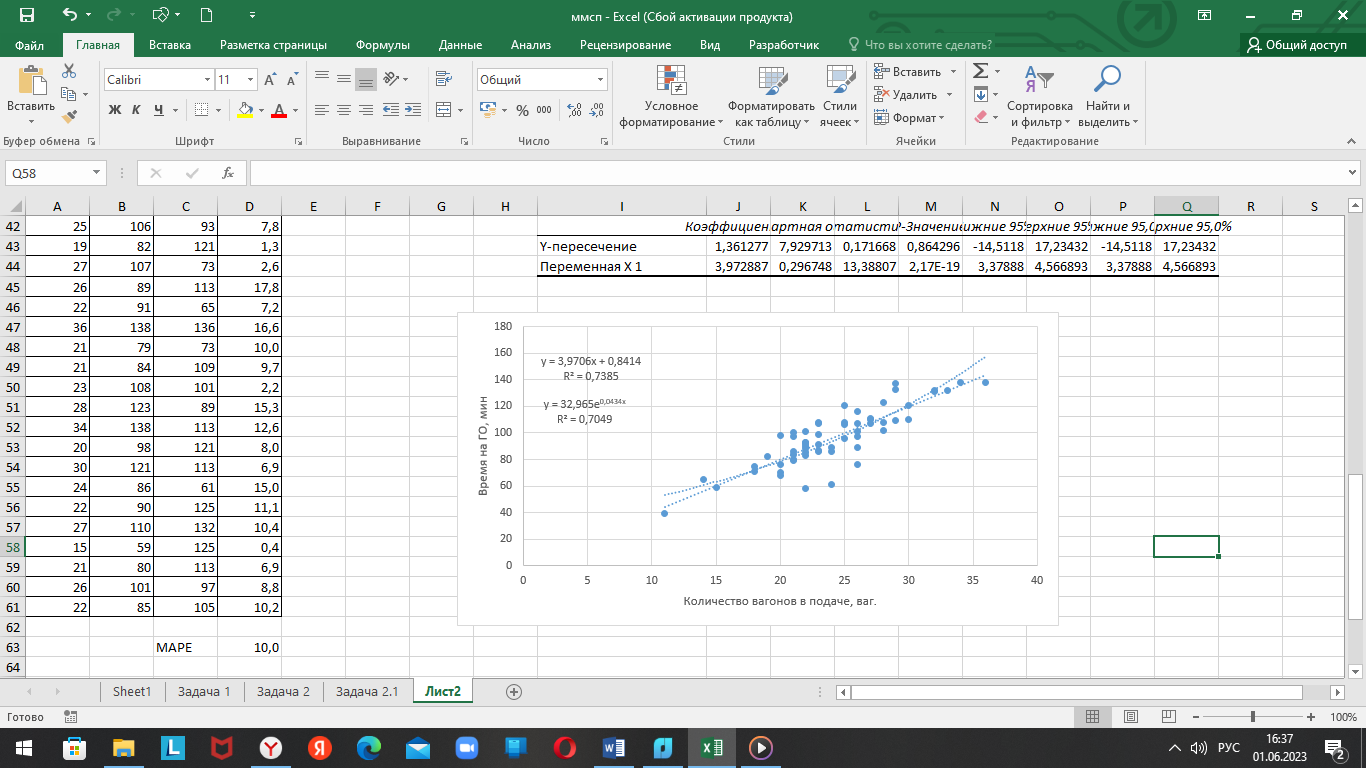
Рисунок 1.2 – Диаграмма рассеивания и подбор линии тренда

Коэффициенты аппроксимации для линейной и экспоненциальной функций практически одинаковы ????2 = 0,7385 и близки к 1, что говорит о достаточно высокой точности регрессионных моделей.

Уравнение регрессионной модели линейного типа имеет вид:


го
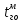 = 0,8414+3,9706m, (1.1)


го
где 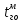– время выполнения грузовых операций, полученное с помощью модели, мин; ???? – количество вагонов в подаче.

Для линейной зависимости определяется значение средней абсолютной ошибки MAPE, %, в формате таблицы 1.2 по формуле:



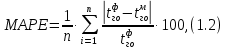
где 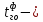фактическое время выполнения грузовых операций, мин; 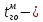время выполнения грузовых операций, полученное с помощью модели, мин.

Таблица 1.2 – Расчет средней абсолютной ошибки MAPE


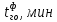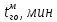Отклонение, %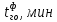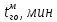




Отклонение, %

88
88
0,2
86
92
7,2

110
120
9,1
89
96
8,0

100
84
15,8
102
112
9,8

109
116
6,4
70
80
14,6

116
104
10,3
65
56
13,2

97
104
7,3
101
88
12,7

68
80
18,0
75
72
3,6

96
100
4,3
93
88
5,2

87
92
5,9
132
128
3,1

83
88
6,3
108
112
3,7

58
88
52,1
106
100
5,6

39
45
14,1
82
76
7,0

76
80
5,6
107
108
1,0

108
100
7,3
89
104
16,9

111
108
2,7
91
88
3,1

107
104
2,7
138
144
4,2

61
96
57,6
79
84
6,6

99
92
6,9
84
84
0,3

91
92
1,3
108
92
14,7

97
84
13,2
123
112
8,9

71
72
1,8
138
136
1,6

131
128
2,4
98
80
18,1

93
88
5,2
121
120
0,9

137
116
15,3
86
96
11,8

76
104
36,9
90
88
2,0

107
92
13,9
110
108
1,8

86
84
2,1
59
60
2,4

132
132
0,1
80
84
5,3

121
100
17,3
101
104
3,0

133
116
12,8
85
88
3,8

МАРЕ
9,2

Значение средней абсолютной ошибки MAPE=9,2% (10,0<20), что свидетельствует о высокой точности подобранной регрессионной модели.

  1. АНАЛИЗ ВЫБОРОЧНЫХ ДАННЫХ О РАБОТЕ ТРАНСПОРТНОГО ОБЪЕКТА



Для удобства обработки данные о времени подачи вагонов на контейнерный терминал преобразуются в интервалы между подачами и сводятся в таблицу 2.1.

Таблица 2.1 – Преобразованные данные о работе контейнерного терминала



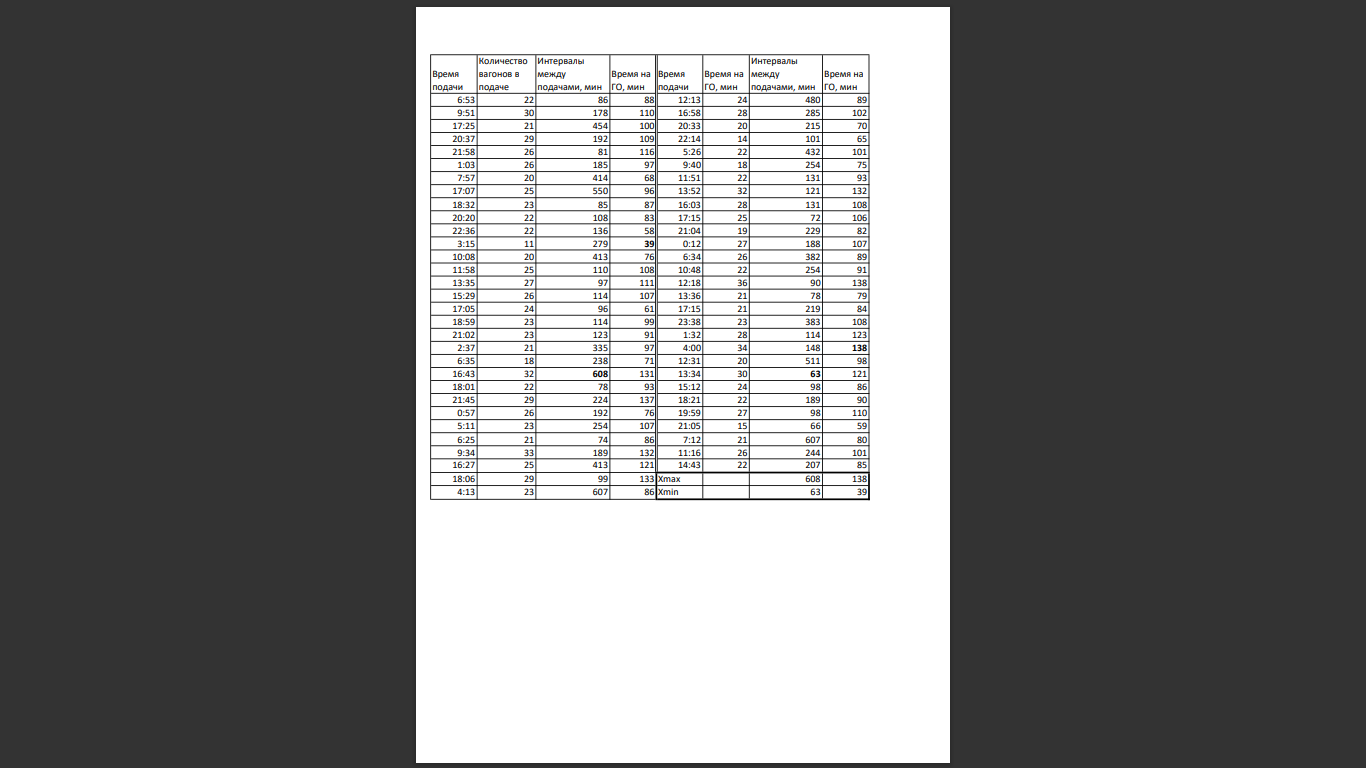
Для двух случайных величин – интервалы между подачами 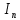и времени выполнения грузовых операций 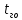– определяются следующие числовые характеристики:

1) Математическое ожидание случайной величины (измеряется в том же единице измерения, что и сама случайная величина):



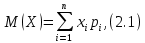
где 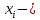i-е значение случайной величины, 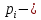вероятность появления i-ой случайной величины, 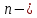количество возможных значений, которые может принимать случайная величина.

2) Дисперсия:



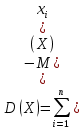
3) Среднее квадратическое отклонение случайной величины:



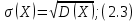
4) Коэффициент вариации – характеристика, отражающая степень отклонения значений случайной величины от ее среднего в относительном виде:



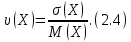
Для удобства обработки данных время подачи вагонов представляется в формате интервалов между подачами. При большом количестве значений случайной величины рассматривают разряды, являющиеся числовыми интервалами, в которые попадает то или иное количество ее значений. Количество разрядов случайной величины определяется следующим образом:



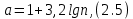
где 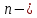количество измерений в выборке, равное 60. .

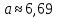Длина разряда:



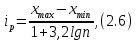
Длина разряда 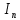: 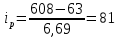; длина разряда 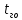: 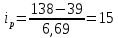. Расчет числовых характеристик случайных величин сведен в таблицы 2.1, 2.2.

Таблица 2.1 – Расчет числовых характеристик случайной величины

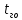
Разряды случайной величины
Среднее значение величины в разряде
Количество попаданий случайной величины в разряд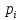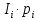


, мин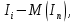


мин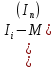


мин2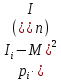
,

мин2

39-54
46,5
1
0,02
0,78
-49,9
2490
41,5

54-69
61,5
5
0,08
5,13
-34,9
1218
101,5

69-84
76,5
10
0,17
12,75
-19,9
396
66

84-99
91,5
18
0,3
27,45
-4,9
24
7,2

99-114
106,5
15
0,25
26,63
10,1
102
25,5

114-129
121,5
4
0,07
8,1
25,1
360
42

129-138
133,5
7
0,12
15,58
37,1
1376,4
160,6

Итого
60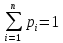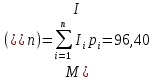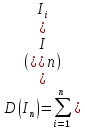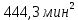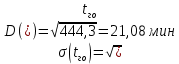












Таблица 2.2 – Расчет числовых характеристик случайной величины

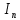
Разряды случайной величины
Среднее значение величины в разряде
Количество попаданий случайной величины в разряд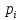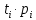


, мин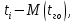


мин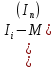


мин2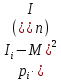
,

мин2

63-144
103,5
26
0,43
44,8
-122,1
14912,5
6462,1

144-225
184,5
12
0,2
36,9
-41,1
1690,6
338,1

225-306
265,5
8
0,13
35,4
39,8
1590,7
212,1

306-387
346,5
3
0,05
17,3
120,8
14612,8
730,6

387-468
427,5
5
0,08
35,6
201,8
40756,9
3396,4

468-549
508,5
2
0,03
16,9
282,8
80023
2667,4

549-608
578,5
4
0,07
38,5
352,8
124526,6
8301,8

Итого
60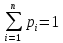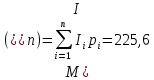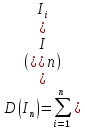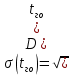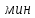










Расчет числовых характеристик интервалов времени между подачами и времени выполнения грузовых операций в Excel представлен в таблице 2.3.

Таблица 2.3 – Расчет числовых характеристик интервалов времени между подачами и времени на грузовые операции в Excel

Характеристика случайной величины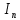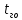




Среднее
225,26
96,4

Стандартная ошибка
19,93
2,81

Медиана
188,5
96,5

Мода
413
108

Стандартное отклонение
154,39
21,76

Дисперсия выборки
23836,84
473,87

Эксцесс
0,25
-0,08

Асимметричность
1,11
-0,02

Интервал
545
99

Минимум
63
39

Максимум
608
138

Сумма
13516
5784

Счет
60
60


Гистограммы, по которым определяются законы распределения случайных величин 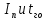представлены на рисунках 2.1 и 2.2.


103 184 265 346 427 508 578


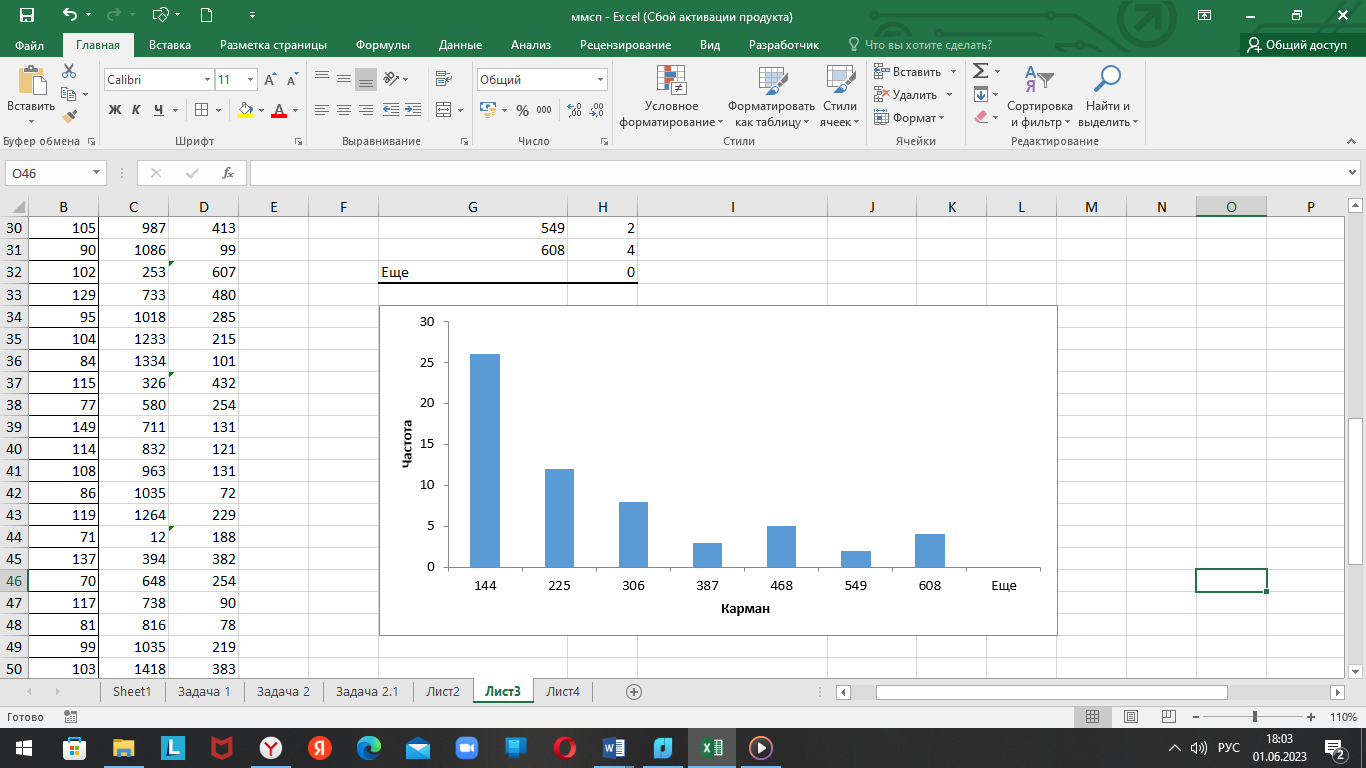
Рисунок 2.1 – Гистограмма распределения случайной величины

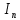
По внешнему виду гистограммы можно сделать вывод, что случайная величина 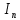– эрланговское распределение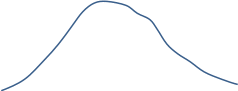


46 61 76 91 106 121 133


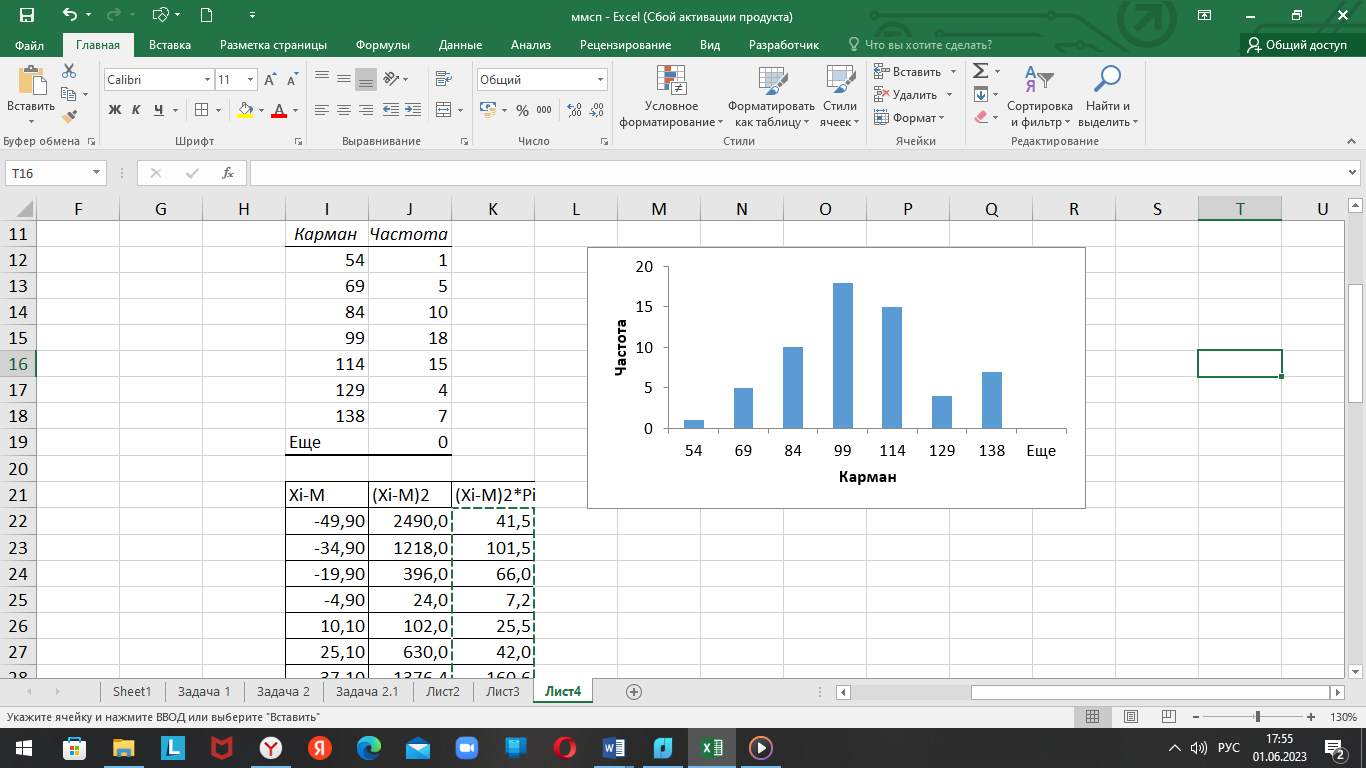
Рисунок 2.2 – Гистограмма распределения случайной величины

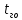
По внешнему виду гистограммы можно предположить, что это нормальное распределение.

  1. РАСЧЕТ ПОКАЗАТЕЛЕЙ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ (СМО)




С целью определения рационального оснащения терминала Е необходимо рассчитать показатели эффективности работы СМО для различных вариантов технического обслуживания: длину очереди ( 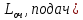и среднее время нахождения в очереди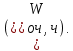

Во второй задаче в ходе анализа данных о работе терминала были определены законы распределения: входящего потока – эрланговский, и времени обслуживания – нормальный.

Интенсивность поступления требований и их обслуживание, подач/час:



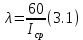
где 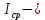интервал времени между подачами, мин;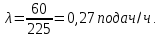



Интенсивность обслуживания поступающих требований, подач/ч:



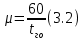
где 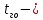время на погрузку-выгрузку одной подачи, мин;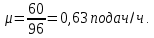



Приведенная интенсивность:





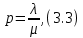
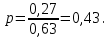
Коэффициенты неравномерности для эрланговского входящего потока и произвольного распределения времени обслуживания:





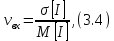
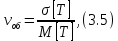
где 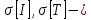среднеквадратические отклонения случайных величин , мин; 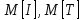– математические ожидания величин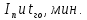





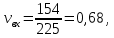
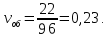
Время нахождения в очереди:





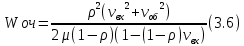
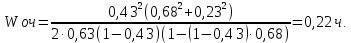
Длина очереди:






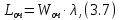
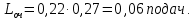
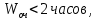значит, дополнительное техническое оснащение не требуется.

Рассматриваются возможные варианты увеличения перерабатывающей способности контейнерного терминала:

1) Обслуживание производится одним ричстакером на одном погрузочно- выгрузочном пути – одноканальная система массового обслуживания (СМО).

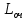= 0,06 ≈ 1 дополнительный выставочный путь. Стоимость укладки одного пути Сп = 2,5 у. е.

2) Два ричстакера объединены в один канал обслуживания – одноканальная СМО.

????2 = 2???? = 2 0,63 = 1,26 подач/час;

???? = = ;



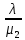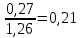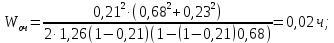
Стоимость одного ричстакера ср = 10 у. е.

3) Ричстакеры работают как два отдельных канала обслуживания (на двух путях) с интенсивностью μ, т.е. число каналов обслуживания ???? = 2 – многоканальная СМО.

Загрузка системы:





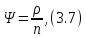
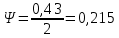
Время нахождения в очереди:









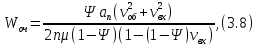
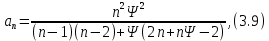
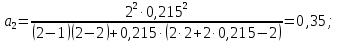
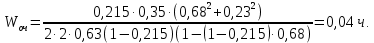
Стоимость данной системы включает укладку дополнительного погрузочно-выгрузочного пути и покупку ричстакера спр = 2,5 + 10 = 12,5 у.е.

Наиболее целесообразной будет реализация первого варианта – использование одноканальной системы массового обслуживания с одним ричстакером на одном погрузочно- выгрузочном пути.

  1. ЗАДАЧА РАЦИОНАЛЬНОГО РАСПРЕДЕЛЕНИЯ ОБОРУДОВАНИЯ


Исходные данные представлены в таблице 4.1.

Таблица 4.1 – Доход от использования погрузчиков, млн. рублей в год

Кол-во погрузчиков
Терминал

1
2
3
4

1
3,68
4,65
3,69
3,61

2
6,77
4,72
6,76
6,65

3
9,54
4,59
9,54
9,46

4
12,15
4,71
12,14
12,08

5
14,63
4,96
14,62
14,57

6
17,02
4,7
17,01
16,95

Расходы на эксплуатацию одного погрузчика – 0,494 млн. руб. в год


Основное рекуррентное уравнение динамического программирования в общем виде:



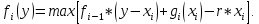
Частичный расчёт значений функции



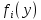
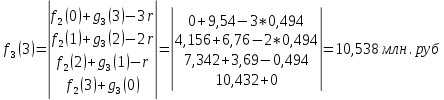
Итоговая таблица с рассчитанными значениями функции полученного эффекта 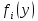представлена в таблице 4.2.

Таблица 4.2 – Итоговая таблица с рассчитанными значениями функции полученного эффекта

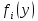
Y
Терминал 1
Терминал 2
Терминал 3
Терминал 4

















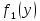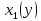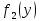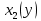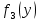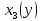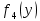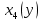1
3,186
1
4,156
1
4,156
0
4,156
0

2
6,276
2
7,342
1
7,352
1
7,352
0

3
9,046
3
10,432
1
10,538
1
10,538
0

4
11,656
4
13,202
1
13,628
1
13,654
1

5
14,136
5
15,812
1
16,398
1
16,744
1

6
16,526
6
18,292
1
19,008
1
19,514
1

Таким образом, можно сделать вывод, что наиболее рациональным вариантом распределения погрузчиков между всеми четырьмя терминалами, является отправка 1 погрузчика на 4 терминал, 1 – на 3 терминал, 1 – на 2 терминал и 3 – на 1 терминал соответственно. 19,514 млн.руб/год – прибыль от рационального распределения оборудования на терминале.

ЗАКЛЮЧЕНИЕ



Корреляционный анализ выявил сильную зависимость между числом вагонов в подаче ???? и временем выполнения грузовых операций ????го. Коэффициент корреляции составляет r=0,8593. Построена диаграмма рассеивания случайной величины ????го и подобрано уравнение регрессионной модели степенного типа = 0,8414+3,9706m. Значение средней абсолютной ошибки MAPE=9,2 % свидетельствует о высокой точности модели.

При выполнении задания по анализу выборочных данных о работе транспортного объекта были рассчитаны основные числовые характеристики двух случайных величин: интервалов между подачами ????п и времени выполнения грузовых операций ????го. Характеристики интервалов между подачами: математическое ожидание 225,26 мин; дисперсия 23836,84 мин2; среднее квадратическое отклонение 154,39 мин. Характеристики времени выполнения грузовых операций: математическое ожидание 96,4 мин; дисперсия 473,87 мин2; среднее квадратическое отклонение 21,76 мин. Построены гистограммы ряда распределения и функции распределения случайных величин. Законы распределения ????п – эрланговское, ????го – нормальное.

При расчете показателей работы СМО (контейнерного терминала) определены длина очереди ????оч = 0,06 подач, время ожидания в очереди ????оч = 0,22 ч. Определены возможные варианты увеличения перерабатывающей способности контейнерного терминала.

С использованием основного рекуррентного уравнения динамического программирования были рассчитаны значения функции рационального распределения погрузчиков между терминалами ????????(????). Наиболее рациональным вариантом распределения погрузчиков является отправка 1 погрузчика на 4 терминал, 1 – на 3 терминал, 1 – на 2 терминал и 3 – на 1 терминал соответственно. 19,514 млн.руб/год – прибыль от рационального распределения оборудования на терминале.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

  1. Акулиничев, В. М. Математические методы в эксплуатации железных дорог: учеб. пособие для вузов ж. -д. трансп. / В. М. Акулиничев, В.А. Кудрявцев, А. Н. Корешков. – М.: Транспорт, 1981. – 223 с.

  2. Гладких, Б. А. Методы оптимизации и исследование операций для бакалавров информатики: учебное пособие / Б. А. Гладких. – Томск: Издательство «НТЛ», 2011. – Ч. 2. Нелинейное и динамическое программирование. – 264 с. – ISBN 978-5-89503-483-5; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=200917.

  3. Никифорова, Н. Г. Статистика: теория и практика в Excel: учебное пособие. Н. Г. Никифорова, В. С. Лялин, И. Г. Зверева. – М.: Финансы и статистика, 2010. – 448 с. – ISBN 978-5-279-03381-2; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=78916.

Смотрите также файлы