Файл: Практическая работа по дисциплине Программные статистические комплексы По теме Контрольные карты Шухарта в Statistics Tollbox matlab.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 133
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской ФедерацииФедеральное государственное бюджетное образовательное учреждение высшего образования«Владимирский государственный университетимени Александра Григорьевича и Николая Григорьевича Столетовых»(ВлГУ)Кафедра «Управление качеством»Практическая работа по дисциплине «Программные статистические комплексы»
Такими характеристиками являются выборочное среднее и медиана (характеристики положения), а также размах и выборочное среднее квадратическое отклонение (характеристики рассеяния случайной величины Х).На контрольную карту наносят значения некоторой статистической характеристики (точки), которые рассчитываются по данным выборок в порядке их получения, верхнюю и нижнюю контрольные границы Кв (или UCL) и Кн (или LCL), верхнюю и нижнюю границы технических допусков Тв и Тн (при их наличии), а также среднюю линию (CL). Иногда используют также предупредительные границы Кп.По количественным признакам используют в основном следующие контрольные карты:- карта средних арифметических значений ( — карта);- карта медиан ( — карта);- карта средних квадратичных отклонений (s -карта);- карта размахов (R -карта).Для – карты и - карты – рассчитывают две границы регулирования или контроля: верхнюю и нижнюю.Для s – карты и R - карты – достаточно рассчитать по одной границе контроля - верхней, так как можно следить лишь за увеличением рассеивания.Карта средних арифметических значений ( —карта) используется для контроля отклонения параметра от нормы и настройки в норму. Точки на контрольной карте — это средние значения небольших выборок, обычно одинакового объема, с 3 до 10 элементов: ,где n — объем выборки (подгруппы).Для получения выборок можно использовать результаты измерений, проводившихся через равные промежутки времени, путем разбиения их на группы.Среднюю линию рассчитывают как среднее из средних значений выборок:
s - карте используют только верхнюю границу.Карта размахов (R-карта) используется вместо карты средних квадратических отклонений, когда хотят упростить расчеты. При этом карта размахов менее точна.При построении R-карты берут 20…30 выборок одинакового объема от 2 до 10 элементов. Точки на карте - размахи выборок.Размах выборки R — это разность между максимальным xmax и минимальным xmin значениями выборки. Средняя линия - это среднее размахов выборок. Контрольные границы рассчитывают по формулам: , При уровне значимости 0,0027 коэффициенты D3 и D4 можно найти из табл. 4.2. При n <7 нижняя контрольная граница не используется. Таблица 4.2. Значение коэффициентов для R-карты
Часто при статистическом регулировании технологических процессов используют двойные карты, указывающие как отклонение параметра от нормы, так и его рассеивание. Это могут быть, например, -карты или другие.Таким образом, для определения границ регулирования необходимо знать параметры нормального распределения (математического ожидания)
μ и среднего квадратического отклонения σ.Пример 4.1. В швейном цехе принято решение перевести на статистическое регулирование технологический процесс дублирования деталей. Показателем качества избрана прочность клеевого соединения, равная 8,5 Н/см, и допускаются её отклонения: верхнее отклонение ES= -1,5 Н/см и нижнее - EI= -2,0 Н/см. Построить контрольную -карту и провести статистический анализ процесса.Реализация статистического метода регулирования процесса дублирования осуществляется в три этапа:1- Проводится предварительное исследование состояния процесса и определяется вероятная доля дефектной продукции и коэффициент воспроизводимости.2- Строится контрольная карта и выбирается план контроля.3- Проводится статистическое регулирование процесса дублирования.На первом этапе для проведения исследований необходима информация о процессе. Для испытания отбираем выборку из 100 проб, контроль прочности клеевого соединения проводят через каждый час, при этом испытывают по пять проб, т.е. проводим 20 серий измерений. Результаты контроля - отклонение прочности при расслаивании от установленного показателя качества (8,5Н/см) приведены в табл. 4.3.Таблица 4.3. Результаты контроля - отклонение прочности при расслаивании от установленного показателя качества
По теме «Контрольные карты Шухарта в Statistics Tollbox MATLAB»
Выполнилстудент группы ЗУКд-120Майорова М.С.ПроверилМищенко З. В
Контрольные карты по количественным признакам (табл. 4.1) используются для статистического контроля и регулирования технологического процесса. Регулирование по количественному признаку заключается в определении с требуемой точностью фактических значений контролируемого параметра у выборки продукции. Затем по фактическим значениям контролируемого показателя определяются статистические характеристики процесса и по ним принимаются решения о его состоянии. Таблица 4.1. Виды контрольных карт| Значение характеристики | Название карты | Применение |
| Непрерывные. Регулирование по количественному признаку. |  - карта ( -среднее значение и R - выборочный размах) | Для анализа и управления процессами показатели, качества которых представляют собой непрерывные величины. |
| x - карта медиан (измеряемое значение) | Если группирование данных не эффективно или данные о процессе поступают через большие интервалы. В этом случае данные отдельными точками наносятся на график по мере их поступления. | |
| s- карта – средних квадратичных отклонений | | |
| Дискретные. Регулирование по качественному признаку. | рn-карта числа дефектных единиц продукции | Для контроля числа дефектов при постоянном объеме выборки п. |
| р - карта доли дефектной продук-ции контрольной выборки | При контроле и регулировании технологического процесса. | |
| с - карта числа дефектов | Для числа дефектов в изделиях одинакового размера | |
| и - карта числа дефектов на единицу продукции | Для числа дефектов изделий разного размера | |
Такими характеристиками являются выборочное среднее и медиана (характеристики положения), а также размах и выборочное среднее квадратическое отклонение (характеристики рассеяния случайной величины Х).На контрольную карту наносят значения некоторой статистической характеристики (точки), которые рассчитываются по данным выборок в порядке их получения, верхнюю и нижнюю контрольные границы Кв (или UCL) и Кн (или LCL), верхнюю и нижнюю границы технических допусков Тв и Тн (при их наличии), а также среднюю линию (CL). Иногда используют также предупредительные границы Кп.По количественным признакам используют в основном следующие контрольные карты:- карта средних арифметических значений ( — карта);- карта медиан ( — карта);- карта средних квадратичных отклонений (s -карта);- карта размахов (R -карта).Для – карты и - карты – рассчитывают две границы регулирования или контроля: верхнюю и нижнюю.Для s – карты и R - карты – достаточно рассчитать по одной границе контроля - верхней, так как можно следить лишь за увеличением рассеивания.Карта средних арифметических значений ( 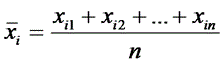—карта) используется для контроля отклонения параметра от нормы и настройки в норму. Точки на контрольной карте — это средние значения небольших выборок, обычно одинакового объема, с 3 до 10 элементов: ,где n — объем выборки (подгруппы).Для получения выборок можно использовать результаты измерений, проводившихся через равные промежутки времени, путем разбиения их на группы.Среднюю линию рассчитывают как среднее из средних значений выборок:
,
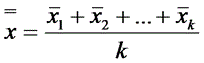
где k — число подгрупп (число точек). Обычно k = 20 … 30.
Контрольные границы рассчитывают по формуле:
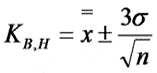, где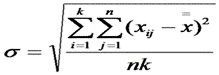 
σ - среднее квадратическое отклонение всей совокупности данных.
В этом выражении (как и при расчете контрольных границ для других видов контрольных карт) коэффициент 3 используется, исходя из правила трех сигм.
Карта медиан (
-карта) используется вместо карты средних значений, когда хотят упростить расчеты. Точки на карте - это медианы выборок одинакового объема с 3 до 10 элементов. Медиана - это при нечетном объеме выборки середина вариативного ряда, при четном объеме выборки - среднее из двух значений середины вариативного ряда.
Средняя линия 
- это среднее из медиан выборок. Контрольные границы определяют по формуле:
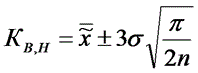
Карта медиан менее точная, чем карта средних значений.
При использовании для расчетов компьютера применения карты медиан вместо карты средних значений вряд ли оправдано.
Карта среднего квадратического отклонения (СКО) (s - карта) используется для контроля рассеяния показателя. Точки на карте - средние квадратические отклонения выборок одинакового объема с 3 до 10 элементов. Средняя линия 
- это среднее по СКО выборок. Контрольные границы:
, 
,
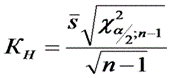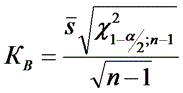где χ2 - критерий Пирсона, n - объем выборки, α - уровень значимости. Обычно принимают α = 0,0027, что соответствует доверительной вероятности 0,9973. Часто на
s - карте используют только верхнюю границу.Карта размахов (R-карта) используется вместо карты средних квадратических отклонений, когда хотят упростить расчеты. При этом карта размахов менее точна.При построении R-карты берут 20…30 выборок одинакового объема от 2 до 10 элементов. Точки на карте - размахи выборок.Размах выборки R — это разность между максимальным xmax и минимальным xmin значениями выборки. Средняя линия - это среднее размахов выборок. Контрольные границы рассчитывают по формулам: , При уровне значимости 0,0027 коэффициенты D3 и D4 можно найти из табл. 4.2. При n <7 нижняя контрольная граница не используется. Таблица 4.2. Значение коэффициентов для R-карты
| N | | | | | | | | | |
| D3 | - | - | - | - | - | 0,076 | 0,136 | 0,184 | 0,223 |
| D4 | 3,267 | 2,575 | 2,282 | 2,115 | 2,004 | 1,924 | 1,864 | 1,816 | 1,777 |
μ и среднего квадратического отклонения σ.Пример 4.1. В швейном цехе принято решение перевести на статистическое регулирование технологический процесс дублирования деталей. Показателем качества избрана прочность клеевого соединения, равная 8,5 Н/см, и допускаются её отклонения: верхнее отклонение ES= -1,5 Н/см и нижнее - EI= -2,0 Н/см. Построить контрольную -карту и провести статистический анализ процесса.Реализация статистического метода регулирования процесса дублирования осуществляется в три этапа:1- Проводится предварительное исследование состояния процесса и определяется вероятная доля дефектной продукции и коэффициент воспроизводимости.2- Строится контрольная карта и выбирается план контроля.3- Проводится статистическое регулирование процесса дублирования.На первом этапе для проведения исследований необходима информация о процессе. Для испытания отбираем выборку из 100 проб, контроль прочности клеевого соединения проводят через каждый час, при этом испытывают по пять проб, т.е. проводим 20 серий измерений. Результаты контроля - отклонение прочности при расслаивании от установленного показателя качества (8,5Н/см) приведены в табл. 4.3.Таблица 4.3. Результаты контроля - отклонение прочности при расслаивании от установленного показателя качества
| Цех швейный | Оборудование — пресс №1 | Контролируемая операция — дублирование | Контроли-руемый параметр - ES= -1,5; 8,5; EI= -2,0 | | | |
| Объем контроля N = 100 | Объем выборки n = 5 | Средство контроля — прочность при расслаивании | | | | |
| Время | № выборки | Результаты контроля - отклонение от показателя качества (8,5) | | | | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 7.00 | | 0,2 | 0,5 | | 0,5 | |
| 8.00 | | 1,5 | | | 1,5 | 1,5 |
| 9.00 | | 1,5 | 1,5 | | | 0,5 |
| 10.00 | | 1,5 | 0,9 | 1,5 | 1,5 | 0,5 |
| 11.00 | | 1,5 | 0,8 | 1,1 | | 0,2 |
| 12.00 | | | 0,5 | 0,6 | 0,1 | 0,3 |
| 13.00 | | 0,2 | 0,5 | | 0,5 | |
| 14.00 | | 1,5 | | | 1,5 | 1,5 |
| 15.00 | | 1,5 | 1,5 | | | 0,5 |
| 16.00 | | 1,5 | 0,9 | 1,5 | 1,5 | 0,5 |
| 7.00 | | 1,5 | 0,8 | 1,1 | | 0,2 |
| 8.00 | | | 0,5 | 1,5 | 0,1 | 0,3 |
| 9.00 | | | 0,5 | | 0,5 | |
| 10.00 | | 1,5 | | | 1,5 | 1,5 |
| 11.00 | | 1,5 | 1,5 | | | 0,5 |
| 12.00 | | 1,5 | 0,7 | 1,5 | 1,5 | 0,5 |
| 13.00 | | 1,5 | 0,8 | 1,1 | | 0,2 |
| 14.00 | | | 0,5 | 0,6 | 0,1 | 0,3 |
| 15.00 | | | 0,5 | | 0,5 | |
| 16.00 | | 1,5 | | | 1,5 | 1,5 |