ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 82
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа № 1
Общий вид задач нелинейного программирования. Графический метод решения задач нелинейного программирования. Метод множителей Лагранжа.
-
Цель работы
Целью лабораторной работы является приобретение студентами практических навыков решения задач линейного программирования графическим методом и использования инструмента Поиск решения среды Excel для нахождения оптимального допустимого решения.
-
Формулировка задачи линейного программирования
Рассмотрим пример с двумя переменными. Компания «Русские краски» производит краску для внутренних и наружных работ из сырья двух типов: М1 и М2 (табл. 1.1).
Таблица 1.1 – Основные данные для задачи

Отдел маркетинга компании ограничил ежедневное производство краски для внутренних работ до 2 тонн, а также поставил условие, чтобы ежедневное производство краски для внутренних работ не превышало более чем на тонну аналогичный показатель производства краски для внешних работ. Компания хочет определить оптимальное соотношение между видами выпускаемой продукции для максимизации общего ежедневного дохода.
-
Математическая модель задачи линейного программирования
Задача линейного программирования, как и любая задача исследования операций, включает три основных элемента.
-
Переменные, которые следует определить; -
Целевая функция, подлежащая оптимизации; -
Ограничения, которым должны удовлетворять переменные.
В нашем примере
необходимо определить ежедневные объемы производства краски для внутренних и наружных работ. Обозначим эти объемы как переменные модели:
x1 – ежедневный объем производства краски для наружных работ;
x2 – ежедневный объем производства краски для внутренних работ.
Используя эти переменные, далее строим целевую функцию Z , как суммарный ежедневный доход, который должен возрастать.
Z 5x1 4x2 .
Ограничения на сырье можно записать следующим образом.
Используемыйобъем
Максимальновозможный

сырьядляпроизводства ежедневный
.
расходсырья


обоихвидовкраски
Из таблицы с данными получим используемые объемы в тоннах:
для сырья для сырья
M1 6x1 4x2 ;
M2 1x1 2x2 .
Поскольку ежедневный расход сырья М1 и М2 ограничен соответственно 24 и 6 тоннами, получаем следующие ограничения.

6x1 4x2 24,
1x1 2x2 6.
Существует еще два ограничения по спросу на готовую продукцию. Первое ограничение указывает, что ежедневный объем производства краски для внутренних работ не должен превышать ежедневный объем производства
краски для наружных работ более чем на одну тонну, т.е.
x2 x1 1. Второе
ограничение максимального ежедневного объема производства краски для
внутренних работ двумя тоннами запишем, как
x2 2 . Учтем условие
неотрицательности переменных:
x1 0, x2 0 .
Окончательно задача будет записана следующим образом:
Z 5x1 4x2 max,
6x1 4x2 24,
x1 2x2 6,


1
x x 1,
2


x
2
2,

x1 0, x2 0.
-
Графический способ решения задачи линейного программирования
Графический способ решения задачи линейного программирования состоит из двух этапов.
-
Построение пространства допустимых решений, удовлетворяющих всем ограничениям модели. -
Поиск оптимального решения среди всех точек пространства допустимых решений.
Этап 1. Построение пространства допустимых решений.
Проведем оси координат. На горизонтальной оси будут указываться
значения переменной
x1, а на вертикальной –
x2 (рис. 1.1). Условия
неотрицательности переменных:
x1 0, x2 0
показывают, что пространство
допустимых решений будет лежать в первом квадранте (т.е. выше оси
x1 и
правее оси
x2 ).
Учтем оставшиеся ограничения, заменив неравенства на равенства и
получив уравнения прямых. Например, неравенство
6x1 4x2 24
заменяется уравнением прямой
6x1 4x2 24 . Найдем две различные точки,
лежащие на этой прямой. При
x1 0, x2 6 . Аналогично для
x2 0, x1 4 .
Проведем искомую прямую через найденные точки (линия 1 на рис. 1.1).
Теперь рассмотрим, как графически интерпретируются неравенства. Точки плоскости, расположенные по одну сторону прямой, удовлетворяют неравенству (допустимое полупространство), а точки, лежащие по другую
сторону, – нет. "Тестовой" точкой, может служить точка 0, 0. Например, эта
точка удовлетворяет первому неравенству
6x1 4x2 24 . Это означает, что
точки полупространства, содержащего начальную точку 0, 0, удовлетворяют этому неравенству. На рис. 1.1 допустимые полупространства показаны стрелочками.
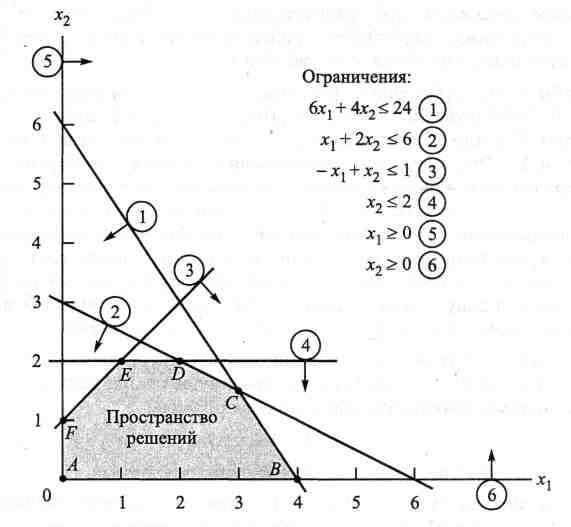
Рисунок 1.1 – Пространство допустимых решений модели
Если точка 0, 0
не удовлетворяет неравенству, допустимым
полупространством будет то, которое не содержит эту точку. Если же прямая проходит через эту точку, следует в качестве "тестовой" взять другую точку.
Этап 2. Поиск оптимального решения.
Точки пространства допустимых решений, показанного на рис. 1.1, удовлетворяют одновременно всем ограничениям. Это пространство ограничено отрезками прямых, которые соединяются в угловых точках А, В, С, D, Е и F. Любая точка, расположенная внутри или на границе области, ограниченной ломаной АВСDЕF, является допустимым решением, т.е. удовлетворяет всем ограничениям. Поскольку пространство допустимых
решений содержит бесконечное число точек, необходима некая процедура поиска оптимального решения.
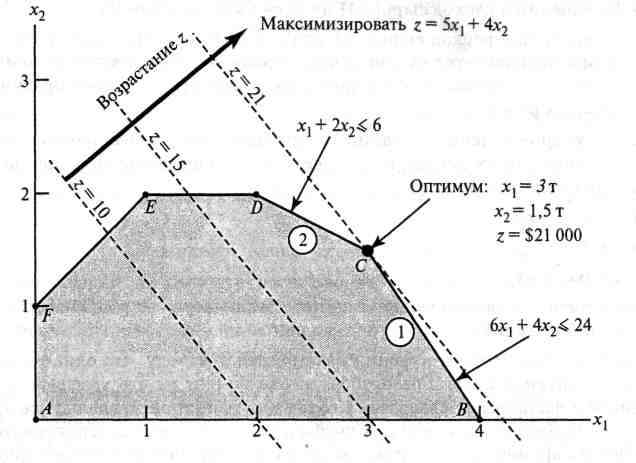
Рисунок 1.2 – Оптимальное значение модели
Для того чтобы найти оптимальное решение, необходимо определить
направление возрастания целевой функции
Z 5x1 4x2 . Мы можем
приравнять Zк нескольким возрастающим значениям, например 10 и 15.
Получаем уравнения прямых
5x1 4x2 10 и
5x1 4x2 15 . На рис. 1.2 эти
прямые показаны штриховыми линиями. Направление возрастания целевой функции отмечено жирной стрелкой. Целевая функция может возрастать до тех пор, пока прямые, соответствующие возрастающим значениям этой функции, пересекают область допустимых решений. Точка пересечения области допустимых решений и прямой, соответствующей максимально возможному значению целевой функции, и будет точкой оптимума.
Оптимальное решение соответствует точке С. Ее координаты