Z 5  3  4 1,5  21. Полученное решение означает, что для компании

«Русские краски» оптимальным выбором будет ежедневное производство 3 тонн краски для наружных работ и 1,5 тонн краски для внутренних работ с ежедневным доходом в 21 000 долл.

5. 
   Использование среды Excel для нахождения оптимального допустимого решения
   

Решение задачи линейного программирования может быть найдено в Excel с помощью инструмента Поиск решения. В верхней части рис. 1.3 показано табличное представление рассматриваемой модели. Здесь содержится 4 типа данных:

1. 
   входные данные (затененные ячейки В5:С9 и F6:F9);
   
2. 
   значения переменных и целевой функции (ячейки в прямоугольнике В13:D13);
   
3. 
   формулы, по которым вычисляются значения целевой функции и левых частей ограничений (ячейки D5:D9);
   
4. 
   поясняющие заголовки и надписи.
   

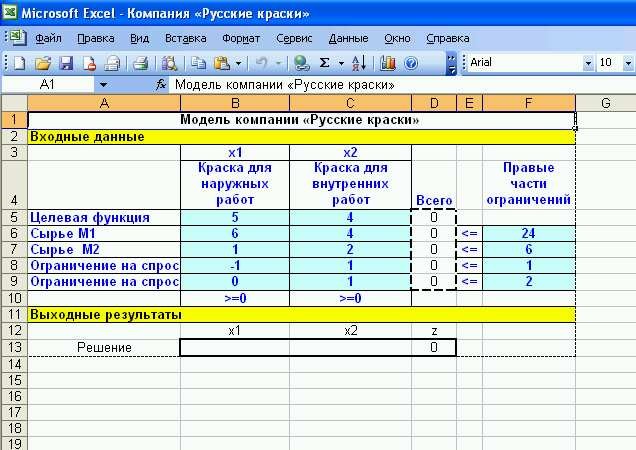
Рисунок 1.3 – Табличное представление задачи в Excel

Поясняющие заголовки и надписи необходимы для того, чтобы сделать табличное представление модели более понятным и удобочитаемым. Относительное расположение ячеек, содержащих информацию разных типов, может быть другим.

Покажем соответствие между математической моделью и табличной. Начнем с соответствия формул этих моделей. Коэффициенты целевой функции и левых частей ограничений помещены в диапазон ячеек В5:С9. В следующей таблице приведены алгебраические формулы и эквивалентные им формулы Excel и ячейки, в которых эти формулы записаны.

---

Формула первоначально вводится только в ячейку D5, а затем ее надо скопировать в ячейки D6:D9. Чтобы правильно скопировать формулы, в формуле ячейки D5 надо ссылки на ячейки В13 и С13 (содержащих значения

x₁ и x₂ ) сделать абсолютными в виде $В$13 и $С$13. Для больших
табличных моделей в ячейку D5 вводят формулу

= СУММПРОИЗВ(В5:С5;$В$13:$С$13)

и затем копируют ее в ячейки D6:D9.

После ввода исходных данных и расчетных формул табличная модель готова для использования средства Поиск решения. В меню Сервис выберите команду Поиск решения. Откроется одноименное диалоговое окно, показанное на рис. 1.4. В этом окне надо ввести адрес ячейки, в которой вычисляется значение целевой функции, указать, надо ли минимизировать или максимизировать целевую функцию, и ввести адреса ячеек, содержащих значения переменных. В нашей модели:

• 
  в поле ввода Установить целевую ячейку вводится $D$5;
  
• 
  устанавливается переключатель Равной максимальному значению;
  
• 
  в поле ввода Изменяя ячейки вводится $В$13:$С$13.
  

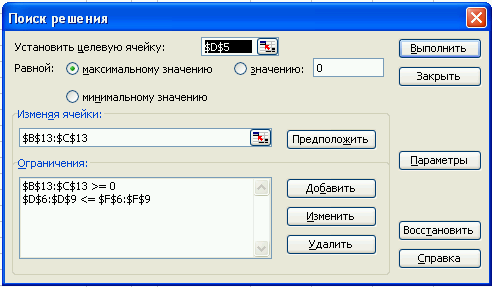
Рисунок 1.4 – Диалоговое окно Поиск решения

Эта информация указывает средству Поиск решения, что переменные находятся в ячейках В13 и С13, и надо найти максимум целевой функции, значение которой вычисляется в ячейке

---

D5.

Далее надо задать ограничения модели, щелкнув на кнопке Добавить в диалоговом окне Поиск решения. Отрывшееся диалоговое окно Добавление ограничения (рис. 1.5), предоставляет средства для ввода всех частей ограничений (левой части, знака неравенства и значения правой части).



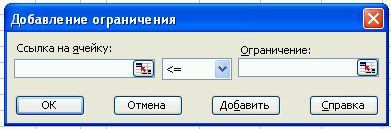
Рисунок 1.5 – Диалоговое окно Добавление ограничения

Используя это окно, вводим ограничения модели в таком виде

$D$6:$D$9<=$F$6:$F$9. В ячейках F6:F9 записаны значения правых частей ограничений. Теперь осталось ввести ограничения неотрицательности для переменных. С помощью диалогового окна Добавление ограничения вводим

$В$13:$С$13>=0

Установка параметров работы средства Поиск решения (максимальное время поиска решения, максимальное количество итераций, относительная погрешность и т.д.), производится в диалоговом окне Параметры поиска решения (рис. 1.6).



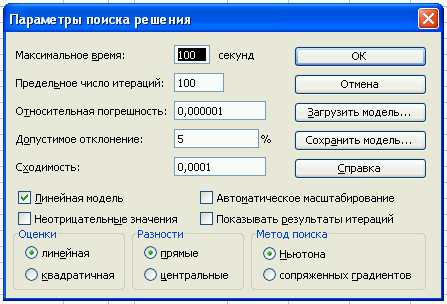
Рисунок 1.6 – Диалоговое окно Параметры поиска решения

Доступ к нему можно получить, щелкнув на кнопке Параметры в диалоговом окне Параметры поиска решения. В этом же окне можно указать требование о неотрицательности всех переменных опцией Неотрицательные значения. Основное условие при решении задачи линейного программирования использование опции Линейная модель.

Для решения задачи, необходимо щелкнуть на кнопке Выполнить в диалоговом окне Поиск решения. Решение появится в выходных ячейках В13:D13 табличной модели (рис. 1.7). Оптимальное значение целевой

---

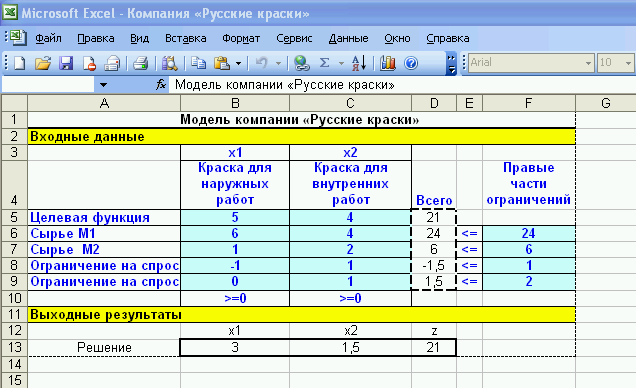
Рисунок 1.7 – Решение задачи в Excel




Рисунок 1.8 – Диалоговое окно Результаты поиска решения

6. 
   Порядок выполнения лабораторной работы
   

1. 
   Получить у преподавателя № задания и выбрать условия задачи в таблице 1.2.
   
2. 
   Решить графическим методом задачу линейного программирования.
   

3. 
   Проверить полученные результаты, найдя оптимальное допустимое решение аналитически, используя табличный редактор Excel.
   
4. 
   Разработать словесную формулировку задачи линейного программирования с двумя переменными и учесть ее при составлении отчета.
   

Таблица 1.2 – Варианты заданий для самостоятельного решения

№	Задача	№	Задача	№	Задача
1	Z 5x1  5x2  max  2x1  x2  2,  x 3x 9,  1 2 x1  x2  3. 	8	Z 2x1  3x2  max  2x1  x2  2, x 3x 9,  1 2 4x1  3x2  24. 	15	Z x1  x2  max  2x1  x2  2,  x 2x 8,  1 2 x1  x2  5. 
2	Z x1  x2  max  3x1  2x2  4,  x 2x 8,  1 2 x x 10,  1 2 4x1  x2  20.	9	Z 5x1  3x2  min 4x1  x2  0,  x x 3,  1 2 2x 3x 6.  1 2	16	Z 2x1  3x2  max x1  3x2  18, 2x x 16,  1 2 x 5,  2 3x1  21.
3	Z 5x1  x2  min 2x1  3x2  0,  5x 9x 45,  1 2 x1  2x2  4. 	10	Z 2x1  3x2  max  6x1  x2  2,  5x 9x 45,  1 2 x1  3x2  3. 	17	Z 4x1  6x2  min 3x1  x2  9, x 2x 8,  1 2 x1  6x2  12. 
4	Z 4x1  2x2  min  3x1  2x2  6, x 2x 10,  1 2 x 3x 6,  1 2 x1  x2  3.	11	Z 2x1  2x2  max  3x1  2x2  4,  x 2x 8,  1 2 x x 20.  1 2	18	Z 3x1  3x2  max 2x1  x2  8, 2x x 1,  1 2 x 2x 2.  1 2
5	Z 3x1  x2  min 4x1  x2  0, 2x x 0,  1 2 x x 3.  1 2	12	Z 2x1  4x2  max  3x1  2x2  6, x 2x 10,  1 2 x 5x 5,  1 2 x1  x2  4.	19	Z 2x1  3x2  1  min x1  x2  4, 2x x 1,  1 2 x 2x 1,  1 2 x1  x2  8.
6	Z x1  x2  max x1  4x2  4  0,  3x1  x2  0, x1  x2  4  0. 	13	Z 2x1  x2  min x1  x2  4,   x1  2x2  2, x1  2x2  10. 	20	Z 5x1  4x2  max 6x1  4x2  24,  x2  2,  x1  x2  0. 
7	Z 2x1  6x2  max x1  x2  2,   x1  2x2  4, x 2x 8.  1 2	14	Z 2x1  x2  min x1  x2  4,  2x1  x2  2,  x 2x 10.  1 2	Для всех задач справедливы неравенства x1  0, x 0.  2

---

Метод Лагранжа.

Составить математическую модель задачи. Для расчёта модели использовать метод множителей Лагранжа.

Мукомольный комбинат реализует муку двумя способами: в розницу через магазин и оптом через торговых агентов. При продаже х_{ кг муки через магазин расходы на реализацию составляют   ден. ед., а при продаже x₂ кг муки посредством торговых агентов —   ден. ед. Определить, сколько кг муки следует продавать каждым способом, чтобы затраты на реализацию были минимальными, если в сутки для продажи выделяется 5000 кг муки.

Решение. Составим математическую модель задачи. Найдем минимум суммарных расходов



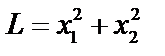
при ограничениях:

х_{ + х₂ = 5000,

Для расчета модели используем метод множителей Лагранжа. Составим функцию Лагранжа.

Найдем частные производные функции F по х₁, х₂ и λ, приравняем к нулю, получим систему уравнений:



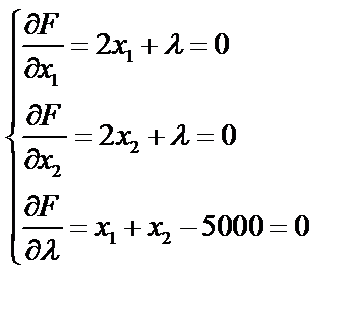
Из первого и второго уравнений имеем x₁ – x₂ =0.

Решая это уравнение совместно с третьим, имеем λ = -5000, х₁ = 2500, х₂ = 2500, L=12 500 тыс. ден. ед. Давая х₁ значения больше и меньше 2500 находим L и из определения экстремума функции получаем, что L при х₁ = х₂ = 2500 достигает ми­нимума.

Ответ. Для получения минимальных расходов необходимо расходо­вать в сутки через магазин и торговых агентов по 2500 кг муки, при этом расходы на реализацию составят 12 500 тыс. ден. ед.

I вариант решения в Exsel

Переменные:	x1	x2	Значение ЦФ
Значения переменных
Коэффициенты Ц.Ф.			Значения огр-ний
Коэффициенты ограничений:

---

Смотрите также файлы

• Реферат Инкурабельді пациент. Паллиативті кмекті этикалы сратары араанды 2022 Жоспар.docx

• Q в трубе диаметром d 1 150 мм, имеющей плавное сужение до диаметра d 2 75 мм, если показания пьезометров до сужения h 1 90 см в сужении h 2 70 см. Температура воды 260 С. Решение.doc

• На какие вопросы отвечают Сколько я сэкономил.pptx

• Нужно выполнить и отправить на проверку своему учителю с помощью.pdf

• Контрольная работа Бобкова Олеся Сергеевна Группа м 106 Специальность Менеджмент.doc