Файл: Выполнение практических заданий по дисциплине математические методы в психологии.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 26.10.2023

Просмотров: 145

Скачиваний: 11

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Автономная некоммерческая организация высшего образования

«МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления
Форма обучения: заочная


ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

Математические методы в психологии



Группа

Студент
Т.В. Миронова


МОСКВА 2022

Задания к практической работе 1.

Определение числовых характеристик.

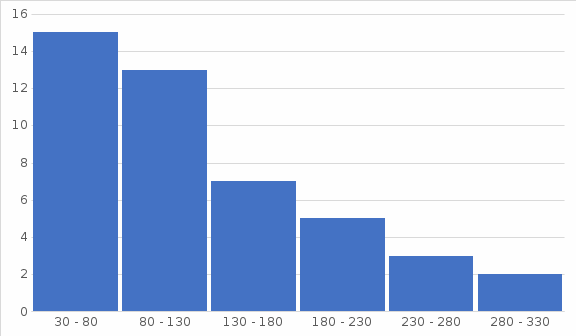
Задание 1. Проведено выборочное обследование частных психологических кабинетов города. Имеются следующие данные о величине посещаемости для 50 кабинетов города ( 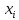– количество клиентов в месяц, млн. руб.; 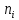– число кабинетов).



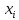30 - 80
80 - 130
130 - 180
180 - 230
230 - 280
280 - 330



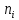15
13
7
5
3
2

Найти:

а) среднее 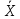, среднеквадратичное отклонение 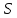и коэффициент ;

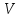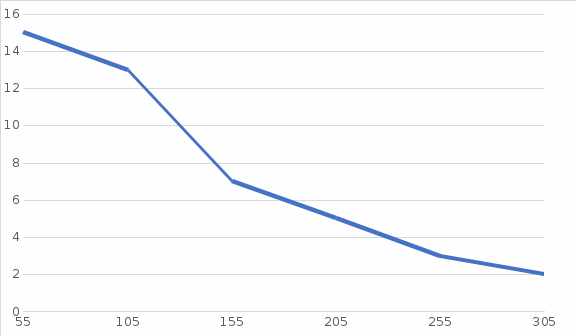
б) построить гистограмму и полигон частот.

а) Для вычисления выборочных характеристик каждый интервал представляем его серединой 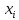. Заполняем расчётную таблицу.












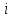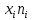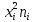1
55
15
825
45375

2
105
13
1365
143325

3
155
7
1085
168175

4
205
5
1025
210125

5
255
3
765
195075

6
305
2
610
186050

∑



45
5675
948125

Объём выборки равен сумме всех частот : .

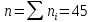Выборочное среднее вычисляем по формуле средней арифметической взвешенной (веса - частоты):



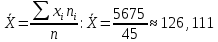
Выборочное среднее представляет собой несмещённую оценку математического ожидания случайной величины 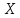– посещаемость психологических кабинетов города.

Выборочную дисперсию вычисляем по формуле:



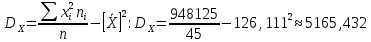
Выборочная дисперсия является смещённой оценкой дисперсии случайной величины 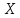. Несмещённой оценкой является исправленная выборочная дисперсия: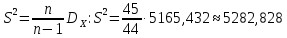



Среднеквадратичное отклонение
(исправленное):

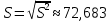
Коэффициент вариации равен отношению среднеквадратичного отклонения к среднему: .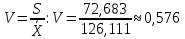

Полученное значение больше 0,33 (33%), значит степень колеблемости рассматриваемого признака велика, совокупность неоднородная.

б) Для построения гистограммы частот по оси абсцисс откладываем интервалы, на них как на основаниях строим прямоугольники высотой .







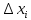
Для построения полигона частот соединяем ломаной линией точки с координатами 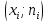. Здесь – середины интервалов.









Задание 2. Из генеральной совокупности извлечена выборка объема
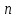
. Найти среднее значение, дисперсию, среднее квадратическое отклонение, исправленную дисперсию, коэффициент вариации, моду и медиану.
9,5
10
10,5
11
11,5
12
12,5



3
15
30
15
5
4
2

Заполняем расчётную таблицу.








1
9,5
3
28,5
270,75

2
10
15
150
1500

3
10,5
30
315
3307,5

4
11
15
165
1815

5
11,5
5
57,5
661,25

6
12
4
48
576

7
12,5
2
25
312,5

∑



74
789
8443

Объём выборки равен сумме всех частот : 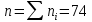. Среднее значение вычисляем по формуле средней арифметической взвешенной (веса - частоты):



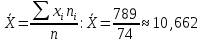
Выборочное среднее представляет собой несмещённую оценку математического ожидания случайной величины .

Выборочную дисперсию вычисляем по формуле:



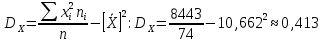
Среднее квадратическое отклонение:

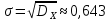
Выборочная дисперсия является смещённой оценкой дисперсии случайной величины . Несмещённой оценкой является исправленная выборочная дисперсия:



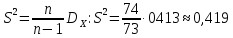
Среднеквадратичное отклонение (исправленное):

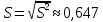
Коэффициент вариации равен отношению среднеквадратичного отклонения к среднему: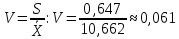



Полученное значение незначительно отличатся от нуля, значит степень колеблемости низкая, совокупность однородная.

Мода – значение признака с максимальной частотой: видим, что максимальная частота 30 – у :



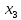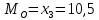
Для определения медианы вычисляем накопленные частоты. То значение , на котором впервые накопленная частота превышаем половину объёма выборки (у нас 74/2 = 37), представляет медиану (серединное значение).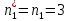







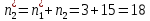
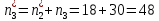
Значение 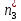впервые превысило 37, значит медиана: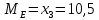



Задание 3. Дан следующий вариационный ряд:
1
2
3
4
5
6
7
8
9
10



2
2
3
3
5
5
5
6
6
6

Смотрите также файлы