Требуется: 1) Построить полигон распределения.2) Вычислить выборочную среднюю, дисперсию, моду, медиану.1) Сначала построим статистический ряд (ряд распределения): для каждого принимаемого значения исследуемогопризнака подсчитываем частоты – сколько раз в выборке встречается это значение.

	2	3	5	6
	2	2	3	3

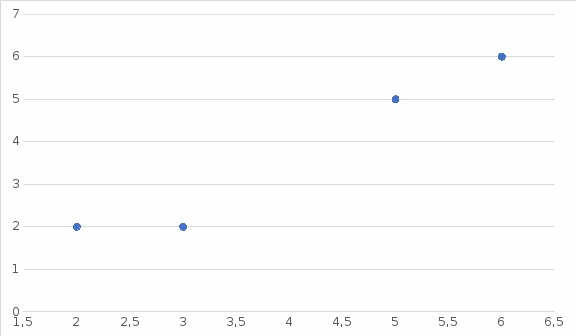
Для построения полигона распределения соединяем ломаной линией точки с координатами . 2) Объём выборки равен сумме всех частот : 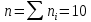. Выборочное среднее вычисляем по формуле средней арифметической взвешенной: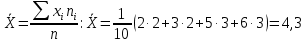

---

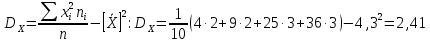
Дисперсию вычисляем по формуле:Мода – значение признака с максимальной частотой: видим, что максимальная частота 3 – у двух значений 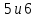, значит есть две моды (бимодальное распределение): 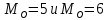.Для определения медианы вычисляем накопленные частоты. То значение , на котором впервые накопленная частота превышаем половину объёма выборки (у нас 10/2 = 5), представляет медиану (серединное значение).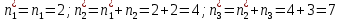Значение впервые превысило 5, значит медиана: 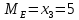.Задания к практической работе 2.Статистическая обработка данных.Задание 1. У 24 девушек – студентов физического и психологического факультетов был измерен уровень вербального интеллекта по методике Векслера. Можно ли утверждать, что одна из групп превосходит другую по уровню вербального интеллекта? Физики: 123, 134, 126, 131, 134, 132, 126, 132, 127, 127, 136, 133, 136, 135, Психологи: 123, 125, 132, 120, 127, 126, 120, 126, 120, 119.Поскольку в одной из выборок число значений меньше 11, то критерий Q Розенбаума использовать нельзя. Используем критерий U – критерий Манна-Уитни.Упорядочим значения в обеих выборках (по убыванию) и вычисляем ранги. При совпадении значений используем связные ранги.

Физики	Ранг	Психологи	Ранг
136	23,5
136	23,5
135	22
134	20,5
134	20,5
133	19
132	17	132	17
132	17
131	15
127	13	127	13
127	13
126	9,5	126	9,5
126	9,5	126	9,5
		125	7
123	5,5	123	5,5
		120	4
		120	3
		120	2
		119	1
Сумма	228,5		71,5

---

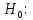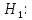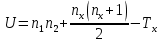
Видим по сумме рангов, что в группе студентов-физиков уровень вербального интеллекта выше. Тогда формулируем гипотезы: Студенты-физики не превосходят студентов-психологов по уровню вербального интеллекта. 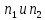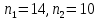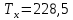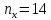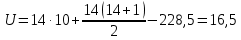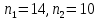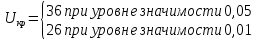Студенты-физики превосходят студентов-психологов по уровню вербального интеллекта.Определяем значение U по формуле:Здесь – количество испытуемых в группе 1 и группе 2 соответственно, ; – большая из двух ранговых сумм; – количество испытуемых в группе с большей суммой рангов.Определяем критические значения для :Поскольку 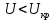, то гипотеза 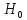отклоняется и принимается альтернативная гипотеза 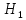. Значит, можно считать, что студенты-физики превосходят студентов-психологов по уровню вербального интеллекта.Задание 3. Психолог просит супругов проранжировать девять личностных черт, имеющих определяющее значение для семейного благополучия. Задача заключается в том, чтобы определить, в какой степени совпадают оценки супругов по отношению к ранжируемым качествам. Заполните таблицу и, посчитав коэффициент ранговой корреляции Спирмена, ответьте на поставленный вопрос.

Черты личности	№	Муж	Жена
Ответственность	1	3	1
Общительность	2	9	8
Сдержанность	3	2	4
Выносливость	4	8	5
Жизнерадостность	5	4	7
Терпеливость	6	5	6
Решительность	7	6	3
Оптимизм	8	7	9
Надёжность	9	1	2

---

Рассчитваем коэффициент ранговой корреляции Спирмена.Составляем расчётную таблицу.

Ранг	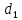Ранг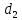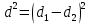
3	1	4
9	8	1
2	4	4
8	5	9
4	7	9
5	6	1
6	3	9
7	9	4
1	2	1

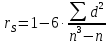
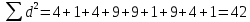
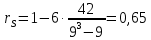
По формуле вычисляем коэффициент ранговой корреляции Спирмена.Формулируем гипотезы: Корреляция между оценками супругов не значима (не отличается от нуля) Корреляция между оценками супругов значимаПо таблице находим критические значения коэффициента корреляции для значения 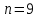при уровне значимости 0,05: 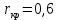.Поскольку 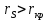, то гипотеза отклоняется: можно считать, что оценки супругов по отношению к ранжируемым качествам отличаются значимо.Заметим, что при уровне значимости 0,01 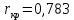, на этом уровне значимости выполнялось бы 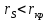и в этом случае гипотеза была бы принята:

---

тогда можно было бы считать, что оценки супругов по отношению к ранжируемым качествам отличаются незначительно.

---

Смотрите также файлы

• Absorption costing как метод поглощаемых издержек основан на разделении общих валовых издержек (ТС).docx

• Задачи Задача Дайте оценку динамики выпуска.doc

• 1 Испытуемый 1 Отчёт.docx

• Какое трудовое законодательство распространяется на Потапову.doc

• Линией электропередач. Электрические сети могут быть выполнены воздушными и кабельными линиями, шинопроводами и токопроводами. Кабельная линия электропередачи (КЛ).docx