Расчет простейшего эжектора

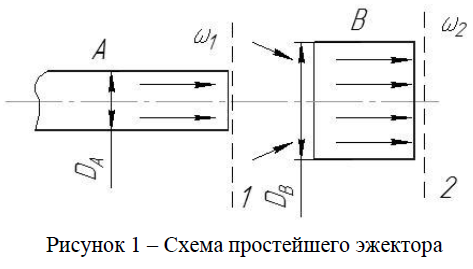
Провести расчет простейшего эжектора, состоящего из канала А и цилиндрического насадка В. Схема эжектора представлена на рисунке 1.


Определить скорость w2 и массовый расход жидкости на выходе из эжектора (сечение 2).

Дано:

Температура окружающей жидкости и жидкости в канале А: 25 оС

Давление окружающей среды: 0,1 МПа

Рабочее тело (жидкость): вода

Плотность жидкости: 1000 кг/м3

При расчете принимаются следующие допущения:

– силами трения о стенки эжектора пренебречь;

– вследствие малых скоростей жидкости считать плотность жидкости величиной постоянной;

– скорость жидкости в пространстве вокруг эжектора равна 0 м/с.

D_A=16 мм, D_В=26 мм, w₁ = 3 м/с.

Решение:

Построим контрольную поверхность из сечений 1 и 2, проходящих нормально к потоку по срезу канала А, смесительной камеры В и боковых поверхностей, направленных параллельно потоку. На всей полученной контрольной поверхности примерно одно и то же давление, равное давлению окружающей среды, т. е. главный вектор сил давления равен нулю.

Пренебрегая силами трения, сумма проекций на ось трубы всех сил в пределах контрольной поверхности 1–2 равна нулю, следовательно, количество движения не меняется.

Изменение количества движения у активной струи на участке 1–2 равно:



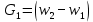
Количество движения жидкости, подсосанной из окружающего пространства, где она находилась в покое (w = 0):



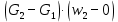
Суммарное изменение количества движения:



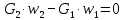
где G₁, G₂ – секундные массовые расходы жидкости, соответственно в сопле и на выходе из смесительной трубы;

w₁, w₂ – значения скорости истечения из сопла и смесительной трубы:

Отсюда получаем, что расходы жидкости в сопле и на выходе из смесительной трубы обратно пропорциональны величинам соответствующих скоростей:

---

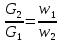
С другой стороны, отношение расходов жидкости можно записать как:


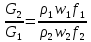
где 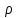– плотность; f – площадь сечения.

Сравнивая последние два выражения, приходим к следующей расчетной формуле:



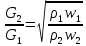
В нашем случае плотность жидкости в активной струе и окружающем пространстве одинакова, следовательно, отношение массовых расчетов жидкости равно отношению диаметров смесительной трубы и сопла:



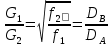
Подставляя значения диаметров, найдем отношение расходов:


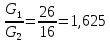
Далее определим скорость жидкости на выходе из эжектора:



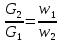
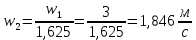
И наконец, определим расход жидкости на выходе:




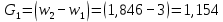
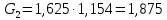
Задача 2. Определение расхода воздуха через канал с конфузорно-диффузорной вставкой
Произвести обработку экспериментальных данных, определим расход воздуха через два канала, и определим, на сколько отличается расход воздуха через один канал по отношению к расходу через другой канал, построим график зависимости расхода воздуха от перепада давлений.

Решение:

Для определения расхода воздуха G (кг/с) применим формулу:



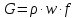
где 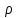– это плотность воздуха в критическом сечении измеряемого сопла, кг/м³;

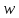- – это скорость воздуха в критическом сечении сопла, м/с;

- f – площадь критического сечения сопла, м².

Для вычисления расхода воздуха необходимо вычислить площадь критического сечения:

---

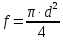
где d = 0,012 м – диаметр сопла в критическом сечении, м:



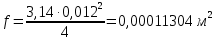
Находим плотность и скорость воздуха через газодинамические функции.

1. 
   Определим приведенное давление по формуле:
   

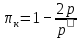
где р – измеренное давление в критическом состоянии сопла (по ртутному манометру), мм рт.ст;

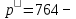давление окружающей среды, замеренное по барометру, мм рт.ст.
По формуле:



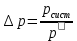
из которой следует:



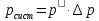
Данные вычислений и результаты расчетов сведем в таблицу 1

2. 
   Определяем температуру воздуха в критическом сечении мерного сопла Т, К:
   

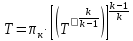
где 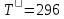- температура окружающей среды, К;

k =1,4 показатель адиабаты для воздуха.

Рассчитаем температуру воздуха, данные сведем в таблицу 1.

3. 
   Определяем число Маха М по формуле:
   

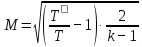
Результаты вычислений сведем в таблицу 1.

4. 
   Определяем скорость звука а, м/с, по формуле:
   

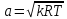
где R = 287 Дж/кг·К – газовая постоянная для воздуха.

Все значения сведем также в таблицу 1.

5. 
   Определяем скорость воздуха в критическом сечении w, м/с по формуле:
   

6. 
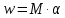
   Из уравнения состояния находим плотность окружающей среды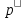 , кг/м³, по формуле:
   

7. 
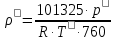
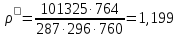
   Определяем плотность воздуха в критическом сечении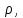 кг/м³, по формуле:
   

---

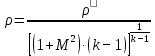
Результаты вычислений заносим в таблицу 1

8. 
   Определяем массовый расход воздуха G, кг/с, по формуле:
   

Таблица 1

3		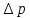0,94	0,92	0,9	0,88	0,86	0,84	0,82	0,8	0,78	0,75	0,7
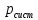		43	57	72	83	94	103	113	124	133	146	170
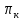		0,89	0,85	0,81	0,78	0,75	0,73	0,7	0,68	0,65	0,62	0,55
	Т	265	253	241.1	232	223	217	208	202	193	185	164
	М	0,76	0,92	1,07	1,17	1,28	1,35	1,45	1,53	1,63	1,73	2,01
	а	326	319	311	305	299	295	289	285	278	273	257
	w	248	293	333	357	383	398	419	438	453	472	517
		3,75	2,56	1,76	1,37	1,05	0,89	0,7	0,58	0,46	0,37	0,21
	G	0,105	0,084	0,066	0,055	0,045	0,04	0,033	0,029	0,024	0,019	0,012
4		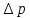0,94	0,92	0,9	0,88	0,86	0,84	0,82	0,8	0,78	0,75	0,7
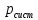		30	39	50	63	73	86	100	111	123	140	170
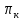		0,92	0,9	0,87	0,84	0,81	0,77	0,74	0,71	0,68	0,63	0,55
	Т	274	268	259	250	241	229	220	211	202	188	164
	М	0,63	0,72	0,85	0,96	1,07	1,21	1,31	1,42	1,53	1,69	2,01
	а	332	328	323	317	311	303	297	291	285	275	257
	w	209	236	275	304	333	367	389	413	436	465	517
		5,15	4,18	3,04	2,31	1,76	1,24	0,97	0,75	0,58	0,41	0,21
	G	0,122	0,112	0,095	0,079	0,066	0,051	0,043	0,035	0,029	0,022	0,012

---

9. 
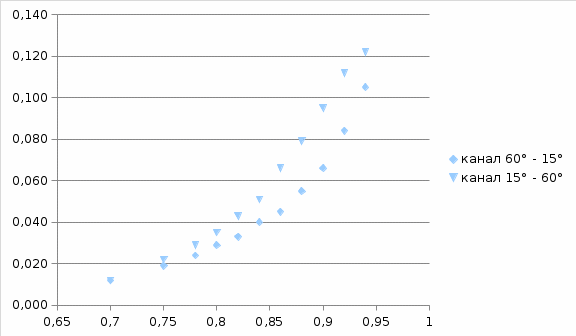
   По полученным значениям расхода воздуха строим график зависимости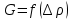 через каналы 3,4.
   

---

Смотрите также файлы

• Криминалистическое оружиеведение.docx

• Выполнение практических заданий по дисциплине математические методы в психологии.docx

• Absorption costing как метод поглощаемых издержек основан на разделении общих валовых издержек (ТС).docx

• Задачи Задача Дайте оценку динамики выпуска.doc

• 1 Испытуемый 1 Отчёт.docx