ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 11
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Программа среднего профессионального образования
44.02.01 Дошкольное образование
Дисциплина: Математика
Практическое занятие 2
Выполнил:
Обучающийся Селиверстова Ольга Сергеевна
Преподаватель:
Сазонова Элеонора Борисовна
Задание 1. (Максимальное количество баллов – 3 балла)
| Задача | Модель | Интерпретация модели |
| 1. Было 7 кубиков, проиграно 4 кубика. Сколько кубиков осталось? | | Известно:начальное состояние обьекта;направленность отношения между начальным и конечным состоянием обьекта;числовое значение величины отношения между состоянием объекта. Необходимо определить:числовое значение величины конечного состояния объекта. |
| Было 4 кубика, стало 7 кубиков. Что произошло? | | Известно:начальное и конечное состояние обьекта;направленность отношения между ними. Необходимо определить:характер и числовое значение величины отношений между состояниями объектов. |
| 3. Имеется 7 кубиков после того, как добавили 4 кубика. Сколько кубиков было до добавления | | Известно:значение величины конечного состояния объекта, направленность отношений между состояниями объекта и числовое значение величины отношений между состояниями объектов. Необходимо определить:числовое значение величины начального состояния объекта. |
| 4.Было 7 кубиков, стало 4 кубика. Что произошло? | | Известно:значение величины начального и конечного состояния объекта, направленность отношений между состоянием объекта. Необходимо определить:числовое значение величины отношений между состояниями объектов. |
| 5.В первый раз принесли 7 кубиков, во второй раз – забрали 4 кубика. Что произошло в результате? | | Известно:направленность отношений между состояниями обьекта:числовое значение величин отношений между ними, состояние обьекта(начального, промежуточного и конечного) Необходимо определить:значение величины отношений между навальным и конечным состояниями объекта. |
| 6. В первый раз забрали 7 кубиков, во второй – принесли 4 кубика. Что произошло в результате? | | Извесно:направленность отношений между состояниями обьекта;числовое значение величин отношений между состояниями объекта. Необходимо определить:значение величины отношения между навальным и конечным состоянием объекта. |
| 7.В первый раз забрали 4 кубика. После того, как кубики забрали второй раз, всего было отдано 7 кубиков. Что произошло во второй раз? | | Известно:направленность отношений между состояниями обьекта:числовое значение величин отношений между состояниями объекта. Необходимо определить:значение велечены отношений между начальные и конечным состоянием объекта. |
| 8. В первый раз забрали 7 кубиков. После того, как во второй раз принесли кубики, оказалось, что всего было отдано 4 кубика. Что произошло во второй раз? | | Известно:направленность отношений между состояниями обьекта;значение величин отношений между начальные и промежуточные, между промежуточные и конечном состоянием объекта. Необходимо определить:определить отношение между промежуточные и конечным состоянием объекта. |
Задание 2. (Максимальное количество баллов – 3 балла)
Ответ:
1) не желают водить детей в кружки – 40% родителей
2) выбрали не менее двух кружков – 60% родителей
Задание 3.
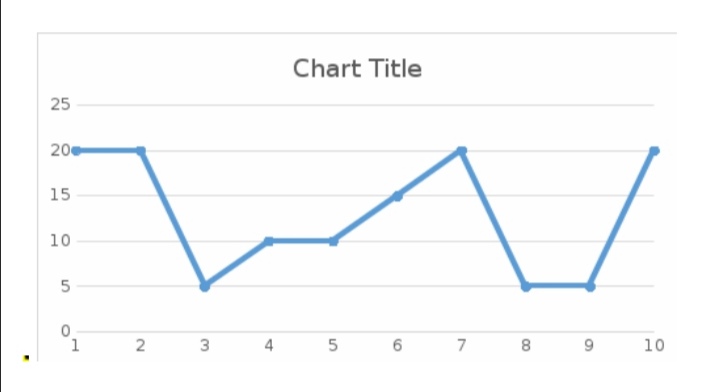
Номер измерения:
5
6
7
8
9
Данные
10
15
20
5
5
Мо= 5*10+6*15+7*20+8*5+9*5 = 365 = 6,6…
55 55
Ответ: Мо=7
Ме: 55- нечетное , Расположим числа в порядке возрастания: 5 5 10 15 20
Так как количество чисел равно 5, а это нечетное число, то найдем медиану как значение среднего элемента 10
Ответ: Ме=10
d) Построить выборочную функцию распределения.
Задание 4 (максимальное количество баллов - 4 балла)
Округлить число 4,45575250 до шести, пяти, четырех, трех, двух и одного десятичных знаков; до целого числа.
4,45575250 до шести знаков = 4,455753
4,45575250 до пяти знаков = 4,45575
4,45575250 до четырёх знаков = 4,4558
4,45575250 до трех знаков = 4,456
4,45575250 до двух знаков = 4,46
4,45575250 до одного знака = 4,5
4,45575250 до целого числа = 4
-
Число 12,75 определено с относительной погрешностью 0,3, %. Найдите абсолютную погрешность округления.
Округляя число 12,75 получаем 12,8. Прибавляем 1 к десятым, потому что сотые больше 5.
Абсолютная погрешность равна модулю разницы между точным и округленным числом, 12,8 – 12,75 = 0,05
Относительная погрешность равна абсолютной, деленной на приближенное значение, выраженное в процентах, 0,05 / 12,8 * 100% = 0,003%
c) Определите верные и сомнительные цифры числа 13,27 ± 0,03.
Определение: «Цифра называется верной, если граница абсолютной погрешности данного приближенного значение числа не больше единицы того ряда, в котором записана эта цифра. В противном случае цифра называется сомнительной».
х = 13,75 ± 0,03
0,03 - граница абсолютной погрешности
Единица последнего разряда - 0,01 (сотые)
0,03 > 0,01
значит цифра 5 - сомнительная
0,03 < 0, 1 - значит цифра 2 - верная
Если в записи приближенного значения числа какая-то цифра – верная, то и все предшествующие ей цифры так же являются верными.
Значит 3; 1 - также верные цифры
В записи приближенного значения числа сохраняют только верные цифры, а сомнительные цифры округляют, значит
х = 13,3
Задание 5 (максимальное количество баллов – 3 балла)
На стороне AC треугольника ABC отмечена точка D так, что AD=3см, DC=10см. Площадь треугольника ABC равна 39 см2. Найдите площадь треугольника ABD.
Дано: треугольник ABC, AD=3см, DC=10см, S треугольника ABC=39 см2.
Найти: S треугольника ABD
Решение:
BH – общая высота, следовательно SABC/SABD = AC/AD
39/SABD = 13/3
13 SABD = 39*3
SABD = 39*3/13 = 9
Ответ: 9 см2
.
Задание 6 (максимальное количество баллов – 4 балла)
Биссектриса угла A параллелограмма ABCD пересекает его сторону BC в точке F. Найдите площадь параллелограмма ABCD, если BF=4 см, FC=2 см, а угол ABC равен 1500.
Ответ:
Дано: параллелограмм ABCD, BF=4 см, FC=2 см, ABC=1500.
Найти: S параллелограмма ABCD
Решение: Накрест лежащие углы BFA и FAD равны, AF— биссектриса BAD, следовательно, BFA и FAD = BAF
Значит, треугольник BFA равнобедренный и AB=BF=4
По формуле площади параллелограмма находим:
Ответ: 14
Задание 7 (максимальное количество баллов – 3 балла)
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6см и 8см, а боковое ребро призмы равно 12см
Решение:
Сторона ромба a выражается через его диагонали и формулой
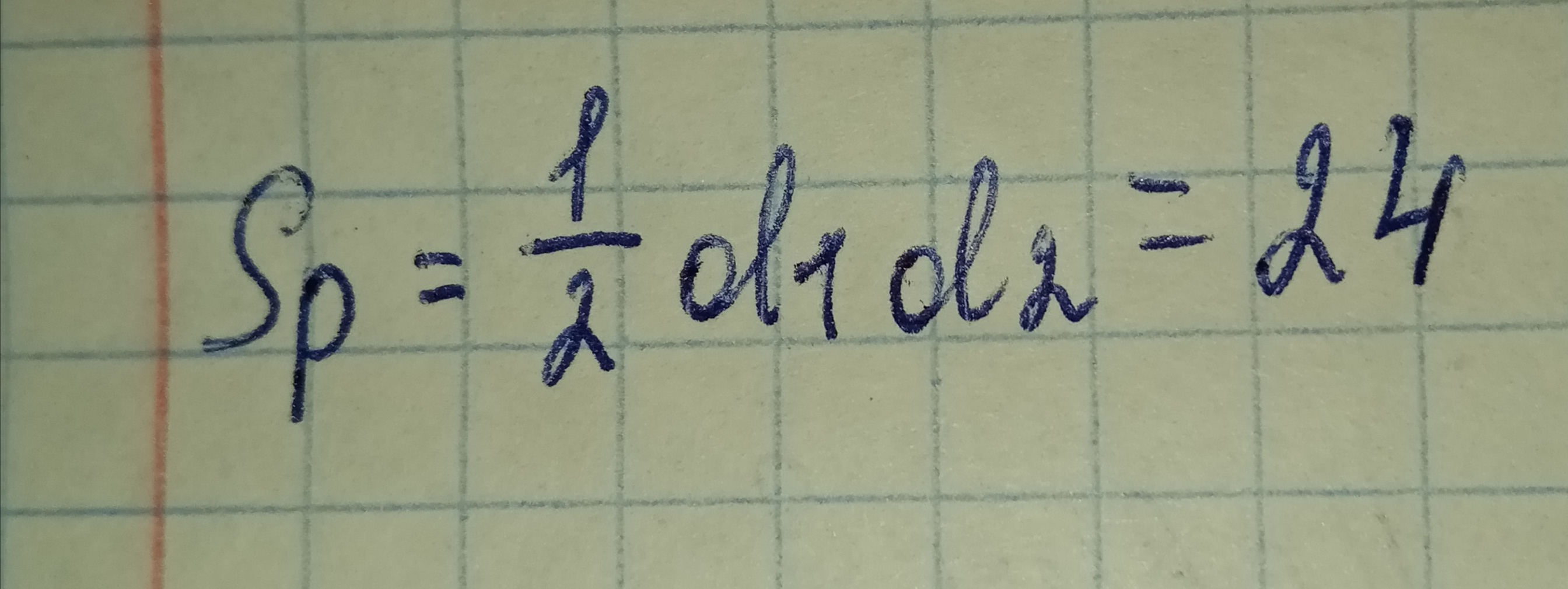
Найдем площадь ромба
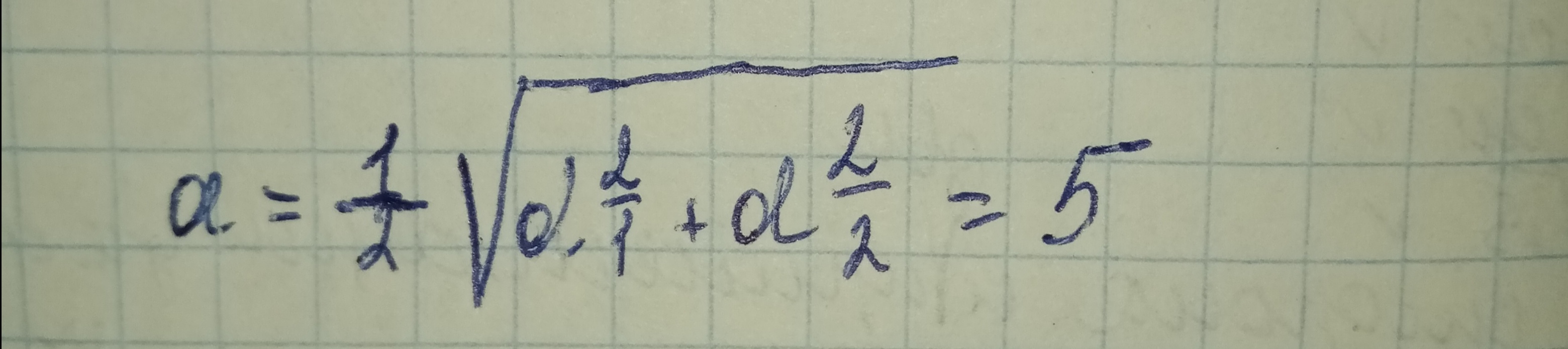
Тогда площадь поверхности призмы равна:
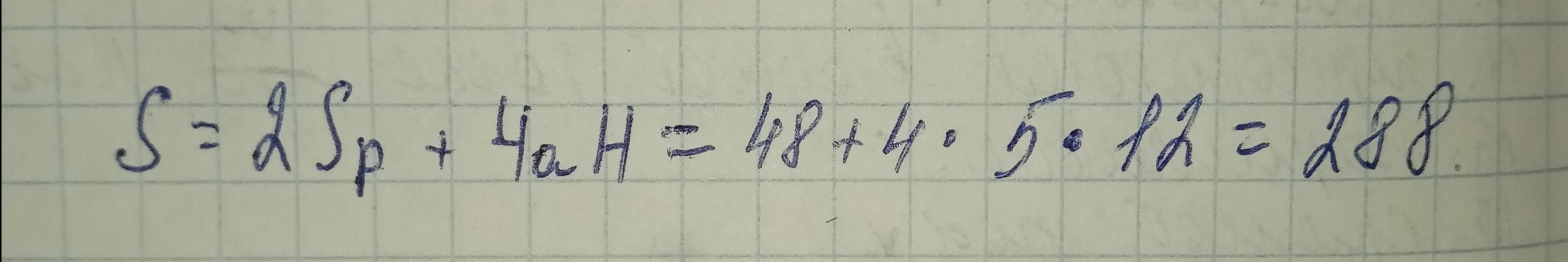
Ответ: 288.