Файл: Оценка надёжности по.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 26.10.2023

Просмотров: 787

Скачиваний: 17

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическая работа Факторы, определяющие надежность ИСМодель Миллса. Простая интуитивная модельЦель работы: научиться оценивать надежность ПС.Практическая частьЗадачи по теме «Оценка надёжности ПО» Модель Миллса.Задача 1.Предположим в программе 12 собственных ошибки, внесём ещё 6 случайным обра­зом. В процессе тестирования было найдено 7 ошибок из рассеянных и 5 собственные. Найти надёжность по модели Миллса.N= (S*n)/V= (6*5)/7= 4.28C= S/S+k+1= 6/ 7+12+1= 0.3 Задача 2.Предположим в программе перед началом тестирования было 90 ошибок. Искусст­венно рассеяно 20 ошибок. 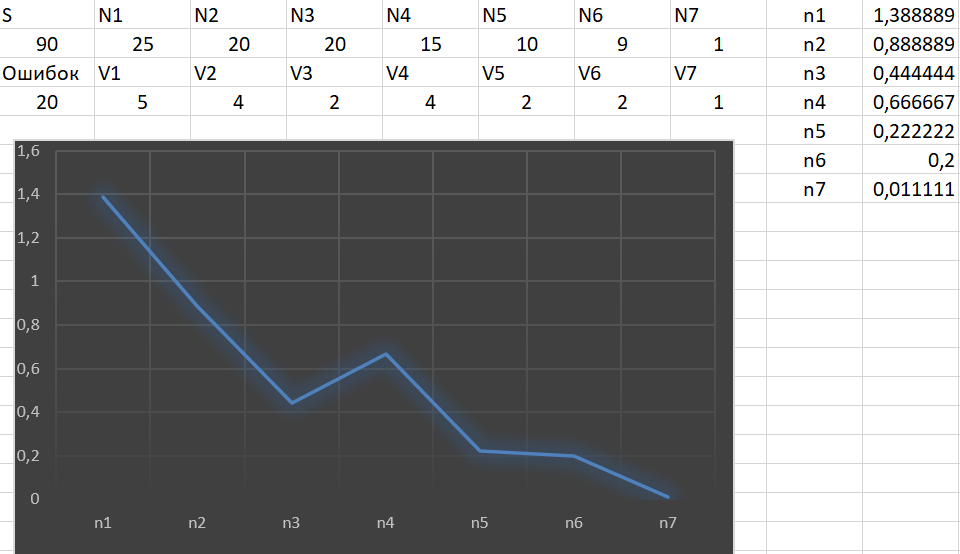В процессе тестовых прогонов было выявлено следующее ко­личество ошибок:N 25 20 20 15 10 9 1V 5 4 2 4 2 2 1Рисунок 1 – задача 2Оценить число возможно оставшихся ошибок в программе после каждого тестово­го прогона. Меру доверия к модели оценить после последнего прогона (С – ?). Построить график зависимости возможного числа ошибок от № прогона.Задача 3.Предположим в программе перед началом тестирования было 100 ошибок. Искус­ственно рассеяно 15 ошибок. 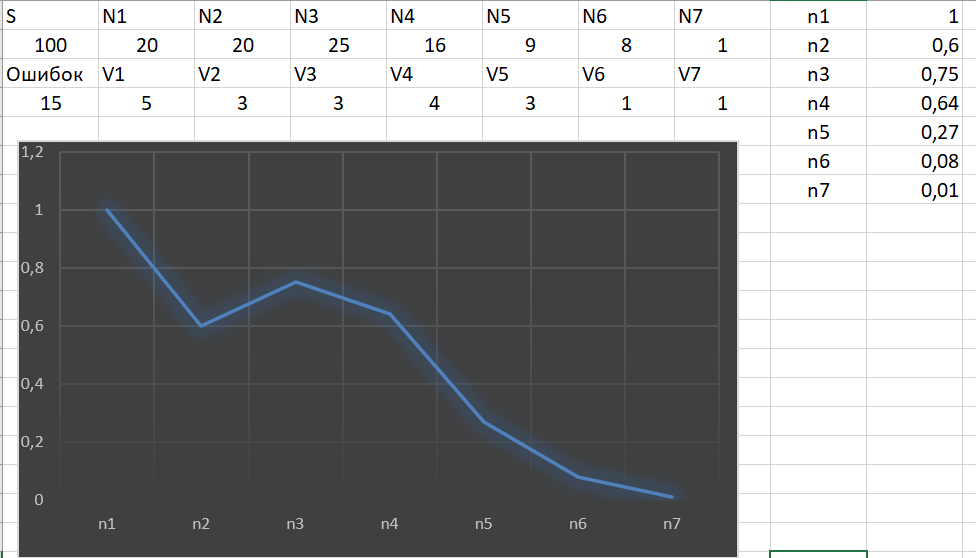В процессе тестовых прогонов было выявлено следующее количество ошибок:N 20 20 25 16 9 8 1V 5 3 3 4 3 1 1Рисунок 2 – задача 3Оценит число возможно оставшихся ошибок в программе после каждого тестового прогона. Меру доверия к модели оценить после последнего прогона (С – ?). Построить график зависимости возможного числа ошибок от № прогона.Задача 4.Предположим в программе перед началом тестирования было 80 ошибок. Искусст­венно рассеяно 30 ошибок. 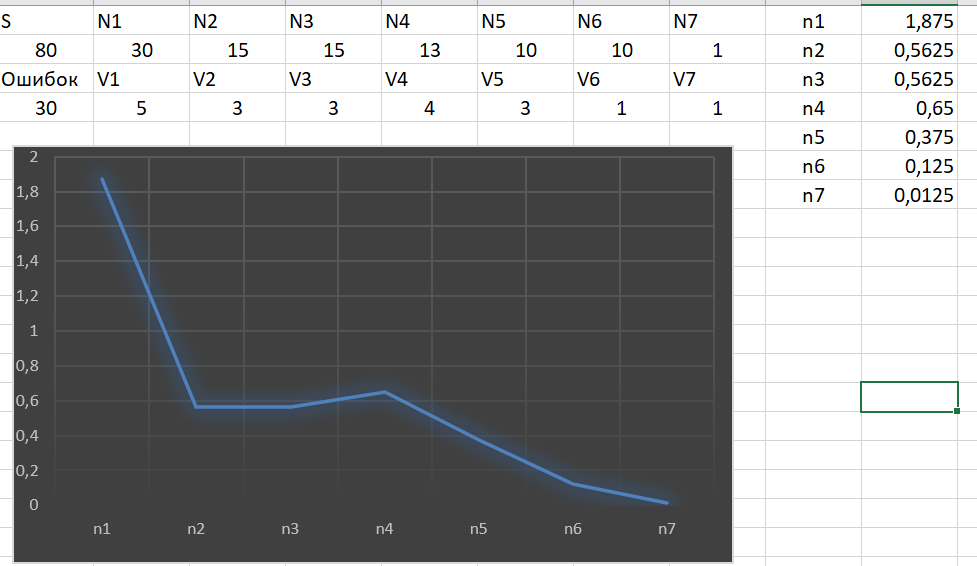В процессе тестовых прогонов было выявлено следующее ко­личество ошибок:N 30 15 15 13 10 10 1V 5 3 3 4 3 1 1Рисунок 3 – задача 4Оценит число возможно оставшихся ошибок в программе после каждого тестового прогона. Меру доверия к модели оценить после последнего прогона (С – ?). Построить график зависимости возможного числа ошибок от № прогона.
Простая интуитивная модель.Задача 1.В процессе тестирования программы 1-я группа нашла 15 ошибок, 2-я группа на­шла 25 ошибок, общих ошибок было 5. Определить надёжность по простой интуитивной модели.N=15*25/5=75E1=15/75=0.2E2=25/75=0.33Задача 2.В процессе тестирования программы 1-я группа нашла 5 ошибок, 2-я группа нашла 2 ошибки, общих ошибок было 2. Определить надёжность по простой интуитивной модели.N1-5 n2-2 obh-2 N=5*2/2=5 E1=5/5=1 E2=2/5=0,4Задача 3.В процессе тестирования программы 1-я группа нашла 35 ошибок, 2-я группа на­шла 25 ошибки, общих ошибок было 20. Определить надёжность по простой интуитив­ной модели.N= 35*25/20= 43.75E1= 35/43.75= 0.8E2= 25/43.75=0.57Задача 4.В процессе тестирования программы 1-я группа нашла 5 ошибок, 2-я группа нашла 40 ошибок, общих ошибок было 5. Определить надёжность по простой интуи­тивной модели.N1-5 N2-40 OBH-5N=5*40/5=40 E1=5/40=0,125 E2=1Контрольные вопросы

  1. Дайте определение сложности программного средства.
представляет неотъемлемое свойство программирования и программ, которое проявляется во времени и стоимости создания программ, в объеме или длине текста программ, характеристиках ее логической структуры, задаваемой операторами передачи управления (ветвления, циклы, вызовы подпрограмм и т.д.).

  1. Приведите классификацию динамических МНПС.
подразделяются на аналитические и эмпирические. Аналитические модели дают возможность рассчитать количественные показатели надежности, основываясь на данных о поведении программы в процессе тестирования (измеряющие и оценивающие модели). Эмпирические модели базируются на анализе структурных особенностей программ. Они рассматривают зависимость показателей надежности от числа межмодульных связей, количества циклов в модулях, отношения количества прямолинейных участков программы к количеству точек ветвления и т.д. Часто эмпирические модели не дают конечных результатов показателей надежности, однако они включены в классификационную схему

, так как развитие этих моделей позволяет выявлять взаимосвязь между сложностью ПС и его надежностью. Эти модели можно использовать на этапе проектирования ПС, когда осуществлена разбивка на модули и известна его структура.

Смотрите также файлы