ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 31
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Определить тип дифференциального уравнения
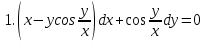
Данная функция может быть записана как:
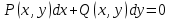
Соответственно, тип данного уравнения – уравнение в полных дифференциалах
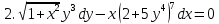
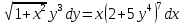
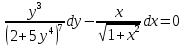
Данная функция может быть записана как:
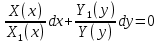
Где
Соответственно, тип данного уравнения – уравнение с разделяющими переменными
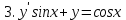
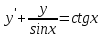
Данная функция может быть записана как:
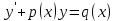
Соответственно, тип данного уравнения – линейное дифференциальное уравнение
2. Найти общее решение дифференциального уравнения
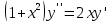
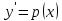
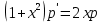
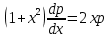
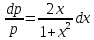
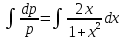
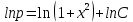
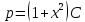
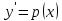
Интегрируя полученное уравнение еще раз, находим функцию
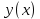
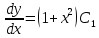
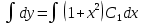
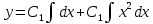
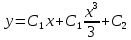
3. Найти решение уравнения, удовлетворяющее начальному условию
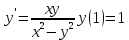
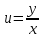
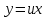
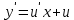
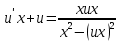
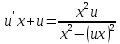
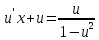
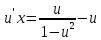
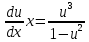
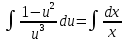
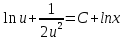
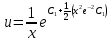
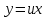
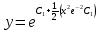
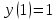
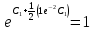
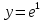частное решение 4. Найти общее решение дифференциального уравнения
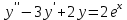
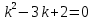
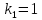
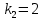
Общее решение дифференциального уравнения:
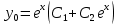
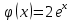
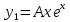
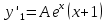
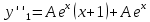
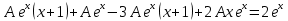
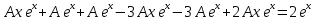
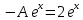
Откуда
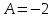
Частное решение:
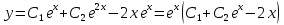
5. Записать вид учн для дифференциального уравнения:
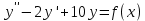
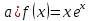
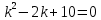
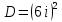
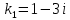
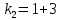
Общее решение дифференциального уравнения:
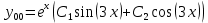
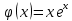
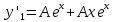
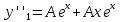
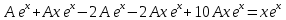
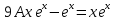
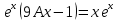
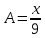
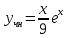
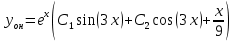
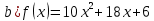
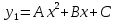
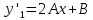
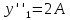
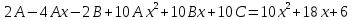
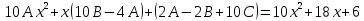
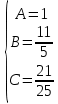
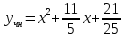
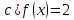
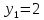
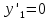
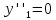
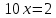
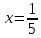
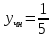
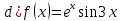
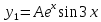
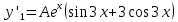
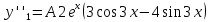
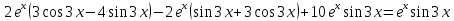
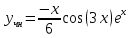
6. Найти решение дифференциального уравнения
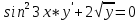, удовлетворяющее начальному условию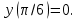
Вычислить значение решения задачи Коши при
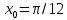
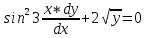
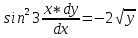
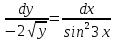
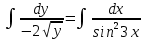
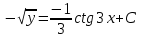
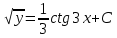
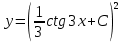
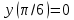
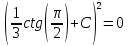
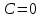
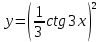- решение дифференциального уравнения, удовлетворяющее начальному условию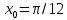 
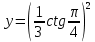
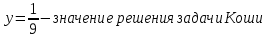
7. Найти решение дифференциального уравнения
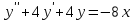, удовлетворяющее начальным условиям 
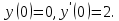Вычислить значение решения задачи Коши при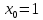 
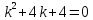
Общее решение дифференциального уравнения:
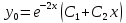
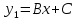
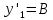
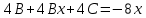
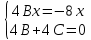
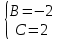
Частное решение:
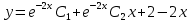
y(0)=0
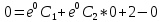
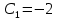
Находим первую производную:
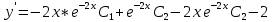
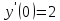
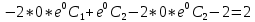
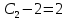
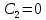
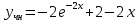
значение решения задачи Коши при
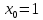
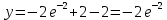
8. Найти область сходимости степенного ряда
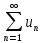, где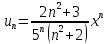 
Областью сходимости степенного ряда является интервал (-R;R), где:
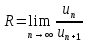
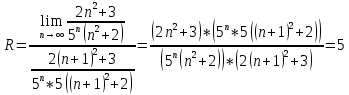
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (-5;5)