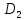ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 32
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Теперь проверим сходимость ряда на концах этого интервала.
Пусть
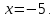Получаем ряд: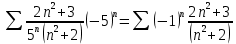
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие не выполняется
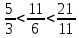
б) Предел ряда должен стремится к 0.
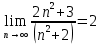
Данное условие не выполняется.
Ряд расходится, значит,
- точка расходимости.При
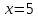. получаем ряд: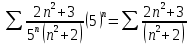
числовой знакоположительный ряд.
Исследуем его сходимость при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл:
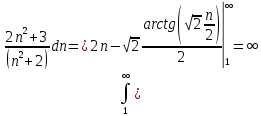
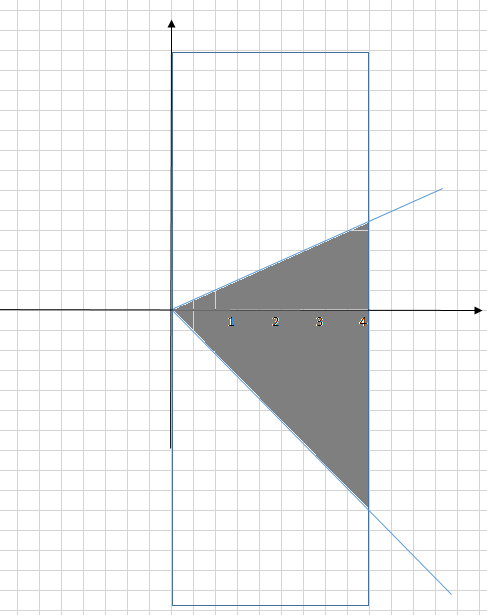
Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Значит, x = 5 - точка расходимости.
Таким образом, данный степенной ряд является сходящимся
Область сходимости:
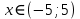
9. Вычислить определенный интеграл
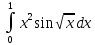с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно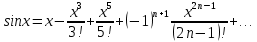
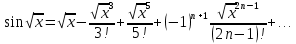
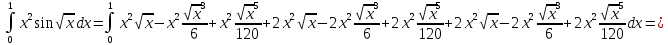
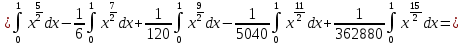
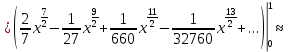
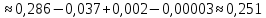
Четвертый член этого знакочередующегося ряда по модулю меньше 0,001, поэтому для вычисления интеграл с точностью до 0,001достаточно взять сумму первых трех членов ряда, при этом допускаем ошибку
10. Разложить функцию
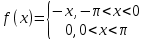в ряд Фурье в интервале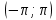 
1.
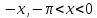
Разложение в ряд Фурье на интервале(
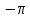;0) имеет вид: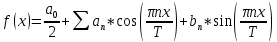 
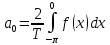
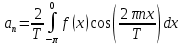
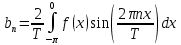
Для наших данных:
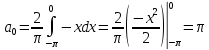
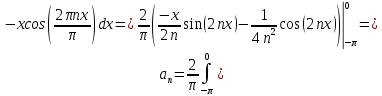
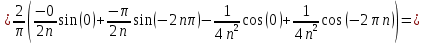
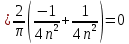
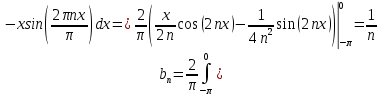
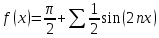
11. Найти
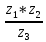в показательной и тригонометрической формах, если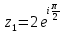 
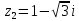
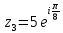
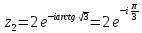
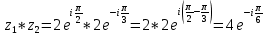
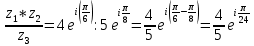
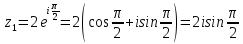
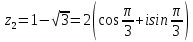
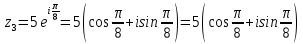
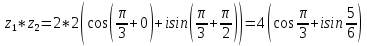
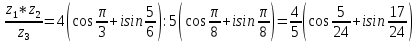
12. Найти мнимую часть числа
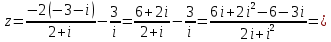
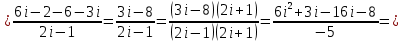
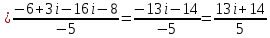
13. Построить области
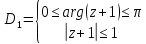
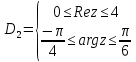
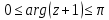– сектор круга с центром 1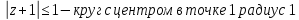
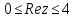– полоса 
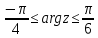сектор круга с центром 0Область
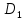
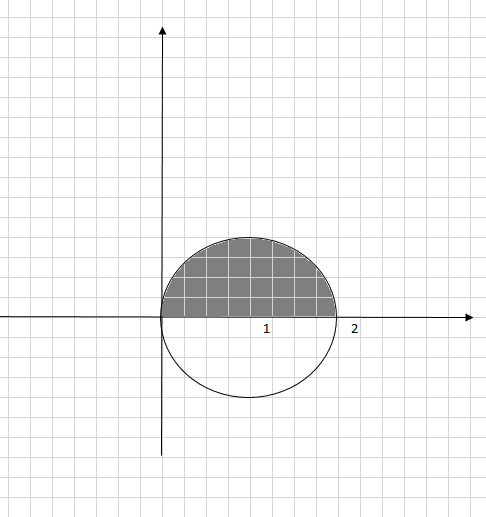
Область
