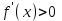ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.10.2023
Просмотров: 28
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Элементы математического анализа
Пусть x0, х две точки из области определения функции y = f(x). При переходе из точки x0 в точку х значение функции меняется с f(x0) на f(x).
Величина х = х - x0 называется приращением аргумента.
Величина y = f(x) - f(x0) называется приращением функции.
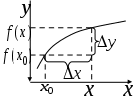
Производной функции y = f(x) в точке х0 называется предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю, если этот предел существует
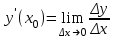 .
.Обозначение:
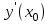 ,
, 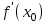
Процесс нахождения производной называется дифференцированием. Функция, дифференцируемая во всех точках некоторого промежутка, называется дифференцируемой на этом промежутке. Учитывая это, можно опустить индекс «0» у величины х0, и записывать производную как
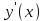 или
или 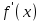 , где х – произвольная точка.
, где х – произвольная точка.Правила дифференцирования
1) Производная от постоянной равна нулю,
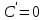 .
.2) Производная от независимой переменной равна единице,
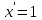 .
.3) Если u = u(x), v = v(x) дифференцируемые функции, то
a)
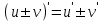
b)
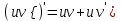
c)
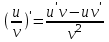
Следствие. Постоянный множитель можно вынести за знак производной, т.е.
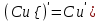
Таблица производных
| 1 | 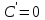 , С- const , С- const | 6 | 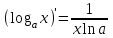 | 11 | 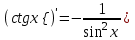 |
| 2 | 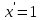 | 7 | 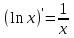 | 12 | 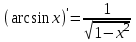 |
| 3 | 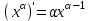 | 8 | 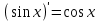 | 13 | 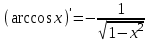 |
| 4 | 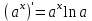 | 9 | 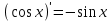 | 14 | 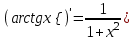 |
| 5 | 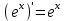 | 10 | 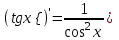 | 15 | 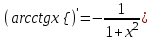 |
Запомнить:
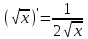 ,
, 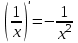
Упр. Вычислить производные
1)
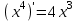 ; 2)
; 2) 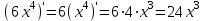
3)
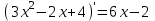 ; 4)
; 4) 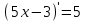 ; 5)
; 5) 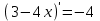
6)
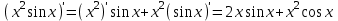
7)
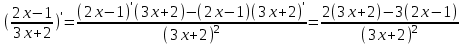 =
==
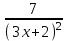 .
.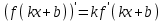
1)
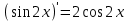 ; 2)
; 2) 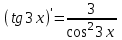
3)
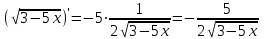
4)
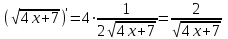
5)
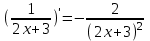 ; 6)
; 6) 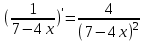
7)
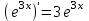 ; 8)
; 8) 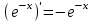
13)
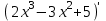 ; 14)
; 14) 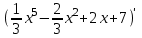
Упр.
1) Найти производную функцию f(x) в точке x0
a) f(x) = x2 + x + 1, x0 = 1
▼
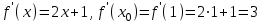 ▲
▲b) f(x) = x - 3x2, x0 = 2
▼
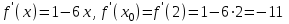 ▲
▲2) При каких значениях х производная функции
f(x) = (x – 1)(x – 2)(x – 3) равна 11
▼ f(x) = (x – 1)(x – 2)(x – 3) = x3 – 6x2 + 11x - 6
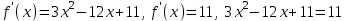
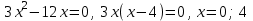 Отв. х = 0; 4▲
Отв. х = 0; 4▲3) При каких значениях х производная функции
f(x) = 3x4 – 4х3 - 12х2 + 3 принимает положительные значения
▼
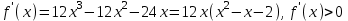
x(x2 – x – 2) > 0
x = 0; -1; 2
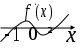
Отв. х =
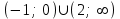 ▲
▲Производная сложной функции
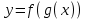 ,
, 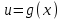
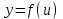 ,
, 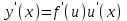
Упр. Вычислить производные.
1)
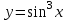 , u = sinx
, u = sinxy = u3,
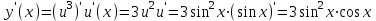
2)
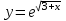 ,
, 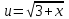
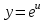 ,
, 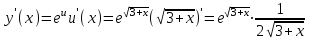
3)
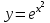 , u = x2,
, u = x2, 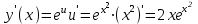
4)
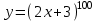 . u = 2x + 3,
. u = 2x + 3, 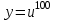 ,
, 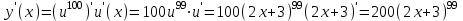
5)
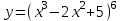 . u = x3 – 2x2 + 5, y = u6
. u = x3 – 2x2 + 5, y = u6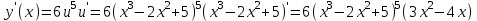
6)
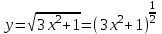 ,
, 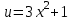 ,
, 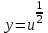
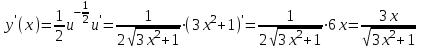
7)
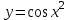 , u = x2
, u = x2y = cosu,
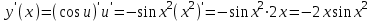
8)
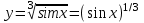 , u = sinx, y = u1/3
, u = sinx, y = u1/3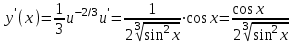
9)
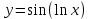 , u = lnx, y = sinu
, u = lnx, y = sinu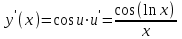
Геометрический смысл производной
Производная функции f(x) в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке, т.е.
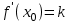 , где k = tg - угловой коэффициент касательной.
, где k = tg - угловой коэффициент касательной.Свойства tg
1) тангенс острого угла положителен;
2) тангенс тупого угла отрицателен;
3) большему углу соответствует большее значение тангенса угла.
Упр.
1) Найти тангенс угла наклона касательной, проведенной к графику функции y = 3x2 - 6x + 4 в точке x = 2
▼
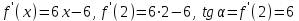 ▲
▲2) Найти угловой коэффициент касательной к графику функции y = 1/x + 4 в точке x = 1/2
▼
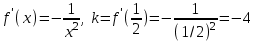 ▲
▲Уравнение касательной к кривой
Запишем уравнение прямой, проходящей через точку М0(х0,у0).
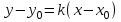 ,
,где k– угловой коэффициент прямой.
Положив
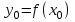 ,
, 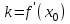 , получим
, получим 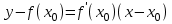 , или
, или 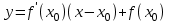 - уравнение касательной к кривой
- уравнение касательной к кривой 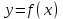 в точке х0.
в точке х0.Упр.
1) Найти уравнение касательной к графику функции f(x) = x2 + 2x в точке х = 2.
▼
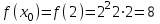 ,
, 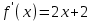 ,
, 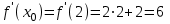 , тогда
, тогда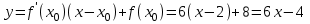 , y = 6x – 4 – уравнение касательной ▲
, y = 6x – 4 – уравнение касательной ▲2) Найти уравнение касательной к графику функции
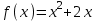 , параллельной прямой y = 4x - 5.
, параллельной прямой y = 4x - 5.▼ У прямой y = 4x – 5 угловой коэффициент k = 4.
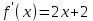 . Из условия параллельности
. Из условия параллельности 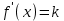 находим точку касания х0, т.е. 2х + 2 = 4, х = 1.
находим точку касания х0, т.е. 2х + 2 = 4, х = 1.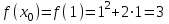
,
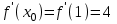
Составляем уравнение касательной

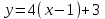 ,
, 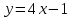 ▲
▲3) Найти уравнение касательной к графику функции
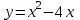 , параллельной оси абсцисс.
, параллельной оси абсцисс.▼
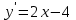 . Из условия
. Из условия 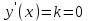 находим точку касания х0, т.е. 2х + 4 = 0, х = 2.
находим точку касания х0, т.е. 2х + 4 = 0, х = 2.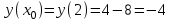 ,
, 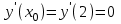
Составляем уравнение касательной
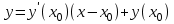
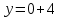 ,
, 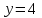 ▲
▲5) Укажите точку графика функции
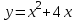 , в которой касательная параллельна прямой y - 2x + 5 = 0.
, в которой касательная параллельна прямой y - 2x + 5 = 0.▼ Запишем уравнение прямой в виде
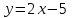 , где k = 2 – угловой коэффициент прямой. Искомая точка касания х0 находится из условия:
, где k = 2 – угловой коэффициент прямой. Искомая точка касания х0 находится из условия: 
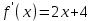 ,
, 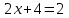 , х = -1,
, х = -1, 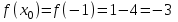
Точка касания (x0, f(x0)) = (-1; -3). ▲
Признаки возрастания и убывания функции
Если во всех точках некоторого промежутка:
а)
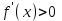 , то функция f(x) возрастает на этом промежутке;
, то функция f(x) возрастает на этом промежутке;б)
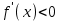 , то функция f(x) убывает на этом промежутке.
, то функция f(x) убывает на этом промежутке.1) Найти область возрастания функции
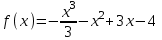
▼ Обл. опр.
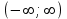 .
.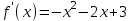 ,
,