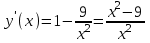ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.10.2023
Просмотров: 29
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- условие возрастания функции f(x).
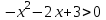 ,
,
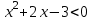
x = -3; 1
Область возрастания: (-3; 1), или [-3; 1] ▲
Экстремум функции
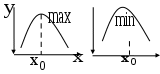
Точка х0 называется точкой максимума (минимума) функции f(x), если для всех х из некоторой окрестности этой точки выполняются неравенства
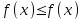 , то х0 – точка максимума;
, то х0 – точка максимума;
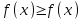 , то х0 – точка минимума.
, то х0 – точка минимума.
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках называются экстремумами функции.
Необходимые условия экстремума
Если функция y = f(x) имеет экстремум в точке х0, лежащий внутри области определения функции, то ее производная либо равна нулю, либо не существует.
либо равна нулю, либо не существует.
Производная функции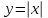 в точке х = 0 не существует, но экстремум в этой точке есть.
в точке х = 0 не существует, но экстремум в этой точке есть.
Точки, в которых выполнены необходимые условия экстремума, называются критическими точками.
Замечание. Если в какой-то точке имеется экстремум, то эта точка критическая; обратно неверно, т.е. критическая точка не обязательно является точкой экстремума. Критическая точка должна входить в область определения функции.
Например, рассмотрим функцию y = x3.
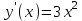 ,
, 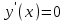 x= 0 – критическая точка, но экстремума нет.
x= 0 – критическая точка, но экстремума нет.
Упр. Найти критические точки.
1)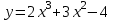 . Обл. опр.: (-; ).
. Обл. опр.: (-; ).
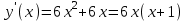 ,
, 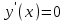 ,
, 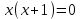
x = 0; -1 – критические точки.
2)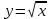 . Обл. опр.: 0; )
. Обл. опр.: 0; )
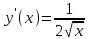 ,
,  не существует при х = 0, но эта точка не лежит внутри области определения, следовательно, не есть критическая точка.
не существует при х = 0, но эта точка не лежит внутри области определения, следовательно, не есть критическая точка.
Вывод: Экстремума нет, поскольку не критических точек.
3)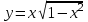 . Обл. опр.: -1; 1
. Обл. опр.: -1; 1
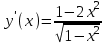 ,
,  при
при 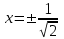 - критические точки, т.к. лежат внутри области определения функции.
- критические точки, т.к. лежат внутри области определения функции.
 не существует при х = 1, но не критические точки, поскольку не лежат внутри области определения функции.
не существует при х = 1, но не критические точки, поскольку не лежат внутри области определения функции.
4)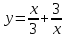 . Обл. опр.: (-; 0)U(0; )
. Обл. опр.: (-; 0)U(0; )
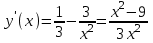 ,
,
 при
при 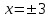 - критические точки, т.к. лежат внутри области определения функции.
- критические точки, т.к. лежат внутри области определения функции.
 не существует при х = 0, но не критические точки, поскольку не лежит внутри области определения функции.
не существует при х = 0, но не критические точки, поскольку не лежит внутри области определения функции.
5)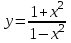 . Обл. опр.: (-; -1)U(-1; 1) U(1; )
. Обл. опр.: (-; -1)U(-1; 1) U(1; )
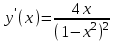 ,
,  при
при 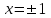 - критическая точки.
- критическая точки.
 не существует при х = 0, но не критические точки, поскольку не лежит внутри области определения функции.
не существует при х = 0, но не критические точки, поскольку не лежит внутри области определения функции.
6)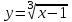 . Обл. опр.: (-; )
. Обл. опр.: (-; )
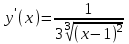 ,
,  не существует при х = 1- критическая точка.
не существует при х = 1- критическая точка.
Достаточное условие экстремума


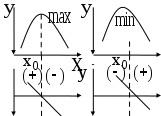
Если при переходе через критическую точку производная функции меняет знак с плюса на минус, то имеет место максимум функции, а если с минуса на плюс – минимум. Если же знак производной не меняется, то экстремума нет.
Замечание. Факт возрастания функции будем обозначать стрелкой вверх , а убывание – стрелкой вниз
, а убывание – стрелкой вниз 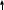 , тогда
, тогда
Схема исследования функции на экстремум и
области возрастания и убывания функции
1) Найти производную .
.
2) Найти критические точки, которые лежат внутри области определения функции.
3) Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремума функции и области возрастания и убывания функции.
4) Найти экстремум функции.
Замечание. Критические точки отделяют область возрастания и область убывания функции.
Упр. Найти экстремумы и области возрастания и убывания функции.
1)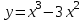 . Обл. опр.: (-; );
. Обл. опр.: (-; );
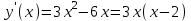 ;
;
 х = 0; 2- критические точки. Наносим все критические точки на числовой прямой. Критические точки разбивают числовую ось на три области.
х = 0; 2- критические точки. Наносим все критические точки на числовой прямой. Критические точки разбивают числовую ось на три области.
Для определения знака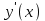 в каждой области используются следующие способы.
в каждой области используются следующие способы.
а) Прямой способ. Возьмем контрольные точки в окрестности каждой критической точки и определим знак производной в контрольной точке.
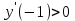 ,
, 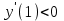 ,
, 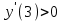
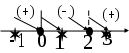
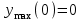 ,
, 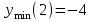
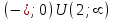 - область возрастания функции;
- область возрастания функции;
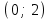 - область убывания функции.
- область убывания функции.
б) Нанесем график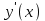

Корни: х = 0; 2

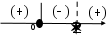
в) Метод интервалов.
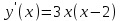 - стандартный вид
- стандартный вид
Корни: х = 0; 2
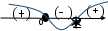
2)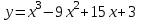 . Обл. опр.: (-; );
. Обл. опр.: (-; ); 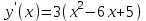 ;
;
 х = 1; 5- критические точки.
х = 1; 5- критические точки.
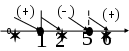
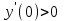 ,
, 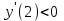 ,
, 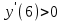
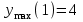 ,
, 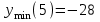
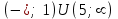 - область возрастания функции;
- область возрастания функции;
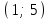
- область убывания функции.
3)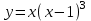 . Обл. опр.: (-; );
. Обл. опр.: (-; ); 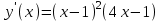 ;
;
 х = 1; 1/4- критические точки.
х = 1; 1/4- критические точки.
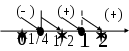
 ,
,  ,
, 
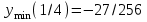
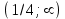 - область возрастания функции;
- область возрастания функции;
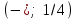 - область убывания функции.
- область убывания функции.
4)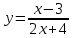 . Обл. опр.: (-;-2)U(-2; );
. Обл. опр.: (-;-2)U(-2; ); 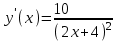 ;
;
 не существует при х = -2, которая не лежит внутри области определения функции, т.е. не критическая точка, следовательно, экстремума нет.
не существует при х = -2, которая не лежит внутри области определения функции, т.е. не критическая точка, следовательно, экстремума нет.
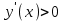 при всех х -2, следовательно,
при всех х -2, следовательно, 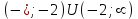 - область возрастания функции.
- область возрастания функции.
5)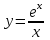 . Обл. опр.: (-; 0)U(0; );
. Обл. опр.: (-; 0)U(0; ); 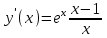 ;
;
 х = 1- критическая точка.
х = 1- критическая точка.
 не существует при х = 0, которая не лежит внутри области определения функции, т.е. не критическая точка.
не существует при х = 0, которая не лежит внутри области определения функции, т.е. не критическая точка.
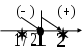
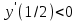 ,
, 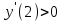
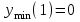
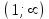 - область возрастания функции;
- область возрастания функции;
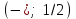 - область убывания функции.
- область убывания функции.
6)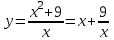 . Обл. опр.: х ≠ 0, (-; 0)U(0; );
. Обл. опр.: х ≠ 0, (-; 0)U(0; ); 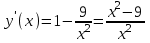
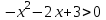 ,
, 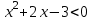
x = -3; 1
Область возрастания: (-3; 1), или [-3; 1] ▲
Экстремум функции
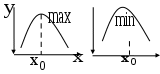
Точка х0 называется точкой максимума (минимума) функции f(x), если для всех х из некоторой окрестности этой точки выполняются неравенства
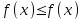 , то х0 – точка максимума;
, то х0 – точка максимума;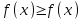 , то х0 – точка минимума.
, то х0 – точка минимума.Точки максимума и минимума называются точками экстремума, а значения функции в этих точках называются экстремумами функции.
Необходимые условия экстремума
Если функция y = f(x) имеет экстремум в точке х0, лежащий внутри области определения функции, то ее производная
 либо равна нулю, либо не существует.
либо равна нулю, либо не существует.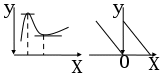
Производная функции
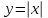 в точке х = 0 не существует, но экстремум в этой точке есть.
в точке х = 0 не существует, но экстремум в этой точке есть.Точки, в которых выполнены необходимые условия экстремума, называются критическими точками.
Замечание. Если в какой-то точке имеется экстремум, то эта точка критическая; обратно неверно, т.е. критическая точка не обязательно является точкой экстремума. Критическая точка должна входить в область определения функции.
Например, рассмотрим функцию y = x3.
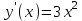 ,
, 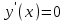 x= 0 – критическая точка, но экстремума нет.
x= 0 – критическая точка, но экстремума нет.Упр. Найти критические точки.
1)
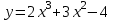 . Обл. опр.: (-; ).
. Обл. опр.: (-; ).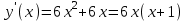 ,
, 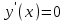 ,
, 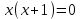
x = 0; -1 – критические точки.
2)
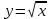 . Обл. опр.: 0; )
. Обл. опр.: 0; )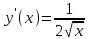 ,
,  не существует при х = 0, но эта точка не лежит внутри области определения, следовательно, не есть критическая точка.
не существует при х = 0, но эта точка не лежит внутри области определения, следовательно, не есть критическая точка.Вывод: Экстремума нет, поскольку не критических точек.
3)
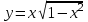 . Обл. опр.: -1; 1
. Обл. опр.: -1; 1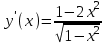 ,
,  при
при 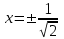 - критические точки, т.к. лежат внутри области определения функции.
- критические точки, т.к. лежат внутри области определения функции. не существует при х = 1, но не критические точки, поскольку не лежат внутри области определения функции.
не существует при х = 1, но не критические точки, поскольку не лежат внутри области определения функции.4)
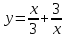 . Обл. опр.: (-; 0)U(0; )
. Обл. опр.: (-; 0)U(0; )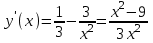 ,
, при
при 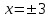 - критические точки, т.к. лежат внутри области определения функции.
- критические точки, т.к. лежат внутри области определения функции. не существует при х = 0, но не критические точки, поскольку не лежит внутри области определения функции.
не существует при х = 0, но не критические точки, поскольку не лежит внутри области определения функции.5)
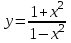 . Обл. опр.: (-; -1)U(-1; 1) U(1; )
. Обл. опр.: (-; -1)U(-1; 1) U(1; )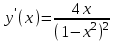 ,
,  при
при 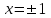 - критическая точки.
- критическая точки. не существует при х = 0, но не критические точки, поскольку не лежит внутри области определения функции.
не существует при х = 0, но не критические точки, поскольку не лежит внутри области определения функции.6)
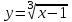 . Обл. опр.: (-; )
. Обл. опр.: (-; )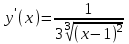 ,
,  не существует при х = 1- критическая точка.
не существует при х = 1- критическая точка.Достаточное условие экстремума

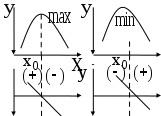
Если при переходе через критическую точку производная функции меняет знак с плюса на минус, то имеет место максимум функции, а если с минуса на плюс – минимум. Если же знак производной не меняется, то экстремума нет.
Замечание. Факт возрастания функции будем обозначать стрелкой вверх
 , а убывание – стрелкой вниз
, а убывание – стрелкой вниз 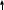 , тогда
, тогда
Схема исследования функции на экстремум и
области возрастания и убывания функции
1) Найти производную
 .
.2) Найти критические точки, которые лежат внутри области определения функции.
3) Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремума функции и области возрастания и убывания функции.
4) Найти экстремум функции.
Замечание. Критические точки отделяют область возрастания и область убывания функции.
Упр. Найти экстремумы и области возрастания и убывания функции.
1)
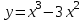 . Обл. опр.: (-; );
. Обл. опр.: (-; ); 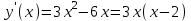 ;
;  х = 0; 2- критические точки. Наносим все критические точки на числовой прямой. Критические точки разбивают числовую ось на три области.
х = 0; 2- критические точки. Наносим все критические точки на числовой прямой. Критические точки разбивают числовую ось на три области.      II III II  |
Для определения знака
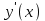 в каждой области используются следующие способы.
в каждой области используются следующие способы.а) Прямой способ. Возьмем контрольные точки в окрестности каждой критической точки и определим знак производной в контрольной точке.
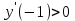 ,
, 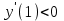 ,
, 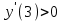
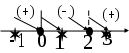
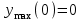 ,
, 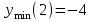
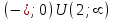 - область возрастания функции;
- область возрастания функции;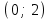 - область убывания функции.
- область убывания функции.б) Нанесем график
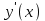

Корни: х = 0; 2

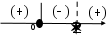
в) Метод интервалов.
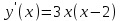 - стандартный вид
- стандартный видКорни: х = 0; 2
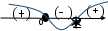
2)
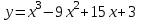 . Обл. опр.: (-; );
. Обл. опр.: (-; ); 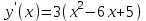 ;
;  х = 1; 5- критические точки.
х = 1; 5- критические точки.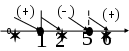
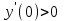 ,
, 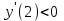 ,
, 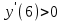
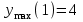 ,
, 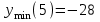
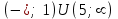 - область возрастания функции;
- область возрастания функции;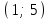
- область убывания функции.
3)
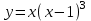 . Обл. опр.: (-; );
. Обл. опр.: (-; ); 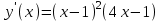 ;
;  х = 1; 1/4- критические точки.
х = 1; 1/4- критические точки.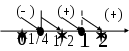
 ,
,  ,
, 
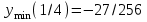
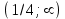 - область возрастания функции;
- область возрастания функции;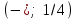 - область убывания функции.
- область убывания функции.4)
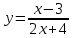 . Обл. опр.: (-;-2)U(-2; );
. Обл. опр.: (-;-2)U(-2; ); 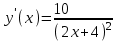 ;
;  не существует при х = -2, которая не лежит внутри области определения функции, т.е. не критическая точка, следовательно, экстремума нет.
не существует при х = -2, которая не лежит внутри области определения функции, т.е. не критическая точка, следовательно, экстремума нет.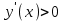 при всех х -2, следовательно,
при всех х -2, следовательно, 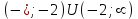 - область возрастания функции.
- область возрастания функции.5)
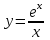 . Обл. опр.: (-; 0)U(0; );
. Обл. опр.: (-; 0)U(0; ); 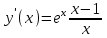 ;
;  х = 1- критическая точка.
х = 1- критическая точка. не существует при х = 0, которая не лежит внутри области определения функции, т.е. не критическая точка.
не существует при х = 0, которая не лежит внутри области определения функции, т.е. не критическая точка.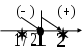
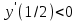 ,
, 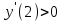
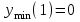
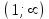 - область возрастания функции;
- область возрастания функции;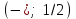 - область убывания функции.
- область убывания функции.6)
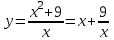 . Обл. опр.: х ≠ 0, (-; 0)U(0; );
. Обл. опр.: х ≠ 0, (-; 0)U(0; );