, х² – 9 =0, х =±3- критические точки.

не существует при х = 0, которая не лежит внутри области определения функции, т.е. не критическая точка.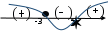



,

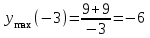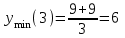
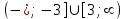- область возрастания функции;

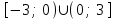- область убывания функции.
Наибольшее и наименьшее значение функции на отрезке

Наибольшим (наименьшим) значением функции на отрезке a;b называется такое значение, которое больше (меньше) всех других значений, принимаемых функцией на данном отрезке.

Теорема. Если функция f(x) непрерывна на отрезке a;b, то она принимает на этом отрезке наибольшее и наименьшее значения. Эти значения достигаются ею или в точках экстремума, лежащие внутри отрезка, или на концах отрезка.

Для отыскания наибольшего и наименьшего значения функции на отрезке, нужно:

• найти критические точки, лежащие внутри отрезка;

• подсчитать значения функции в критических точках и на концах отрезка;

• выбрать из найденных значений наибольшее и наименьшее.

Упр.

1) Найти наибольшее и наименьшее значение функции на отрезке

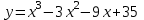, 0;4.

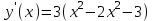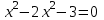▼ , , , х =-1; 3

х = -10;4, х = 30;4.

х	0	3	4
y(x)	35	8	15

2Наименьшее значение

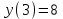
Наибольшее значение ▲

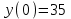2) Укажите наибольшее целое решение неравенства

---

, если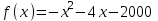



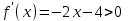▼ , х < -2. Отв. х = -3▲
Исследование функции без помощи производной

1)Найдите абсциссу точки максимума функции  

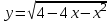
▼ Квадратный трехчлен 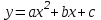 с отрицательным старшим коэффициентом достигает максимума в точке  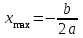, в нашем случае — в точке −2. Поскольку функция  возрастающая, а заданная функция определена при найденном значении переменной, она достигает максимума в той же точке, в которой достигает максимума подкоренное выражение.

 Ответ: −2 ▲

2) Найдите точку минимума функции  

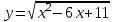
 ▼ Квадратный трехчлен 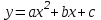  с положительным старшим коэффициентом достигает минимума в точке  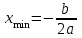, в нашем случае — в точке 3. Поскольку функция  возрастающая, а заданная функция определена при найденном значении переменной, она достигает минимума в той же точке, в которой достигает минимума подкоренное выражение.

 Ответ: 3 ▲

3) Найдите точку максимума функции . 

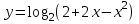▼ Квадратный трехчлен 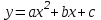  с отрицательным старшим коэффициентом достигает максимума в точке  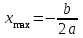, в нашем случае — в точке 1. Поскольку функция  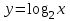возрастает, и функция  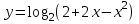определена в точке 1, она также достигает в ней максимума.

 Ответ: 1.

4) Найдите точку максимума функции  

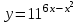
▼ Поскольку функция

---

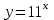
возрастающая, заданная функция достигает максимума в той же точке, в которой достигает максимума выражение 6х – х². Квадратный трехчлен  с отрицательным старшим коэффициентом достигает максимума в точке  , в нашем случае — в точке 3.

 Ответ: 3 ▲

---

Смотрите также файлы

• Трансформация человека в цифровую эпоху.docx

• Опишите структуру правоотношения. Охарактеризуйте основные элементы, входящие в его состав.docx

• Лабораторная работа 1 Документоориентированная субд по дисциплине Современные субд Студент гр з421П25.docx

• Реферат Контроль и самоконтроль в занятиях физической культурой и спортом. Профилактика травматизма.rtf

• Юридические коллизии содержание введние.docx