На данном этапе выполняется проверка соответствия модели оригиналу, т.е. используя известные статистические критерии, дается оценка адекватности модели, значимости коэффициентов модели, воспроизводимости опытов.

На 4-ом этапе используют полученную модель в работе реального объекта для наблюдения или управления этим объектом, дается численная оценка этого использования.

2.1. Обследования объекта моделирования

Математические модели, особенно использующие численные методы, требуют для своего построения значительных интеллектуальных, финансовых и временных затрат. Поэтому решение о разработке новой модели принимается лишь в случае отсутствия иных, более простых путей решения возникших проблем (например, модификации одной из существующих моделей). Необходимость в новой модели может появиться в связи с проведением научных исследований, выполнением проектно-конструкторских работ, созданием систем автоматического управления.

Основной целью обследования объекта моделирования является подготовка содержательной постановки задачи моделирования, т.е. списка основных вопросов об объекте моделирования, интересующих заказчика.

На этом этапе важную роль играют специалисты – постановщики задач, которые  должны не только хорошо разбираться в предметной области моделирования, знать возможности современной вычислительной техники, но и быть достаточно коммуникабельными, способными «разговорить» практиков, хорошо знающих объект моделирования.

На основании анализа всей собранной информации постановщик задачи должен сформулировать такие требования к будущей модели, которые: с одной стороны, удовлетворяли бы заказчика, а с другой - позволяли бы реализовать модель в заданные сроки и в рамках выделенных материальных средств.

Этап обследования объекта моделирования включает следующие работы:

• 
  выявление основных факторов, механизмов, влияющих на поведение объекта моделирования, определение параметров, позволяющих описывать моделируемый объект;
  
• 
  сбор и проверка имеющихся экспериментальных данных об объектах-аналогах, проведение при необходимости дополнительных экспериментов;
  
• 
  аналитический обзор литературных источников, анализ и сравнение между собой построенных ранее моделей данного объекта (или подобных рассматриваемому объекту);
  
• 
  анализ и обобщение всего накопленного материала, разработка общего плана создания математической модели.
  

---

На основе собранной информации постановщик и заказчик формулируют содержательную или техническую постановку задачи моделирования, которая, как правило, не бывает окончательной и может уточняться в процессе разработки модели.

Весь собранный материал об объекте, содержательная постановка задачи, требования к реализации модели и представлению результатов, оформляются в виде технического задания на проектирование и разработку модели.

Ниже приведен пример содержательной постановки задачи о баскетболисте.

Пример. Содержательная постановка задачи о баскетболисте: Необходимо разработать математическую модель, позволяющую описать полет баскетбольного мяча, брошенного игроком в баскетбольную корзину.

Модель должна позволять:

• 
  вычислять положение мяча в любой момент времени;
  
• 
  определять точность попадания мяча в корзину после броска при различных начальных параметрах.
  

Исходные данные:

• 
  масса и радиус мяча;
  
• 
  начальные координаты, начальная скорость и угол броска мяча;
  
• 
  координаты центра и радиус корзины.
  

 

2.2 Концептуальная постановка задачи моделирования

Содержательная модель является синтезом когнитивных моделей, каждого из членов рабочей группы. На основании содержательной модели разрабатывается концептуальная, или «естественнонаучная» постановка задачи моделирования.

Концептуальная постановка задачи моделирования - это сформулированный в терминах конкретных дисциплин (физики, химии, биологии и т.д.) перечень основных вопросов, интересующих заказчика, а также совокупность гипотез относительно свойств и поведения объекта моделирования.

Наибольшие трудности при формулировке концептуальной постановки приходится преодолевать в моделях, находящихся на «стыке» различных дисциплин. Различия традиций, понятий и языков, используемых для описания одних и тех же объектов, являются очень серьезными препятствиями, возникающими при создании «междисциплинарных» моделей.

Например, такие понятия как «прибыль» и «баланс» вызывают совершенно разные ассоциации у экономиста и математика. Можно сказать, что когнитивные модели, стоящие за этими понятиями, у этих двух специалистов совершенно различны. Если экономист, говоря о прибыли и балансе, связывает с этими понятиями конкретное производство, цену и себестоимость продукции, то для математика данные понятия выглядят более формально – как результаты решения некоторых математических уравнений. При этом практически невозможно научить математика мыслить как экономиста, а экономиста - как математика. И тот, и другой способ восприятия имеет свои достоинства и недостатки. Экономист никогда не сделает ошибок, которые может допустить математик, без должных знаний в предметной области. В то же время, используя формальные преобразования математических соотношений, математик может получить решения, недоступные экономисту.

---

Пример. Концептуальная постановка задачи о баскетболисте. Движение баскетбольного мяча может быть описано в соответствии с законами классической механики Ньютона.

Примем следующие гипотезы:

• 
  объектом моделирования является баскетбольный мяч радиуса R;
  
• 
  мяч будем считать материальной точкой массой m, положение которой совпадает с центром масс мяча;
  
• 
  движение происходит в поле сил тяжести с постоянным ускорением свободного падения g и описывается уравнениями классической механики Ньютона;
  
• 
  движение мяча происходит в одной плоскости, перпендикулярной поверхности Земли и проходящей через точку броска и центр корзины;
  
• 
  пренебрегаем сопротивлением воздуха и возмущениями, вызванными собственным вращением мяча вокруг центра масс.
  

Рассмотрим особенности приведенной в примере концептуальной постановки задачи о баскетболисте. Первая из перечисленных гипотез особенно важна, так как она выделяет объект моделирования. В данном случае объект можно считать простым. Однако в качестве объекта моделирования можно рассматривать систему «игрок - мяч - кольцо». Требуемая для описания подобной системы модель будет уже намного сложнее, так как игрок в свою очередь представляет собой сложную биомеханическую систему и его моделирование является далеко не тривиальной задачей. В данной ситуации выбор в качестве объекта моделирования только мяча обоснован, поскольку именно его движение требуется исследовать, а влияние игрока можно учесть через начальные параметры броска. Для сложных систем выбор объекта моделирования - далеко не простая и неоднозначная задача.

Гипотеза о том, что мяч можно считать материальной точкой, широко применяется для исследования движений тел в механике. В рассматриваемом случае она оправдана в силу симметрии формы мяча и малости его радиуса по сравнению с характерными расстояниями перемещения мяча.

Гипотезу о применимости в данном случае законов классической механики можно обосновать огромным экспериментальным материалом, связанным с изучением движения тел вблизи поверхности Земли со скоростями много меньше скорости света. Предположение о постоянстве ускорения свободного падения также представляется обоснованным. А вот если бы моделировалось движение баллистической ракеты, то пришлось бы учитывать изменение ускорения свободного падения в зависимости от высоты и широты места.

Гипотеза о движении мяча в плоскости, перпендикулярной поверхности Земли, ограничивает класс рассматриваемых траекторий и значительно упрощает модель. Траектория мяча может не лежать в одной плоскости, если при броске он сильно подкручивается вокруг вертикальной оси. В этом случае поток воздуха, обтекающий мяч, становится не симметричным. Так как поток неразрывный, а элементарные струйки № 1,2 и 3 должны пройти бОльший путь, чем струйка №4, следовательно, и скорости этих струек должны быть выше. В соответствии с законом Бернулли, давление газа на поверхность меньше там, где скорость потока выше. Поэтому на мяч будет действовать дополнительная сила, направленная в сторону. Этот эффект будет проявляться тем больше, чем больше скорость центра масс мяча и скорость его вращения. Для баскетбола характерны относительно низкие скорости полета мяча (порядка 10 м/с). При этом довольно редко используется подкрутка мяча рукой. Поэтому гипотеза о движении мяча в одной плоскости кажется оправданной. Ее использование позволяет отказаться от построения значительно более сложной трехмерной модели движения мяча.

---

Гипотеза об отсутствии влияния сопротивления воздуха наименее обоснована. При движении тела в газе или жидкости сила сопротивления увеличивается с ростом скорости движения. Учитывая невысокие скорости движения мяча, его правильную обтекаемую форму и малые дальности бросков, указанная гипотеза может быть принята в качестве первого приближения.

Следует отметить, что концептуальная постановка задачи моделирования в отличие от содержательной постановки использует терминологию конкретной дисциплины (в рассматриваемом случае - механики). При этом моделируемый реальный объект (мяч) заменяется его механической моделью (материальной точкой). Фактически в приведенном примере концептуальная постановка свелась к постановке классической задачи механики о движении материальной точки в поле сил тяжести. Концептуальная постановка более абстрактна по отношению к содержательной, так как материальной точке можно сопоставить произвольный материальный объект, брошенный под углом к горизонту: футбольный мяч, ядро, камень или артиллерийский снаряд.

2.3. Математическая постановка задачи моделирования

Концептуальная постановка позволяет сформулировать математическую постановку задачи моделирования, т.е. совокупность математических соотношений, описывающих поведение и свойства объекта моделирования.

Как было отмечено ранее, совокупность математических соотношений определяет вид оператора модели. Наиболее простым будет оператор модели в случае, если он представлен системой алгебраических уравнений.

Следует отметить, что во многих областях знаний (механике, физике, биологии и т.д.) принято выделять законы, справедливые для всех объектов исследования данной области знаний, и соотношения, описывающие поведение отдельных объектов или их совокупностей. К числу первых в физике и механике относятся, например, уравнения баланса массы, количества движения, энергии и т.д., справедливые при определенных условиях для любых материальных тел, независимо от их конкретного строения, структуры, состояния, химического состава. Уравнения этого класса подтверждены огромным количеством экспериментов, хорошо изучены и в силу этого применяются в соответствующих математических моделях как данность. Соотношения второго класса в физике и механике называют уравнениями состояния. Они устанавливают особенности поведения материальных объектов или их совокупностей (например, жидкостей или газов) при воздействиях различных внешних факторов.

---

В качестве классических примеров определяющих соотношений можно привести закон Гука в теории упругости или уравнение Клапейрона для идеальных газов.

Соотношения этого класса гораздо менее изучены, а в ряде случаев их приходится устанавливать самому исследователю. Необходимо отметить, что определяющие соотношения - это основной элемент, «сердцевина» любой математической модели физико-механических процессов. Именно ошибки в выборе или установлении определяющих соотношений приводят к количественно неверным результатам моделирования.

3. Принципы построения математических моделей

Математическое моделирование многие считают скорее искусством, чем стройной и законченной теорией. Здесь очень велика роль опыта, интуиции и других интеллектуальных качеств человека. Поэтому невозможно написать достаточно формализованную инструкцию, определяющую, как должна строиться модель той или иной системы. Тем не менее отсутствие точных правил не мешает опытным специалистам строить удачные модели. К настоящему времени уже накоплен значительный опыт, дающий основание сформулировать некоторые принципы и подходы к построению моделей. При рассмотрении порознь каждый из них может показаться довольно очевидным. Но совокупность взятых вместе принципов и подходов далеко не тривиальна. Многие ошибки и неудачи в практике моделирования являются прямым следствием нарушения этой методологии. Принципы определяют те общие требования, которым должна удовлетворять правильно построенная модель. Рассмотрим эти принципы. 1 .Адекватность. Этот принцип предусматривает соответствие модели целям исследования по уровню сложности и организации, а также соответствие реальной системе относительно выбранного множества свойств. До тех пор, пока не решен вопрос, правильно ли отображает модель исследуемую систему, ценность модели незначительна. 2. Соответствие модели решаемой задаче. Модель должна строиться для решения определенного класса задач или конкретной задачи исследования системы. Попытки создания универсальной модели, нацеленной на решение большого числа разнообразных задач, приводят к такому усложнению, что она оказывается практически непригодной. Опыт показывает, что при решении каждой конкретной задачи нужно иметь свою модель, отражающую те аспекты системы, которые являются наиболее важными в данной задаче. Этот принцип связан с принципом адекватности. 3. Упрощение при сохранении существенных свойств системы. Модель должна быть в некоторых отношениях проще прототипа - в этом смысл моделирования. Чем сложнее рассматриваемая система, тем по возможности более упрощенным должно быть ее описание, умышленно утрирующее типичные и игнорирующее менее существенные свойства. Этот принцип может быть назван принципом абстрагирования от второстепенных деталей. 4. Соответствие между требуемой точностью результатов моделирования и сложностью модели. Модели по своей природе всегда носят приближенный характер. Возникает вопрос, каким должно быть это приближение. С одной стороны, чтобы отразить все сколько-нибудь существенные свойства, модель необходимо детализировать. С другой стороны, строить модель, приближающуюся по сложности к реальной системе, очевидно, не имеет смысла. Она не должна быть настолько сложной, чтобы нахождение решения оказалось слишком затруднительным. Компромисс между этими двумя требованиями достигается нередко путем проб и ошибок. Практическими рекомендациями по уменьшению сложности моделей являются: • изменение числа переменных, достигаемое либо исключением несущественных переменных, либо их объединением. Процесс преобразования модели в модель с меньшим числом переменных и ограничений называют агрегированием. Например, все типы ЭВМ в модели гетерогенных сетей можно объединить в четыре типа - ПЭВМ (или обычные компьютеры), рабочие станции, большие ЭВМ (мейнфреймы), кластерные ЭВМ; • изменение природы переменных параметров. Переменные параметры рассматриваются в качестве постоянных, дискретные - в качестве непрерывных и т.д. Так, условия распространения радиоволн в модели радиоканала для простоты можно принять постоянными; • изменение функциональной зависимости между переменными. Нелинейная зависимость заменяется обычно линейной, дискретная функция распределения вероятностей - непрерывной; • изменение ограничений (добавление, исключение или модификация). При снятии ограничений получается оптимистичное решение, при введении - пессимистичное. Варьируя ограничениями, можно найти возможные граничные значения эффективности. Такой прием часто используется для нахождения предварительных оценок эффективности решений на этапе постановки задач; • ограничение точности модели. Точность результатов модели не может быть выше точности исходных данных. 5. Баланс погрешностей различных видов. В соответствии с принципом баланса необходимо добиваться, например, баланса систематической погрешности моделирования за счет отклонения модели от оригинала и погрешности исходных данных, точности отдельных элементов модели, систематической погрешности моделирования и случайной погрешности при интерпретации и осреднении результатов. 6. Многовариантность реализаций элементов модели. Разнообразие реализаций одного и того же элемента, отличающихся по точности (а следовательно, и по сложности), обеспечивает регулирование соотношения «точность/сложность». 7. Блочное строение. При соблюдении принципа блочного строения облегчается разработка сложных моделей и появляется возможность использования накопленного опыта и готовых блоков с минимальными связями между ними. Выделение блоков производится с учетом разделения модели по этапам и режимам функционирования системы. К примеру, при построении модели для системы радиообнаружения можно выделить модель работы излучателей, модель обнаружения излучателей, модель пеленгования и т.д. В зависимости от конкретной ситуации возможны следующие подходы к построению моделей: • непосредственный анализ функционирования системы; • проведение ограниченного эксперимента на самой системе; • использование аналога, • анализ исходных данных. Имеется целый ряд систем, которые допускают проведение непосредственных исследований по выявлению существенных параметров и отношений между ними. Затем либо применяются известные математические модели, либо они модифицируются, либо предлагается новая модель. Таким образом, например, можно вести разработку модели для направления связи в различных временных условиях и ситуациях. При проведении эксперимента выявляются значительная часть существенных параметров и их влияние на эффективность системы. Такую цель преследуют, например, все командно-штабные игры и большинство учений, о которых сообщают СМИ. Если метод построения модели системы не ясен, но ее структура очевидна, то можно воспользоваться сходством с более простой системой, модель для которой существует. К построению модели можно приступить на основе анализа исходных данных, которые уже известны или могут быть получены. Анализ позволяет сформулировать гипотезу о структуре системы, которая затем апробируется. Так появляются первые модели нового образца иностранной техники при наличии предварительных данных об их технических параметрах. Разработчики моделей находятся под действием двух взаимно противоречивых тенденций: стремления к полноте описания и стремления к получению требуемых результатов возможно более простыми средствами. Достижение компромисса ведется обычно по пути построения серии моделей, начинающихся с предельно простых и восходящих до высокой сложности (существует известное правило: начинай с простых моделей, а далее усложняй). Простые модели помогают глубже понять исследуемую проблему. Усложненные модели используются для анализа влияния различных факторов на результаты моделирования. Такой анализ позволяет исключать некоторые факторы из рассмотрения. Сложные системы требуют разработки целой иерархии моделей, различающихся уровнем отображаемых операций. Выделяют такие уровни, как вся система, подсистемы, управляющие объекты и др. Рассмотрим один конкретный пример - модель развития экономики (модель Харрода). Эта упрощенная модель развития экономики страны предложена английским экономистом Р. Харродом. В модели учитывается один определяемый фактор - капитальные вложения, а состояние экономики оценивается через размер национального дохода. Для математической постановки задачи введем следующие обозначения: • Yt - национальный доход в год t; • Kt - производственные фонды в год t; • Ct — объем потребления в год t; • St - объем накопления в год t; • Vt - капитальные вложения в год t. Будем предполагать, что функционирование экономики происходит при выполнении следующих условий: • условие баланса доходов и расходов за каждый год • условие исключения пролеживания капитала • условие пропорционального деления национального годового дохода Два условия принимаются для характеристики внутренних экономических процессов. Первое условие характеризует связь капитальных вложений и общей суммы производственных фондов, второе - связь национального годового дохода и производственных фондов. Капитальные вложения в год t могут рассматриваться как прирост производственных фондов, или производная от функции «производственные фонды» принимается как капитальные годовые вложения: Национальный доход в каждый год принимается как отдача производственных фондов с соответствующим нормативным коэффициентом фондоотдачи: Соединяя условия задачи, можно получить следующее соотношение: 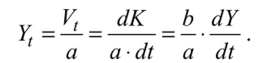Отсюда следует итоговое уравнение Харрода: 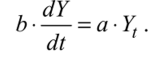Его решением является экспоненциальное изменение национального дохода по годовым интервалам: Несмотря на упрощенный вид математической модели, ее результат может быть использован для укрупненного анализа национальной экономики. Параметры а и b могут стать параметрами управления при выборе плановой стратегии развития в целях максимального приближения к предпочтительной траектории изменения национального дохода или для выбора минимального интервала времени достижения заданного уровня национального дохода.

---

Смотрите также файлы

• .docx

• Содержание введение краткое описание проделанной работы в период прохождения производственной практики заключение введение.docx

• Практических заданий по дисциплине бухгалтерский финансовый учет и отчетность.docx

• .docx

• Краевое государственное бюджетное профессиональное образовательное учреждение красноярский колледж отраслевых технологий и предпринимательства.docx