4. Форма представления математических моделей

В общем смысле формы преставления математической модели определяют:

• 
  инвариантная форма – это запись соотношений в математической модели в общем виде с помощью традиционного математического языка без относительно (не учитывая) к методу решения.
  
• 
  алгоритмическая форма учитывает структуру модели, соотношение и взаимосвязи между величинами, а также рассматривается относительно принятого метода численного решения – в виде алгоритма.
  
• 
  аналитическая форма представляет собой явные выражения, взаимосвязи выходных параметров, как функций входных, внутренних, внешних параметров. Она получается в виде результата аналитического решения исходных уравнений модели или обработки статистических данных по принятым методам идентификации.
  
• 
  схемная или графическая форма – это представление модели на некотором графическом языке в виде графов, например, модель сетевого планирования выполнения работ, диаграмм, чертежей, схем и т.д. Дальнейшее использование такой формы представления модели возможно при наличии обобщённых правил истолкования отдельных элементов этой формы и их перевода на языки математических описаний или другие формы.
  

Среди алгоритмических форм наибольшее распространение получили имитационные модели, суть которых состоит в том, что модель имитирует физические или информационные процессы объекта при задании различных входных воздействий в некоторой среде, которая имитирует реальную среду работы объекта.


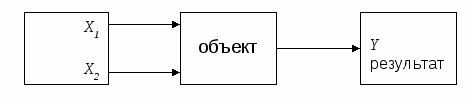
5. Методы получения моделей

Получение моделей объектов, т.е. переход к их математическому описанию, является не форматированной процедурой, и в каждом конкретном случае, решение принимается индивидуально. Другими словами, все решения по моделированию, по оценке входных и выходных параметров, по исследованию математических зависимостей, по оценке взаимосвязей между параметрами, принимает разработчик модели. Когда эти вопросы решены, т.е. получена конкретная модель в виде математического выражения, все другие действия или операции, такие как: расчёт численных значений параметров модели, определение областей адекватности, значимости и т.д. – алгоритмизированы, т.е. формализованы и могут выполнятся по определённым правилам на ЭВМ.

---

В общем смысле методы получения моделей разделяют на теоретические и экспериментальные.

Теоретические методы основаны на изучении физических закономерностей данного объекта или процесса, а также в определении соответствующих этим закономерностям математических описаний или обоснований. Теоретические методы получения модели приводят в результате к моделям в виде алгебраических, дифференциальных, трансцендентных уравнений.

При необходимости здесь возможны некоторые упрощения и допущения известных физических уравнений и закономерностей (например, уравнение теплопроводности, связывающее большое количество параметров, можно представить в виде зависимости от 2-х, 3-х параметров). Экспериментальные методы основаны на исследовании внешних проявлений свойств объекта, фиксируемых во время эксплуатации этих объектов или при проведении целенаправленных активных экспериментов. По форме связи между входными и выходными величинами эти методы могут быть детерминированными или стохастическими. Первые – это такие, когда каждому конкретному значению входной величины объекта соответствует конкретное значение выходной величины, т.е. величины связаны функционально. Если же такая связь нарушается, т.е. на объект действует случайным образом возмущение и значения выходных величин не всегда соответствуют значениям входных, т.е. в составе выходного значения величины присутствует доля случайности, то такие процессы называют стохастическими. Здесь степень взаимосвязи оценивается коэффициентом корреляции, численное значение которого находится в интервале 0..1.

Заключение
Объекты и операции более общих математических моделей часто ассоциируются с множествами действительных чисел, которые могут быть соотнесены с результатами физических измерений.

Математическое моделирование - метод качественного и (или) количественного описания процесса с помощью, так называемой математической модели, при построении которой реальный процесс или явление описывается с помощью того или иного адекватного математического аппарата. Математическое моделирование является неотъемлемой частью современного исследования.

Список литературы

1. 
   Башмаков М. И. Алгебра и начала анализа 10-11. М.: Просвещение, 1992.
   
2. 
   Виленкин Н. Л. Функции в природе и технике. – М.: Просвещение, 1978
   
3. 
   Гейн А. Г. Земля Информатика. – Екатеринбург: Издательство Уральского университета, 1997
   
4. 
   Гнеденко Б. В. Введение в специальность математика. – М: Наука, 1991
   
5. 
   Гнеденко Б. В. Математика в современном мире. М: Просвещение, 1980.
   
6. 
   Костюкова Н.И. Основные принципы математического моделирования. – 2011. - №5. – С.44-48.
   
7. 
   Перельман Я. И. Занимательная алгебра. М: АО “Столетие”, 1994
   
8. 
   Хургин Я. И. Ну и что? (Разговоры математика с биологами и радистами, врачами и технологами… о математике и ее связях с другими науками). М.: Молодая гвардия, 1967.
   
9. 
   Шибасов Л. П., Шибасова З. Ф. За страницами учебника математики. – М.: Просвещение, 1997
   

---

---

Смотрите также файлы

• .docx

• Содержание введение краткое описание проделанной работы в период прохождения производственной практики заключение введение.docx

• Практических заданий по дисциплине бухгалтерский финансовый учет и отчетность.docx

• .docx

• Краевое государственное бюджетное профессиональное образовательное учреждение красноярский колледж отраслевых технологий и предпринимательства.docx