ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 27
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ПРИ ДОКАЗАТЕЛЬСТВЕ ТОЖДЕСТВ И НЕРАВЕНСТВ
Решение многих задач математики опирается на доказательство тождеств и неравенств. Для их доказательства существуют различные способы. Изучая в школе и в вузе тему «Производная и ее применение», мы рассматриваем такие вопросы, как монотонность функции, знакопостоянство функции, экстремумы функций. Здесь мы хотим расширить круг задач, которые можно решить, применяя производную, для чего используем теоремы из математического анализа. Тем более что методы их решения можно использовать и при решении задач из различных разделов математики.
Теорема 1. Пусть на отрезке
задана функция 
. Для того, чтобы эта функция была постоянной на этом отрезке, необходимо и достаточно, чтобы во всех точках отрезка существовала производная 
, и чтобы она всюду на отрезке была равна нулю [6].Используя эту теорему, можно доказать тождества вида
, на некотором промежутке 
. Для чего достаточно показать, что на этом промежутке 
(
– константа) и для некоторого 
из этого промежутка 
.Рассмотрим следующие примеры.
Пример 1. Доказать тождество
(1)Для доказательства этого тождества рассмотрим следующую функцию
Эта функция дифференцируема в промежутке
. Найдем 
и покажем, что 
в промежутке .
Значит, по теореме 1
( – константа).Для нахождения
вычислим значение функции 
в точке 
. Имеем
.Отсюда следует, что
.Значит
для всех
.Тождество (1) доказано.
Пример 2. Доказать тождество
(2)Рассмотрим функцию
.Находим
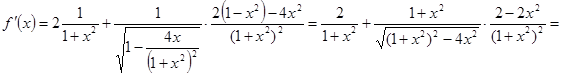
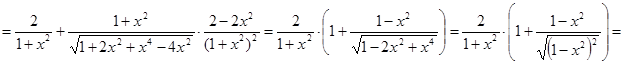
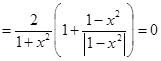, если 
.Отсюда следует, что
(
– константа) для . Для нахождения используем непрерывность функции на всей числовой оси и равенства
.Этим тождество (2) доказано.
Пример 3. Доказать тождество
(3)Рассмотрим функцию
Эта функция определена и дифференцируема для всех
.Находим
, если 
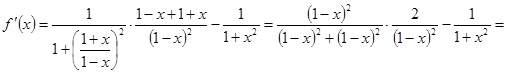
.Отсюда следует, что
( – константа). Для нахождения с, находим
.Этим тождество (3) доказано.
Такой способ доказательства тождеств носит некоторый самостоятельный характер, который можно использовать при доказательстве других тождеств.
Теорема 2. Пусть функция
определена и дифференцируема на отрезке 
. Если на этом отрезке выполняется условие 
, то на этом отрезке функция возрастающая (убывающая) и для любого х из отрезка справедливы соотношения:
(см. рис.1) [6].В этой теореме точек отрезка
, где 
, конечное число.
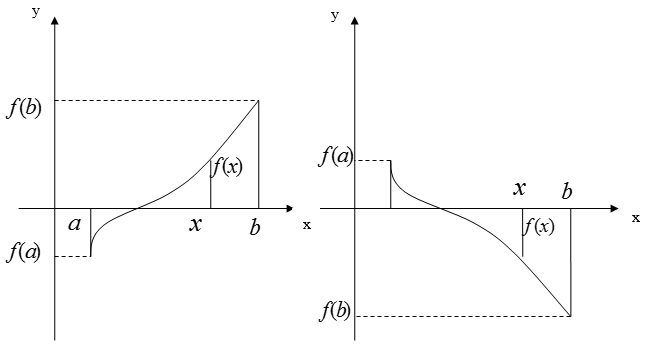
Рис. 1.
Используя эту теорему, докажем следующие функциональные неравенства. Рассмотрим примеры.
Пример 3. Справедливо неравенство
, 
(4)Рассмотрим функцию
Так как эта функция теряет смысл при
, то мы будем рассматривать 
в промежутке 
. Здесь дифференцируема и
.Но при
будет 
(это неравенство можно доказать, используя монотонность функции 
в данном промежутке). Значит, в промежутке 
, и 
убывает. Значит 
для или 
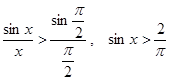. Отсюда, учитывая то, что при и 
в (4) выполняются равенства, имеем