ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 29
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Иначе говоря,
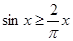 ,
, 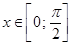 .
.
Это неравенство можно было доказать и графически.
Пример 4. Справедливо неравенство
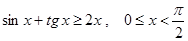 . (5)
. (5)
Рассмотрим функцию
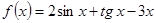 , для
, для 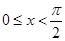 .
.
Она дифференцируема в указанном промежутке и её производная будет
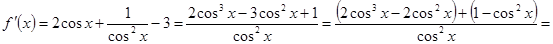
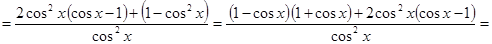
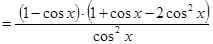 .
.
Здесь
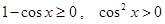
и
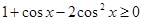 при
при 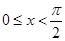 ;
;
(это следует из того, что квадратный трехчлен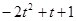 на отрезке
на отрезке 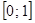 принимает неотрицательные значения).
принимает неотрицательные значения).
Поэтому , т.е.
, т.е. 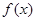 – возрастающая функция, значит
– возрастающая функция, значит
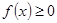 или
или 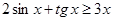 , при
, при 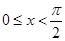 .
.
Отсюда, в частности, вытекает:
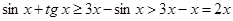
,
т. е.
 .
.
(Здесь мы использовали неравенство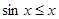 , для
, для 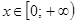 . Это неравенство также можно получить, используя монотонность функции
. Это неравенство также можно получить, используя монотонность функции 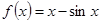 ).
).
Часто на школьных олимпиадах по математике встречаются задачи на сравнение двух чисел, заданных в виде степеней. Для решения этих задач можно использовать следующую теорему.
Теорема 3. Пусть для чисел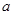 и
и 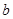 выполняется условие
выполняется условие 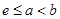 . Тогда справедливо следующее неравенство:
. Тогда справедливо следующее неравенство:
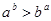 (6)
(6)
Доказательство. Рассмотрим функцию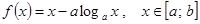 . Эта функция определена и дифференцируема на отрезке
. Эта функция определена и дифференцируема на отрезке  и
и
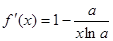 .
.
Так как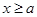 и
и 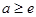 (тогда
(тогда 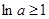 ), значит
), значит 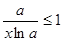 .
.
Таким образом
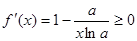 .
.
Отсюда, используя теорему 2, следует, что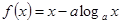
возрастающая на отрезке функция.
функция.
Используя свойство возрастающей функции на отрезке
на отрезке  , имеем
, имеем
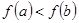 .
.
У нас
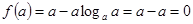 .
.
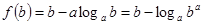 .
.
Отсюда
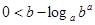 или
или 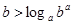 .
.
Потенцируя это неравенство, получим
 .
.
Что и требовалось доказать.
Значит, при условиях теоремы из двух степеней та степень больше, где показатель степени больше. Нетрудно заметить, что при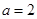 и
и 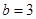 неравенство (6) не выполняется.
неравенство (6) не выполняется.
Хотелось бы отметить, что теорему 2 можно использовать при выполнения задания ЕГЭ части В на нахождение наибольшего и наименьшего значения функции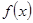 на отрезке
на отрезке  .
.
Прием использования производной для преобразования алгебраических и тригонометрических выражений основан на том, производная иногда имеет значительно более простой вид, чем исходная функция, благодаря чему, она легко интегрируется, что и позволяет найти искомое преобразование исходного выражения:
Задача 1 Упростить выражение: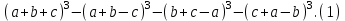
Решение: Обозначив данное выражение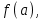 будем иметь:
будем иметь:
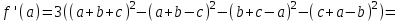
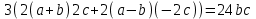
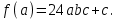
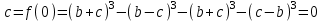
Таким образом, заданное выражение (1) равно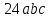 .
.
Задача 2. Упростить выражение:
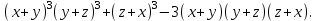
Решение: Обозначив это выражение через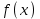 , будем иметь:
, будем иметь:
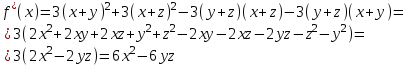
отсюда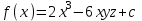 .
.
и при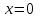 получаем:
получаем: 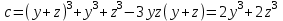
Так что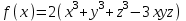
Задача 3. Упростить запись функции:
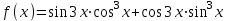 (2)
(2)
Решение: Применение обычного аппарата тригонометрии приведёт к относительно громоздким выкладкам. Здесь удобнее воспользоваться производной:
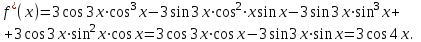
Отсюда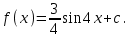
Найдём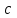 :
: 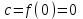
Таким образом функция (2) равна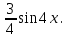
Задача 4. Упростить запись многочлена:
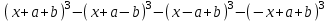 (3)
(3)
Решение: Обозначим многочлен (3) через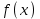 и найдём последовательно первую и вторую производные этой функции:
и найдём последовательно первую и вторую производные этой функции:
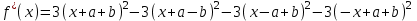
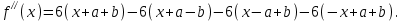
Ясно, что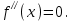
Поэтому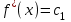 , где
, где 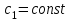 , найдём
, найдём 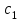 : при
: при 
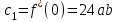 ,
, 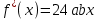 .
.
Задания для самостоятельного решения.
1. Проверить тождество:
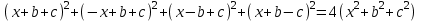
2.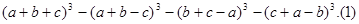
3. Проверить тождество:
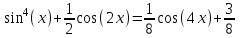
4.
5. Упростить запись многочлена:
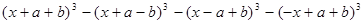
6.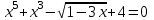
7.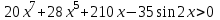
8. Выяснить, сколько действительных корней имеет уравнение:
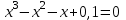
9.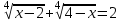
10. Проверьте, справедливо ли для всех действительных х следующее неравенство: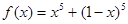
Список литературы
1.Агаханов С.А. Нахождение наименьшего и наибольшего значений функций на заданном
отрезке // Материалы ежегодной научно-практ. конф. – Махачкала: Институт (филиал) МГМУ, 2012.-С. 102-105.
2.В
Иначе говоря,
Это неравенство можно было доказать и графически.
Пример 4. Справедливо неравенство
Рассмотрим функцию
Она дифференцируема в указанном промежутке и её производная будет
Здесь
и
(это следует из того, что квадратный трехчлен
Поэтому
Отсюда, в частности, вытекает:
,
т. е.
(Здесь мы использовали неравенство
Часто на школьных олимпиадах по математике встречаются задачи на сравнение двух чисел, заданных в виде степеней. Для решения этих задач можно использовать следующую теорему.
Теорема 3. Пусть для чисел
Доказательство. Рассмотрим функцию
Так как
Таким образом
Отсюда, используя теорему 2, следует, что
возрастающая на отрезке
Используя свойство возрастающей функции
У нас
Отсюда
Потенцируя это неравенство, получим
Что и требовалось доказать.
Значит, при условиях теоремы из двух степеней та степень больше, где показатель степени больше. Нетрудно заметить, что при
Хотелось бы отметить, что теорему 2 можно использовать при выполнения задания ЕГЭ части В на нахождение наибольшего и наименьшего значения функции
Применение производной для упрощения алгебраических и тригонометрических выражений.
Прием использования производной для преобразования алгебраических и тригонометрических выражений основан на том, производная иногда имеет значительно более простой вид, чем исходная функция, благодаря чему, она легко интегрируется, что и позволяет найти искомое преобразование исходного выражения:
Задача 1 Упростить выражение:
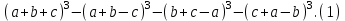
Решение: Обозначив данное выражение
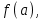 будем иметь:
будем иметь: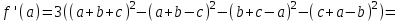
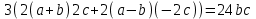
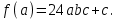
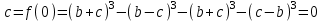
Таким образом, заданное выражение (1) равно
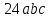 .
. Задача 2. Упростить выражение:
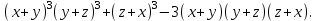
Решение: Обозначив это выражение через
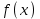 , будем иметь:
, будем иметь: 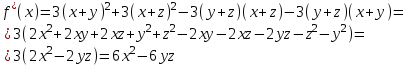
отсюда
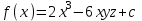 .
. и при
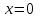 получаем:
получаем: 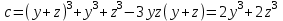
Так что
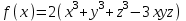
Задача 3. Упростить запись функции:
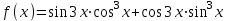 (2)
(2)Решение: Применение обычного аппарата тригонометрии приведёт к относительно громоздким выкладкам. Здесь удобнее воспользоваться производной:
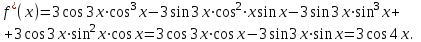
Отсюда
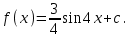
Найдём
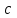 :
: 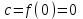
Таким образом функция (2) равна
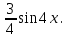
Задача 4. Упростить запись многочлена:
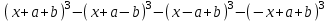 (3)
(3)Решение: Обозначим многочлен (3) через
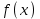 и найдём последовательно первую и вторую производные этой функции:
и найдём последовательно первую и вторую производные этой функции: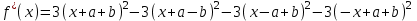
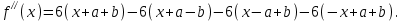
Ясно, что
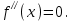
Поэтому
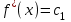 , где
, где 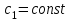 , найдём
, найдём 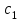 : при
: при 
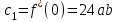 ,
, 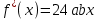 .
.Задания для самостоятельного решения.
1. Проверить тождество:
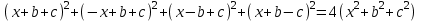
2.
3. Проверить тождество:
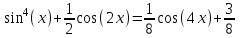
4.
5. Упростить запись многочлена:
6.
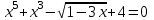
7.
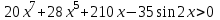
8. Выяснить, сколько действительных корней имеет уравнение:
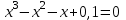
9.
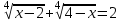
10. Проверьте, справедливо ли для всех действительных х следующее неравенство:
Список литературы
1.Агаханов С.А. Нахождение наименьшего и наибольшего значений функций на заданном
отрезке // Материалы ежегодной научно-практ. конф. – Махачкала: Институт (филиал) МГМУ, 2012.-С. 102-105.
2.В