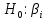Файл: Рис. 14. 1 Следует обратить внимание на то, что в отличие от е, первые три составляющие (компоненты) и,, v, с, являются закономерными, неслучайными..docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 52
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
влияние волн экономической активности Кондратьева, демографических «ям», циклов солнечной активности и т.п.):
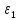, - случайная компонента, отражающая влияние не поддающихся учету и регистрации случайных факторов.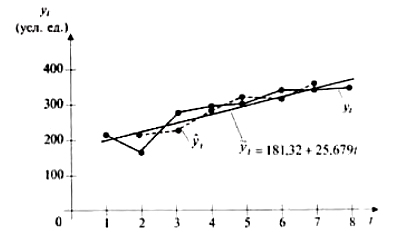
Рис. 14.1
Следует обратить внимание на то, что в отличие от е, первые три составляющие (компоненты) и,, v, с, являются закономерными, неслучайными.
Важнейшей классической задачей при исследовании экономических временных рядов является выявление и статистическая оценка основной тенденции развития изучаемого процесса и отклонений от нее. Отметим основные эта пы анализа временных рядов:
• графическое представление и описание поведения временного ряда;
• выделение и удаление закономерных (неслучайных) составляющих временного ряда (тренда, сезонных и циклических составляющих);
• сглаживание и фильтрация (удаление низко- или высокочастотных составляющих временного ряда);
• исследование случайной составляющей временного ряда, построение и проверка адекватности математической модели для се описания;
• прогнозирование развития изучаемого процесса на основе имеющегося временного ряда;
• исследование взаимосвязи между различными временными рядами.
Среди наиболее распространенных методов анализа временных рядов выделим корреляционный и спектральный анализ, модели авторегрессии и скользящей средней. О некоторых из них речь пойдет ниже
14.1. Общие сведения о временных рядах и задачах их анализа
Анализ временных рядов представляет собой самостоятельную, весьма обширную и одну из наиболее интенсивно развивавшихся областей математической статистики.
Под временным рядом (динамическим рядом, или рядом динамики) в экономике подразумевается последовательность наблюдений некоторого признака (случайной величины) Х в последовательные равноотстоящие моменты времени. Отдельные наблюдения называются уровнями ряда, которые будем обозначать
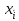(t = 1, 2, …,n), где n – число уровней.
В табл. 14.1 приведены данные, отражающие цену и спрос на некоторый товар за восьмилетний период (усл. ед.), т.е. два временных ряда - цены товара х, и спроса у, на него.
Таблица 14.1
| Год, t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Цена, 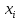 | 492 | 462 | 350 | 317 | 340 | 351 | 368 | 381 |
| Спрос, 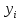 | 213 | 171 | 291 | 309 | 317 | 362 | 351 | 361 |
В качестве примера на рис. 14.1 временной ряд
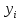, изображен графически.В общем виде при исследовании экономического временного ряда
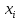, выделяются несколько составляющих:
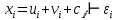, (t = 1, 2, …, n),где
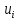, - тренд, плавно меняющаяся компонента, описывающая чистое влияние долговременных факторов, т.е. длительную («вековую») тенденцию изменения признака (например, рост населения, экономическое развитие, изменение структуры потребления и т.п.);
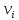, - сезонная компонента, отражающая повторяемость экономических процессов в течение не очень длительного пернода (года, иногда месяца, недели и т.д., например, объем продаж товаров или перевозок пассажиров в различные времена года);
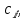- циклическая компонента, отражающая повторяемость экономических процессов в течение длительных периодов (например,Необходимо: а) найти парные, частные и множественный R, 12 коэффициенты корреляции между переменными и оценить их значимость на уровне а = 0,05; б) найти уравнение множественной регрессии Упо X1 и Х2, оценить значимость этого уравнения и его коэффициентов на уровне а = 0,05; в) сравнить раздельное влияние на зависимую переменную каждой из объясняющих переменных, используя стандартизованные коэффициенты регрессии и коэффициенты эластичности; г) найти 95%-ные доверительные интервалы для коэффициентов регрессии, а также для среднего и индивидуальных значений себестоимости одной тонны литья в цехах, в которых выработка литья на одного работающего составляет 40 т, а брак литья - 5%.
13.14. Имеются следующие данные о годовых ставках месячных доходов по трем акциям за шестимесячный период:
| Акция | Доходы оп месяцам, % | |||||
| A | 5,4 | 5,3 | 4,9 | 4,9 | 5,4 | 6,0 |
| B | 6,3 | 6,2 | 6,1 | 5,8 | 5,7 | 5,7 |
| C | 9,2 | 9,2 | 9,1 | 9,0 | 8,7 | 8,6 |
Есть основания предполагать, что доходы Y по акции С зависят от доходов
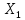и 
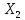по акциям А и В. Необходимо: а) составить уравнение регрессии Y по 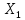и 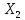; б) найти множественный коэффициент корреляции 
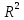и коэффициент детерминации R2 и пояснить их смысл; в) проверить на уровне а = 0,05 значимость полученного уравнения регрессии; г) оценить средний доход по акции С, если доходы по акциям А и В составили соответственно 5,5 и 6.0%.13.12. Распределение 50 гастрономических магазинов области по уровню издержек обращения X (%) и годовому объему товарооборота Y (млн руб. ) представлено в таблице:
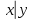 | 0,5 –2,0 | 2,0 –3,5 | 3,5 –5,0 | 5,0 – 6,5 | 6,5 – 8,0 | Итого |
| 4 – 6 | – | – | – | 3 | 2 | 5 |
| 6 – 8 | – | 4 | 8 | 8 | 1 | 21 |
| 8 –10 | 2 | 5 | 5 | 2 | – | 14 |
| 10 –12 | 3 | 1 | 5 | – | – | 9 |
| 12 –14 | 1 | – | – | – | – | 1 |
| Итого | 6 | 10 | 18 | 13 | 3 | 50 |
Необходимо: а) построить эмпирическую линию регрессии У по X; б) выровнять полученную зависимость по прямой и гиперболе и вычислить остаточную дисперсию для каждого случая; в) оценить тесноту связи между переменными с помощью эмпирического корреляционного отношения
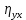, коэффициента корреляции r индекса корреляции 
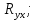проверить значимость 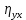и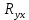 
и сравнить их по величине; г) на основании результатов, полученных в п. а), б), в), определить, какое из двух полученных уравнений регрессии целесообразнее использовать для исследования заданной зависимости.13.13. Имеются следующие данные о выработке литья на одного работающего
(т), браке литья 
(%) и себестоимости одной тонны литья Y (руб.) по 25 литейным цехам заводов:| i | 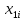 | 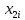 |  | i | 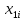| 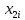| | i | | | |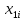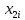
| 1 2 3 4 5 6 7 8 9 | 14,6 13,5 21,5 17,4 44,8 111,9 20,1 28,1 22,3 | 4,2 6,7 5,5 7,7 1,2 2,2 8,4 1,4 4,2 | 239 254 262 251 158 101 259 186 204 | 10 11 12 13 14 15 16 17 18 | 25,3 56,0 40,2 40,6 75,8 27,6 88,4 16,6 33,4 | 0,9 1,3 1,8 3,3 3,4 1,1 0,1 4,1 2,3 | 198 170 173 197 172 201 130 251 195 | 19 20 21 22 23 24 25 | 17,0 33,1 30,1 65,2 22,6 33,4 19,7 | 9,3 3,3 3,5 1,0 5,2 2,3 2,7 | 282 196 186 176 238 204 205 |
Итак, с помощью обратной матрицы
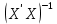определяется не только сам вектор b оценок параметров (13.28), но и дисперсии и ковариации его компонент.Входящая в выражение (13.36) дисперсия возмущений неизвестна. Заменив ее выборочной остаточной дисперсией
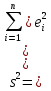
(13.37)
по формуле (13.36) получаем выборочную оценку ковариационной матрицы К. (В знаменателе выражения (13.37) стоит n - (р + 1), а не n - 2, как это было выше в формуле (13.6). Это связано с тем, что теперь р + 1 степеней свободы (а не две) теряются при определении неизвестных параметров, число которых вместе со свободным членом
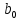равно р + 1.)13.7. Определение доверительных интервалов для коэффициентов и функции регрессии
Перейдем теперь к оценке значимости коэффициентов регрессии
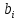и построению доверительного интервала для параметров регрессионной модели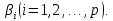 
В силу соотношений (13.34), (13.36) и изложенного выше оценка дисперсии коэффициента регрессии b, определится по формуле:
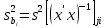,где
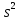- несмещенная оценка параметра 
;
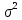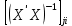- диагональный элемент матрицы 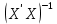.Среднее квадратическое отклонение (стандартная ошибка) коэффициента регрессии
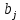примет вид: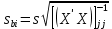
Оценка значимости коэффициента регрессии
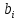означает проверку нуле-вой гипотезы о равенстве параметра
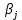множественной модели (13.22) нулю, т.е. 