Файл: Рис. 14. 1 Следует обратить внимание на то, что в отличие от е, первые три составляющие (компоненты) и,, v, с, являются закономерными, неслучайными..docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 53
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
= 0 против альтернативной гипотезы 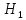 :
: 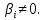
Эта проверка основана на том, что статистика (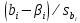 , имеет t-распределение Стьюдента с k = n - р - 1 степенями свободы. Поэтому
, имеет t-распределение Стьюдента с k = n - р - 1 степенями свободы. Поэтому  значимо отличается от нуля на уровне значимости а
значимо отличается от нуля на уровне значимости а
Рассматривая ковариационную матрицу К, легко заметить, что на ее главной диагонали находятся дисперсии оценок параметров регрессии, ибо
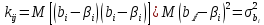 (13.34)
(13.34)
В сокращенном виде ковариационная матрица К имеет вид:
K = M[(b -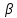 ) (b -
) (b - 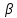 )']
)']
(в этом легко убедиться, перемножив векторы (b -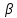 ) и (b -
) и (b - 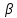 )'.
)'.
Учитывая (13.32), преобразуем это выражение:
K= M{[(X'X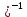 X'
X'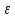 ] [(XX
] [(XX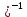 X'
X' 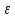 ]'}=
]'}=
= M[(X'X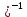 X'
X'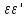 X(X
X(X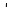 X
X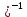 ]=(X'X
]=(X'X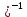 X'M(
X'M(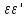 )X(X'X
)X(X'X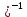 (13.35)
(13.35)
ибо элементы матрицы Х- неслучайные величины.
Матрица М(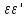 ) представляет собой ковариационную матрицу
) представляет собой ковариационную матрицу
вектора возмущений с:
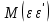 =
=
в которой все элементы, не лежащие на главной диагонали, равны нулю в силу предпосылки 4 о некоррелированности возмущений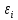 и
и 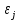 , между собой (см. (13.5)), а все элементы, лежащие на главной диагонали, в силу предпосылок 2 и 3 регрессионного анализа (см. (13.3) и (13.4)) равны одной и той же дисперсии
, между собой (см. (13.5)), а все элементы, лежащие на главной диагонали, в силу предпосылок 2 и 3 регрессионного анализа (см. (13.3) и (13.4)) равны одной и той же дисперсии 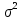 :
:
M(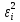 ) = M(
) = M(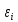 - 0)
- 0)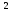 = D(
= D(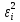 ) =
) =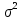
Поэтому матрица М( ) =
) = 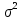 E, где Е - единичная матрица п-го порядка. Следовательно, в силу соотношения (13.35) ковариационная матрица вектора b оценок параметров:
E, где Е - единичная матрица п-го порядка. Следовательно, в силу соотношения (13.35) ковариационная матрица вектора b оценок параметров:
K = [(X'X X' (
X' (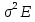 )]X (X'X
)]X (X'X  .=
.= 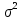 (X'X
(X'X  (X'EX
(X'EX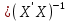 ,
,
или
K=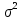 (X'X
(X'X . (13. 36)
. (13. 36)
добычу угля большее влияние оказывает фактор «мощность пласта» по сравнению с фактором «уровень механизации работ».
Преобразуем вектор оценок (13.28) с учетом формулы (13.23):
b = (X'X X'(X
X'(X +
+
) = (X'X (X'X)
(X'X)  +(X'X
+(X'X X'
X'  =
=
= E + (X'X
+ (X'X X'
X' 
или
b = + (X'X
+ (X'X X'
X'  . (13. 32)
. (13. 32)
т.е. оценки параметров (13.28), найденные по выборке, будут содержать случайные ошибки.
13.6. Ковариационная матрица и ее выборочная оценка
Вариации оценок параметров будут в конечном счете определять точность уравнения множественной регрессии. Для их измерения в многомерном регрессионном анализе рассматривают так называемую ковариационную матрицу К, являющуюся матричным аналогом дисперсии одной переменной:
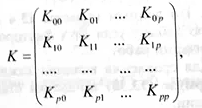
где элементы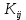 - ковариации (или корреляционные моменты) оценок параметров
- ковариации (или корреляционные моменты) оценок параметров 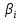 и
и  (i, j = 0, 1, …, р). Ковариация двух переменных определяется как математическое ожидание произведения отклонений этих переменных от их математических ожиданий (см. § 5.6). Поэтому
(i, j = 0, 1, …, р). Ковариация двух переменных определяется как математическое ожидание произведения отклонений этих переменных от их математических ожиданий (см. § 5.6). Поэтому
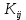 = M [(
= M [( - M (
- M ( ))(
))(  - M(
- M( ))]. (13. 33)
))]. (13. 33)
Ковариация характеризует как степень рассеяния значений двух переменных относительно их математических ожиданий, так и взаимосвязь этих переменных.
В силу того, что оценки , полученные методом наименьших квадратов, являются несмещенными оценками параметров
, полученные методом наименьших квадратов, являются несмещенными оценками параметров
 , т.е.
, т.е.
M( )
) 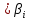 , выражение (13.33) примет вид:
, выражение (13.33) примет вид:
 = M [(
= M [( -
-  )(
)(  -
-  )].
)].
зависимой переменной Y при изменении на единицу объясняющей переменной в чистом виде, независимо от
в чистом виде, независимо от  . В случае парной регрессии
. В случае парной регрессии 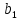 учитывает воздействие на У не только переменной
учитывает воздействие на У не только переменной  , но н косвенно корреляционно связанной с ней переменной
, но н косвенно корреляционно связанной с ней переменной  .
.
На практике часто бывает необходимо сравнение влияния на зависимую переменную различных объясняющих переменных, когда последние выражаются разными единицами измерения. В этом случае используют стандартизованные коэффициенты регрессии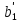 и коэффициенты эластичности
и коэффициенты эластичности 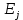 (j = 1, 2, … p):
(j = 1, 2, … p):
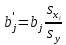
(13. 30)
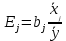
(13. 31)
Стандартизованный коэффициент регрессии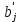 показывает, на сколько величин
показывает, на сколько величин 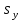 изменится в среднем зависимая переменная Y при увеличении только j-й объясняющей переменной на
изменится в среднем зависимая переменная Y при увеличении только j-й объясняющей переменной на 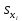 , а коэффициент эластичности
, а коэффициент эластичности 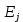 , - на сколько процентов (от средней) изменится в среднем У при увеличении только Х на 1%.
, - на сколько процентов (от средней) изменится в среднем У при увеличении только Х на 1%.
Пример 13.5. По данным примера 13.4
сравнить раздельное влияние на сменную добычу угля двух факторов - мощности пласта и уровня механизации работ.
Р е ш е н и е. Для сравнения влияния каждой из объясняющих переменных по формуле (13.30) вычислим стандартизованные коэффициенты регрессии:
 = 0,8539.13
= 0,8539.13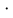
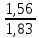 = 0,728;
= 0,728;  = 0,3670
= 0,3670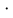
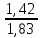 =0,285,
=0,285,
а по формуле (13.31) - коэффициенты эластичности:
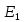 , = 0,8539
, = 0,8539 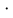
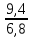 = 1,180;
= 1,180; 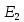 = 0,3670
= 0,3670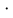
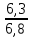 = 0,340.
= 0,340.
(Здесь мы опустили расчет необходимых характеристик переменных:
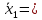 9,4;
9,4; 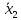 = 6,3;
= 6,3; 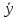 = 6,8;
= 6,8; 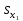 = 1,56;
= 1,56; 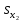 = 1,42;
= 1,42; 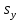 =1,83.)
=1,83.)
Таким образом, увеличение мощности пласта и уровня механизации работ только на одно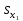 или на одно
или на одно 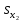 увеличивает в среднем сменную добычу угля на одного рабочего соответственно на 0,728
увеличивает в среднем сменную добычу угля на одного рабочего соответственно на 0,728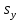 , или на 0,285
, или на 0,285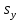 , а увеличение этих переменных на 1% (от своих средних значений) приводит в среднем к росту добычи угля соответственно на 1,18% и 0,34%. Итак, по обоим показателям на сменную
, а увеличение этих переменных на 1% (от своих средних значений) приводит в среднем к росту добычи угля соответственно на 1,18% и 0,34%. Итак, по обоим показателям на сменную
Теперь
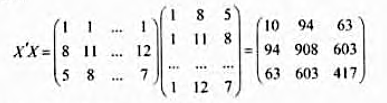
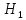 :
: 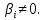
Эта проверка основана на том, что статистика (
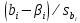 , имеет t-распределение Стьюдента с k = n - р - 1 степенями свободы. Поэтому
, имеет t-распределение Стьюдента с k = n - р - 1 степенями свободы. Поэтому  значимо отличается от нуля на уровне значимости а
значимо отличается от нуля на уровне значимости аРассматривая ковариационную матрицу К, легко заметить, что на ее главной диагонали находятся дисперсии оценок параметров регрессии, ибо
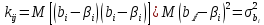 (13.34)
(13.34)В сокращенном виде ковариационная матрица К имеет вид:
K = M[(b -
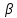 ) (b -
) (b - 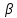 )']
)'](в этом легко убедиться, перемножив векторы (b -
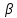 ) и (b -
) и (b - 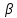 )'.
)'.Учитывая (13.32), преобразуем это выражение:
K= M{[(X'X
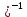 X'
X'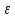 ] [(XX
] [(XX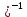 X'
X' 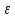 ]'}=
]'}== M[(X'X
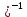 X'
X'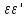 X(X
X(X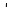 X
X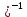 ]=(X'X
]=(X'X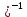 X'M(
X'M(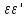 )X(X'X
)X(X'X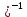 (13.35)
(13.35)ибо элементы матрицы Х- неслучайные величины.
Матрица М(
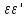 ) представляет собой ковариационную матрицу
) представляет собой ковариационную матрицувектора возмущений с:
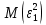 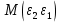 … 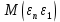 | 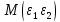 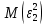 … 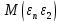 | … … … … | 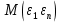 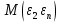 … 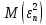 |
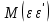 =
=в которой все элементы, не лежащие на главной диагонали, равны нулю в силу предпосылки 4 о некоррелированности возмущений
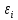 и
и 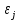 , между собой (см. (13.5)), а все элементы, лежащие на главной диагонали, в силу предпосылок 2 и 3 регрессионного анализа (см. (13.3) и (13.4)) равны одной и той же дисперсии
, между собой (см. (13.5)), а все элементы, лежащие на главной диагонали, в силу предпосылок 2 и 3 регрессионного анализа (см. (13.3) и (13.4)) равны одной и той же дисперсии 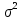 :
:M(
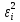 ) = M(
) = M(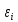 - 0)
- 0)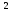 = D(
= D(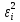 ) =
) =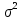
Поэтому матрица М(
 ) =
) = 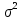 E, где Е - единичная матрица п-го порядка. Следовательно, в силу соотношения (13.35) ковариационная матрица вектора b оценок параметров:
E, где Е - единичная матрица п-го порядка. Следовательно, в силу соотношения (13.35) ковариационная матрица вектора b оценок параметров:K = [(X'X
 X' (
X' (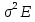 )]X (X'X
)]X (X'X  .=
.= 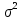 (X'X
(X'X  (X'EX
(X'EX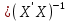 ,
,или
K=
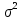 (X'X
(X'X . (13. 36)
. (13. 36)добычу угля большее влияние оказывает фактор «мощность пласта» по сравнению с фактором «уровень механизации работ».
Преобразуем вектор оценок (13.28) с учетом формулы (13.23):
b = (X'X
 X'(X
X'(X +
+
) = (X'X
 (X'X)
(X'X)  +(X'X
+(X'X X'
X'  =
== E
 + (X'X
+ (X'X X'
X' 
или
b =
 + (X'X
+ (X'X X'
X'  . (13. 32)
. (13. 32)т.е. оценки параметров (13.28), найденные по выборке, будут содержать случайные ошибки.
13.6. Ковариационная матрица и ее выборочная оценка
Вариации оценок параметров будут в конечном счете определять точность уравнения множественной регрессии. Для их измерения в многомерном регрессионном анализе рассматривают так называемую ковариационную матрицу К, являющуюся матричным аналогом дисперсии одной переменной:
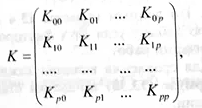
где элементы
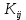 - ковариации (или корреляционные моменты) оценок параметров
- ковариации (или корреляционные моменты) оценок параметров 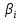 и
и  (i, j = 0, 1, …, р). Ковариация двух переменных определяется как математическое ожидание произведения отклонений этих переменных от их математических ожиданий (см. § 5.6). Поэтому
(i, j = 0, 1, …, р). Ковариация двух переменных определяется как математическое ожидание произведения отклонений этих переменных от их математических ожиданий (см. § 5.6). Поэтому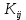 = M [(
= M [( - M (
- M ( ))(
))(  - M(
- M( ))]. (13. 33)
))]. (13. 33)Ковариация характеризует как степень рассеяния значений двух переменных относительно их математических ожиданий, так и взаимосвязь этих переменных.
В силу того, что оценки
 , полученные методом наименьших квадратов, являются несмещенными оценками параметров
, полученные методом наименьших квадратов, являются несмещенными оценками параметров
 , т.е.
, т.е.M(
 )
) 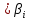 , выражение (13.33) примет вид:
, выражение (13.33) примет вид: = M [(
= M [( -
-  )(
)(  -
-  )].
)].зависимой переменной Y при изменении на единицу объясняющей переменной
 в чистом виде, независимо от
в чистом виде, независимо от  . В случае парной регрессии
. В случае парной регрессии 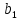 учитывает воздействие на У не только переменной
учитывает воздействие на У не только переменной  , но н косвенно корреляционно связанной с ней переменной
, но н косвенно корреляционно связанной с ней переменной  .
. На практике часто бывает необходимо сравнение влияния на зависимую переменную различных объясняющих переменных, когда последние выражаются разными единицами измерения. В этом случае используют стандартизованные коэффициенты регрессии
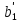 и коэффициенты эластичности
и коэффициенты эластичности 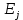 (j = 1, 2, … p):
(j = 1, 2, … p):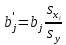
(13. 30)
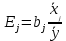
(13. 31)
Стандартизованный коэффициент регрессии
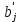 показывает, на сколько величин
показывает, на сколько величин 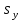 изменится в среднем зависимая переменная Y при увеличении только j-й объясняющей переменной на
изменится в среднем зависимая переменная Y при увеличении только j-й объясняющей переменной на 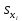 , а коэффициент эластичности
, а коэффициент эластичности 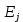 , - на сколько процентов (от средней) изменится в среднем У при увеличении только Х на 1%.
, - на сколько процентов (от средней) изменится в среднем У при увеличении только Х на 1%.Пример 13.5. По данным примера 13.4
сравнить раздельное влияние на сменную добычу угля двух факторов - мощности пласта и уровня механизации работ.
Р е ш е н и е. Для сравнения влияния каждой из объясняющих переменных по формуле (13.30) вычислим стандартизованные коэффициенты регрессии:
 = 0,8539.13
= 0,8539.13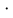
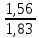 = 0,728;
= 0,728; 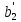 = 0,3670
= 0,3670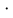
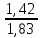 =0,285,
=0,285, а по формуле (13.31) - коэффициенты эластичности:
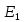 , = 0,8539
, = 0,8539 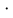
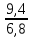 = 1,180;
= 1,180; 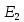 = 0,3670
= 0,3670
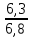 = 0,340.
= 0,340.(Здесь мы опустили расчет необходимых характеристик переменных:
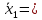 9,4;
9,4; 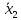 = 6,3;
= 6,3; 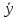 = 6,8;
= 6,8; 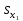 = 1,56;
= 1,56; 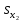 = 1,42;
= 1,42; 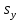 =1,83.)
=1,83.) Таким образом, увеличение мощности пласта и уровня механизации работ только на одно
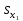 или на одно
или на одно 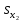 увеличивает в среднем сменную добычу угля на одного рабочего соответственно на 0,728
увеличивает в среднем сменную добычу угля на одного рабочего соответственно на 0,728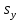 , или на 0,285
, или на 0,285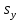 , а увеличение этих переменных на 1% (от своих средних значений) приводит в среднем к росту добычи угля соответственно на 1,18% и 0,34%. Итак, по обоим показателям на сменную
, а увеличение этих переменных на 1% (от своих средних значений) приводит в среднем к росту добычи угля соответственно на 1,18% и 0,34%. Итак, по обоим показателям на сменнуюТеперь
