Файл: Рис. 14. 1 Следует обратить внимание на то, что в отличие от е, первые три составляющие (компоненты) и,, v, с, являются закономерными, неслучайными..docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 54
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(см. суммы в итоговой строке табл. 13.7);
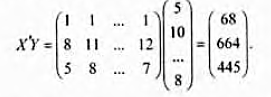
Матрицу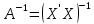 определим по формуле
определим по формуле 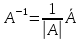 , где
, где  - определитель матрицы X’X ,
- определитель матрицы X’X , 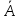 - матрица, присоединенная к матрице X’X . Получим (рекомендуем читателю убедиться в этом самостоятельно)
- матрица, присоединенная к матрице X’X . Получим (рекомендуем читателю убедиться в этом самостоятельно)
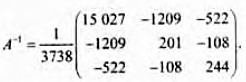
Теперь в соответствии с формулой (13.28), умножая эту матрицу на вектор
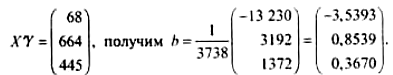
С учетом равенства (13.29) уравнение множественной регрессии имеет вид: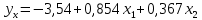 . Оно показывает, что при увеличении только мощности пласта
. Оно показывает, что при увеличении только мощности пласта  (при неизменном
(при неизменном  ) на 1 м, добыча угля на одного рабочего увеличивается в среднем на 0,854 т, а при увеличении только уровня механизации работ
) на 1 м, добыча угля на одного рабочего увеличивается в среднем на 0,854 т, а при увеличении только уровня механизации работ  (при неизменной
(при неизменной  ) - в среднем на 0,367 т.
) - в среднем на 0,367 т.
Добавление в регрессионную модель новой объясняющей переменной изменило коэффициент регрессии
изменило коэффициент регрессии  (Y по
(Y по  ) с 1,016 для парной регрессии (см. пример 13.1) до 0.854 - для множественной регрессии. В этом никакого противоречия нет, так как во втором случае коэффициент регрессии позволяет оценить прирост
) с 1,016 для парной регрессии (см. пример 13.1) до 0.854 - для множественной регрессии. В этом никакого противоречия нет, так как во втором случае коэффициент регрессии позволяет оценить прирост
Пример 13.4. Имеются следующие данные' (условные) о сменной добыче угля на одного рабочего Y (т), мощности пласта (м) и уровне механизации работ
(м) и уровне механизации работ  (%), характеризующие процесс добычи угля в 10 шахтах (табл. 13.6).
(%), характеризующие процесс добычи угля в 10 шахтах (табл. 13.6).
Таблица 13.6
Предполагая, что между переменными Y, и
и  существует линейная корреляционная зависимость, найти ее аналитическое выражение (уравнение регрессии Y по
существует линейная корреляционная зависимость, найти ее аналитическое выражение (уравнение регрессии Y по  и
и 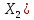
Р е ш е н и е. Обозначим
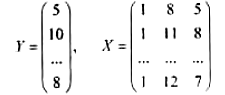
(напоминаем, что в матрицу плана Х вводится дополнительный столбец чисел, состоящий из единиц). Для удобства вычислений составляем вспомогательную таблицу (табл. 13.7).
В этом примере использованы данные примера 13.1 с добавлением результатов наблюдений над новой объясняющей переменной , при этом старую переменную Х из примера 13.1 обозначаем теперь
, при этом старую переменную Х из примера 13.1 обозначаем теперь 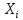 .
.

Матрицу
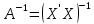 определим по формуле
определим по формуле 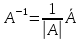 , где
, где  - определитель матрицы X’X ,
- определитель матрицы X’X ,  - матрица, присоединенная к матрице X’X . Получим (рекомендуем читателю убедиться в этом самостоятельно)
- матрица, присоединенная к матрице X’X . Получим (рекомендуем читателю убедиться в этом самостоятельно)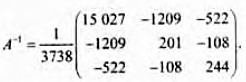
Теперь в соответствии с формулой (13.28), умножая эту матрицу на вектор
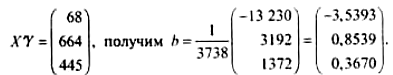
С учетом равенства (13.29) уравнение множественной регрессии имеет вид:
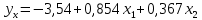 . Оно показывает, что при увеличении только мощности пласта
. Оно показывает, что при увеличении только мощности пласта  (при неизменном
(при неизменном  ) на 1 м, добыча угля на одного рабочего увеличивается в среднем на 0,854 т, а при увеличении только уровня механизации работ
) на 1 м, добыча угля на одного рабочего увеличивается в среднем на 0,854 т, а при увеличении только уровня механизации работ  (при неизменной
(при неизменной  ) - в среднем на 0,367 т.
) - в среднем на 0,367 т.Добавление в регрессионную модель новой объясняющей переменной
 изменило коэффициент регрессии
изменило коэффициент регрессии  (Y по
(Y по  ) с 1,016 для парной регрессии (см. пример 13.1) до 0.854 - для множественной регрессии. В этом никакого противоречия нет, так как во втором случае коэффициент регрессии позволяет оценить прирост
) с 1,016 для парной регрессии (см. пример 13.1) до 0.854 - для множественной регрессии. В этом никакого противоречия нет, так как во втором случае коэффициент регрессии позволяет оценить приростПример 13.4. Имеются следующие данные' (условные) о сменной добыче угля на одного рабочего Y (т), мощности пласта
 (м) и уровне механизации работ
(м) и уровне механизации работ  (%), характеризующие процесс добычи угля в 10 шахтах (табл. 13.6).
(%), характеризующие процесс добычи угля в 10 шахтах (табл. 13.6).
Таблица 13.6
| i | 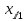 | 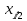 | 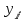 | 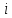 | 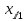 | 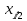 | 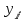 |
| 1 | 8 | 5 | 5 | 6 | 8 | 8 | 6 |
| 2 | 11 | 8 | 10 | 7 | 9 | 6 | 6 |
| 3 | 12 | 8 | 10 | 8 | 9 | 4 | 5 |
| 4 | 9 | 5 | 7 | 9 | 8 | 5 | 6 |
| 5 | 8 | 7 | 5 | 10 | 12 | 7 | 8 |
Предполагая, что между переменными Y,
 и
и  существует линейная корреляционная зависимость, найти ее аналитическое выражение (уравнение регрессии Y по
существует линейная корреляционная зависимость, найти ее аналитическое выражение (уравнение регрессии Y по  и
и 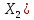
Р е ш е н и е. Обозначим
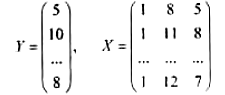
(напоминаем, что в матрицу плана Х вводится дополнительный столбец чисел, состоящий из единиц). Для удобства вычислений составляем вспомогательную таблицу (табл. 13.7).
| i | 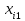 | 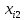 | 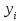 | 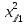 | 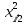 | 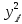 | 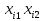 | 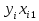 | 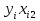 | 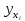 | 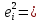 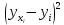 |
| 1 | 8 | 5 | 5 | 64 | 25 | 25 | 40 | 40 | 25 | 5,13 | 0,016 |
| 2 | 11 | 8 | 10 | 121 | 64 | 100 | 88 | 110 | 80 | 8,79 | 1,464 |
| 3 | 12 | 8 | 10 | 144 | 64 | 100 | 96 | 120 | 80 | 9,64 | 1,127 |
| 4 | 9 | 5 | 7 | 81 | 25 | 49 | 45 | 63 | 35 | 5,98 | 1,038 |
| 5 | 8 | 7 | 5 | 64 | 49 | 25 | 56 | 40 | 35 | 5,86 | 0,741 |
| 6 | 8 | 8 | 6 | 64 | 64 | 36 | 64 | 48 | 48 | 6,23 | 0,052 |
| 7 | 9 | 6 | 6 | 81 | 36 | 36 | 54 | 54 | 36 | 6,35 | 0,121 |
| 8 | 9 | 4 | 5 | 81 | 16 | 25 | 36 | 45 | 20 | 5.61 | 0,377 |
| 9 | 8 | 5 | 6 | 64 | 25 | 36 | 40 | 48 | 30 | 5,31 | 0,762 |
| 10 | 12 | 7 | 8 | 144 | 49 | 64 | 84 | 96 | 56 | 9,28 | 1,631 |
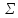 | 94 | 63 | 68 | 908 | 417 | 496 | 603 | 664 | 445 | - | 6,329 |
В этом примере использованы данные примера 13.1 с добавлением результатов наблюдений над новой объясняющей переменной
 , при этом старую переменную Х из примера 13.1 обозначаем теперь
, при этом старую переменную Х из примера 13.1 обозначаем теперь 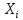 .
.