Файл: Исследование движения тела под действием квазиупругой силы. Выбор физических моделей для анализа движения тел.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 84
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Коломиец Александр
Группа: 11002218
1.7. Свободные механические колебания
Введение:
Ознакомьтесь с конспектом лекций и учебником. Запустите программу компьютерного моделирования. Выберите модель «Математический маятник с затуханием», потом модель «Пружинный маятник с затуханием». Прочитайте краткие теоретические сведения. Оформите конспект.
Цель работы:
-
Исследование движения тела под действием квазиупругой силы. -
Выбор физических моделей для анализа движения тел. -
Экспериментальное определение зависимости частоты колебаний от параметров системы.
Краткая теория:
| Механическое колебание – периодически повторяющееся движение тела. Период T – минимальное время, через которое движение полностью повторяется. Полное колебание – минимальная часть периодического процесса, которая полностью повторяется. Гармоническое колебание – движение, при котором координата тела меняется со временем по гармоническому закону (синуса или косинуса), например
Основными характеристиками гармонических колебаний являются: Амплитуда xm – максимальное значение смещения (координаты) х. Циклическая частота колебаний (ω0) есть характеристика колебаний, в 2π раз большая обычной или линейной частоты. Линейная частота (ν) есть число полных колебаний за единицу времени ν = 1/Т. Фаза (ω0t + φ0) – значение аргумента гармонической функции в момент t. Начальная фаза φ0 – значение аргумента гармонической функции при t = 0. Свободными называются колебания, происходящие в системе тел, на которую не действуют внешние силы. |
Вынужденными называются колебания, происходящие в системе тел под действием внешней силы.
Дифференциальное уравнение
свободных гармонических колебаний:
| d2xdt2+const⋅x=0. |
Его решением является гармоническая функция
| x (t)=xmcos(ω0t+φ0), |
причем только частота колебаний может быть определена из дифференциального уравнения:
| ω0=const. |
Амплитуда и начальная фаза определяются из дополнительных данных (например, из начального смещения и скорости).
Дифференциальное уравнение свободных затухающих колебаний
| d2xdt2+2βdxdt+ω02x=0, |
где β – коэффициент затухания.
Его решением является произведение двух функций
| x (t)=xme-βtcos(ω0t+φ0). |
Математический маятник (ММ) и пружинный маятник (ПМ) – это модели некоторых систем, в которых могут происходить гармонические колебания.
ММ – это материальная точка, подвешенная на идеальной (невесомой и нерастяжимой) нити.
ПМ – это материальная точка, прикрепленная к идеальной (невесомой и подчиняющейся закону Гука) пружине. Формулы для ω0 в этих системах выпишите из конспекта или учебника.
Методика и порядок измерений:
Внимательно рассмотрите рисунки, найдите все регуляторы и другие элементы. Зарисуйте регуляторы соответствующих параметров и укажите, что они регулируют.
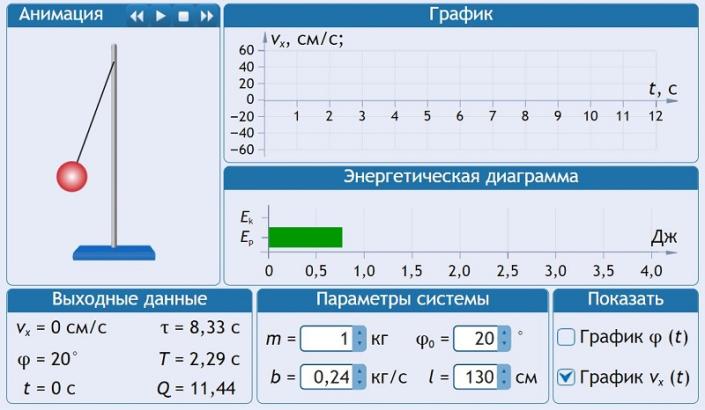
Выберите модель «Математический маятник с затуханием» (рис.1). Установите с помощью кнопок регуляторов максимальную длину нити L и значения коэффициента затухания b и начального угла φ0, указанные в табл. 1 для вашей бригады.
Щёлкая мышью кнопку Пуск (средняя часть кнопки управления), следите за движением точки на графиках угла и скорости и за поведением маятника. Потренируйтесь, останавливая движение (например, в максимуме смещения) кнопкой
Пауза (средняя часть кнопки управления) и запуская далее кнопкой Пуск. Выберите число полных колебаний N = 3–5 и измерьте их продолжительность Δt. Нажмите Сброс (нижнюю часть кнопки управлении) и измените длину маятника на 20 см. Повторите измерения и найдите изменения параметров процесса. Запишите результат в конспект и объясните его.
Получите у преподавателя допуск для выполнения измерений.
Измерения:
Эксперимент 1
Приступайте к измерениям длительности Δt для N (3–5) полных колебаний, начиная с максимальной длины (130 см) нити маятника и уменьшая ее каждый раз на 5 см (до минимальной длины 90 см). Перед изменением параметров нажимайте Сброс (нижнюю часть кнопки управлении). Длину нити L и результаты измерений длительности Δt записывайте в табл. 2, образец которой приведен ниже.
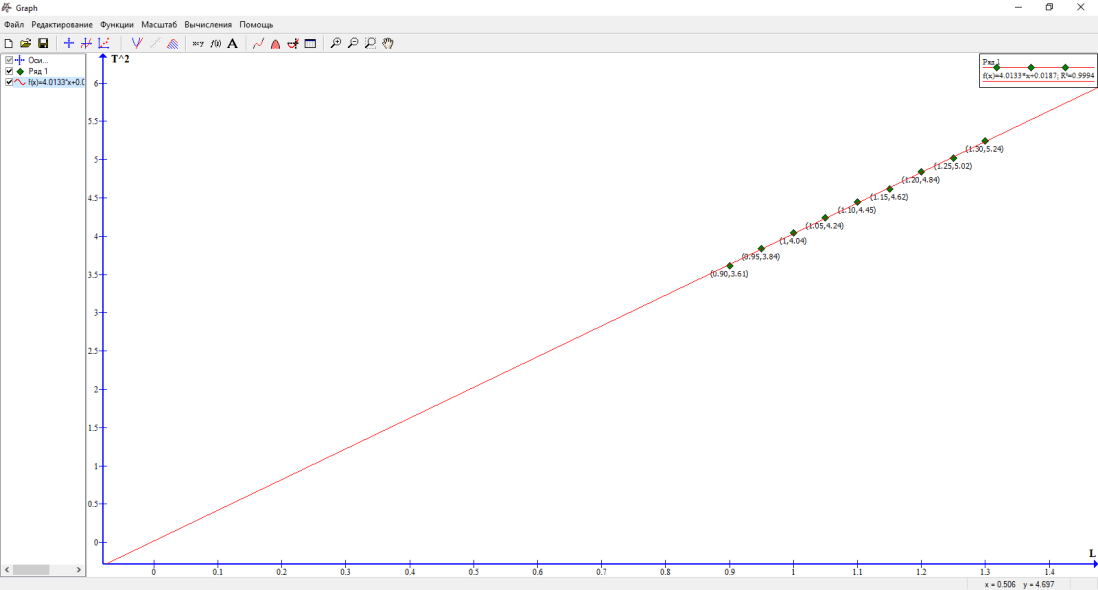
Таблица 3. Результаты измерений
| Номер измерения | N =5 | |||
| L, м | Δt, с | Т, с | Т2, с2 | |
| 1 | 1,3 | 11.5 | 2.29 | 5.24 |
| 2 | 1,25 | 11.2 | 2.24 | 5.02 |
| 3 | 1.20 | 11 | 2.2 | 4.84 |
| 4 | 1.15 | 10.7 | 2.15 | 4.62 |
| 5 | 1.10 | 10.6 | 2.11 | 4.45 |
| 6 | 1.05 | 10.3 | 2.06 | 4.24 |
| 7 | 1 | 10 | 2.01 | 4.04 |
| 8 | 0.95 | 9.8 | 1.96 | 3.84 |
| 9 | 0.90 | 9.3 | 1.9 | 3.61 |
| g, м/с2 | | 9,68 | | |


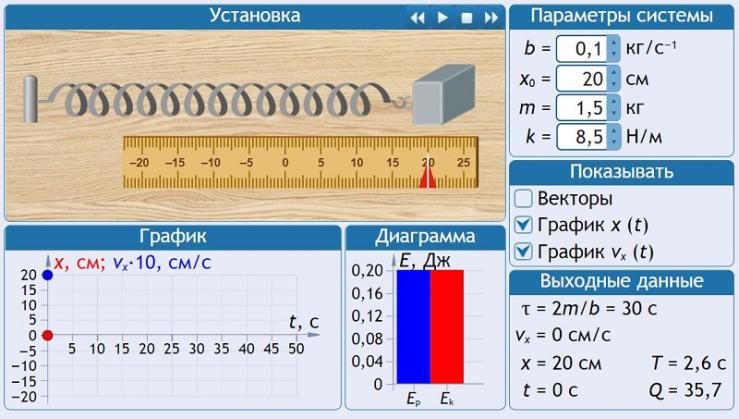
Эксперимент 2
Выберите модель «Пружинный маятник с затуханием» (рис. 2). Установите массу груза, значение коэффициента затухания и начальное смещение, указанные в табл. 1 для вашей бригады. Проведите измерения, аналогичные эксперименту 1, начав с минимального коэффициента жесткости k = 5 Н/м и увеличивая каждый раз на 1 Н/м.
Таблица 1 (в конспект не перерисовывать). Значения коэффициента затухания (вязкого трения), начального угла отклонения и массы
Таблица 4. Результаты измерений и расчетов
b=0.4 Xo=18 m=1
| Номер измерения | N =3 | ||||
| k, H/м | Δt, с | Т, с | ω, 1/с | ω2, 1/с2 | |
| 1 | 5 | 8.5 | 2.8 | 2.24 | 5.02 |
| 2 | 6 | 7.7 | 2.6 | 2.42 | 5.86 |
| 3 | 7 | 7.2 | 2.4 | 2.62 | 6.86 |
| 4 | 8 | 6.6 | 2.2 | 2.85 | 8.12 |
| 5 | 9 | 6.2 | 2.1 | 2.99 | 8.94 |
| 6 | 10 | 6 | 2 | 3.14 | 9.86 |