Задание 1 Решение задачи линейного программирования Фирма производит и продает два типа товаров. Фирма получает прибыль в размере c₁₌10 тыс.р. от производства и продажи каждой единицы товара 1 и в размере c₂₌5 тыс. р. от производства и продажи каждой единицы товара 2. Фирма состоит из трех подразделений. Затраты труда (чел.-дни) на производство этих товаров в каждом из подразделений указаны в таблице:

Подразделение	Трудозатраты, чел.-дней на 1 шт.
	Товар 1	Товар 2
1 2 3	5 2 5	3 2 4

Руководство рассчитало, что в следующем месяце фирма будет располагать следующими возможностями обеспечения производства трудозатратами: D₁₌1000 чел.-дней в подразделении 1, D₂₌600 — в подразделении 2 и D₃₌1900 — в подразделении 3. Составить задачу линейного программирования и найти ее решение графо-аналитическим методом. Определить максимальное значение целевой функции. Подтвердить решение в среде MSExcel.Решение:Для решения задачи необходимо составить математическую модель.Пусть X_1- количество товара 1; X₂-количество товара 2Целевая функция будет равна: 10X₁+5X₂ max;Система линейных неравенств примет вид: 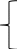5x₁+3x_2≤ 10002x₁+2x_{2 ≤}600 5x₁+4x₂ ≤ 1900Введем ограничения переменных: x_{1,2 ≥ 0;} x_1,2 – целое числоПостроим граничные прямые. Для это необходимо преобразовать систему линейных неравенств в равенства и для каждого равенства найти точки, для построения прямой.Система примет вид:

---

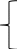
5x₁+3x_{2 =} 1000

2x₁+2x_{2 =} 600

5x₁+4x₂ = 1900

Для нахождения координат прямых поочередно приравняем x₁ и x₂ для каждого равенства к 0.

Получим:
5x₁+3x_{2 =} 1000; 1) (0;1000/3); 2) (200;0)

2x₁+2x_{2 =} 600; 1) (0;300); 2) (300;0)

5x₁+4x₂ = 1900; 1) (0;475); 2) (380;0)

Построим прямые на координатной плоскости:

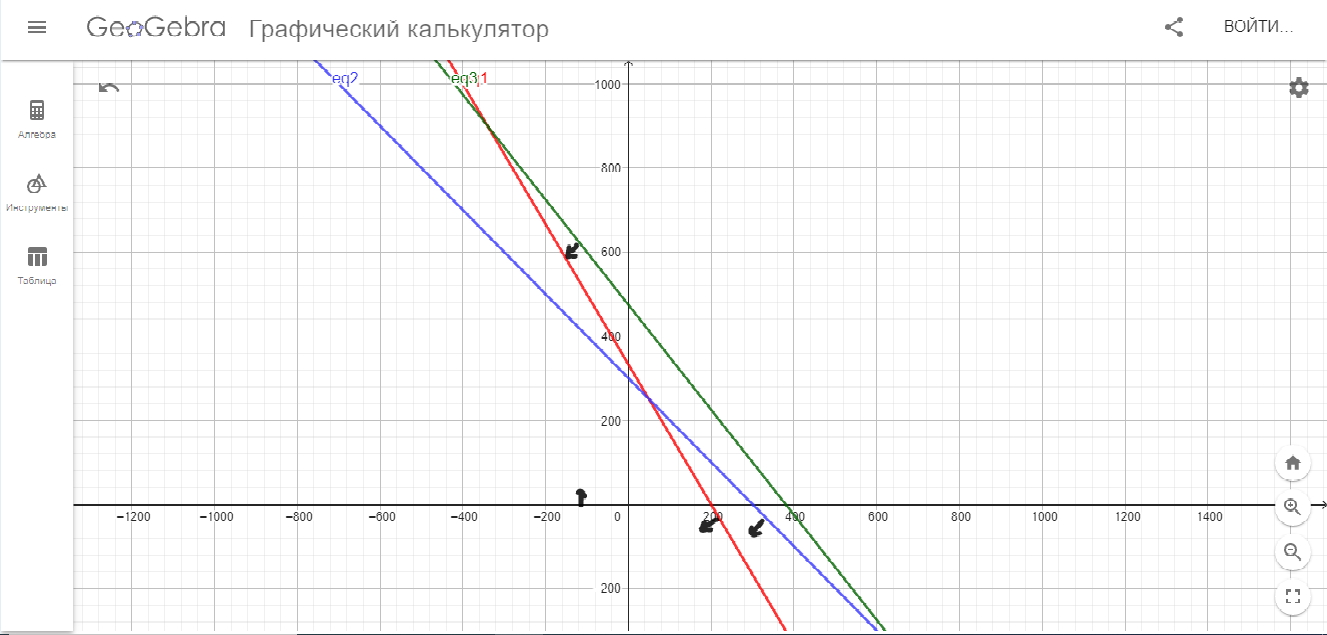Рис 1.Построение прямых
Для того, чтобы определить нужную область допустимых решений(ОДР) необходимо выбрать произвольным образом точку на плоскости, и ее координаты подставить в неравенства. Если неравенство выполняется при подстановке - штрихуем ту область, в которой расположена точка, если не выполняется-штрихуем область над прямой .

Возьмем точку Е(10;5).



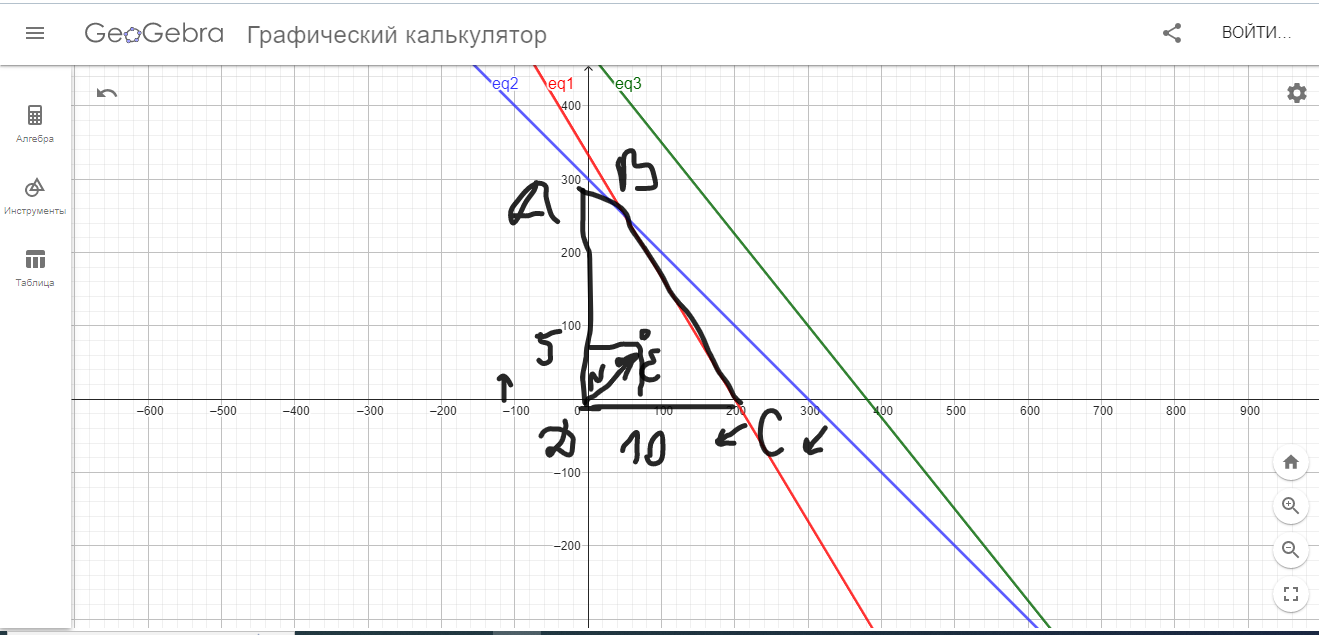
Рис 2.Определение ОДР
Подставив значения точки Е(10;5) в неравенства, определяем область допустимых решений- многоугольник АВСД.

Выполняем построение вектора нормали(N) от точки пересечения осей координатной плоскости до точки Е.

Максимальное или минимальное значение функция принимает только в вершинах области. Это точки с координатами: Д(0;0), А(0;300), С(200;0)

Координаты точки В - это пересечение двух прямых, заданных уравнениями.

Произведя вычисления получаем координаты: В(50;250).

Вычисляем целевую функцию для каждой точки:

Для точки А(0;300): F(X)=10*0+5*300=1500

Для точки C(200;0): F(X)=10*200+5*0=2000

Для точки B(50;250): F(X)=10*50+5*250=1750

Подтвердим решение в среде MSExcel:



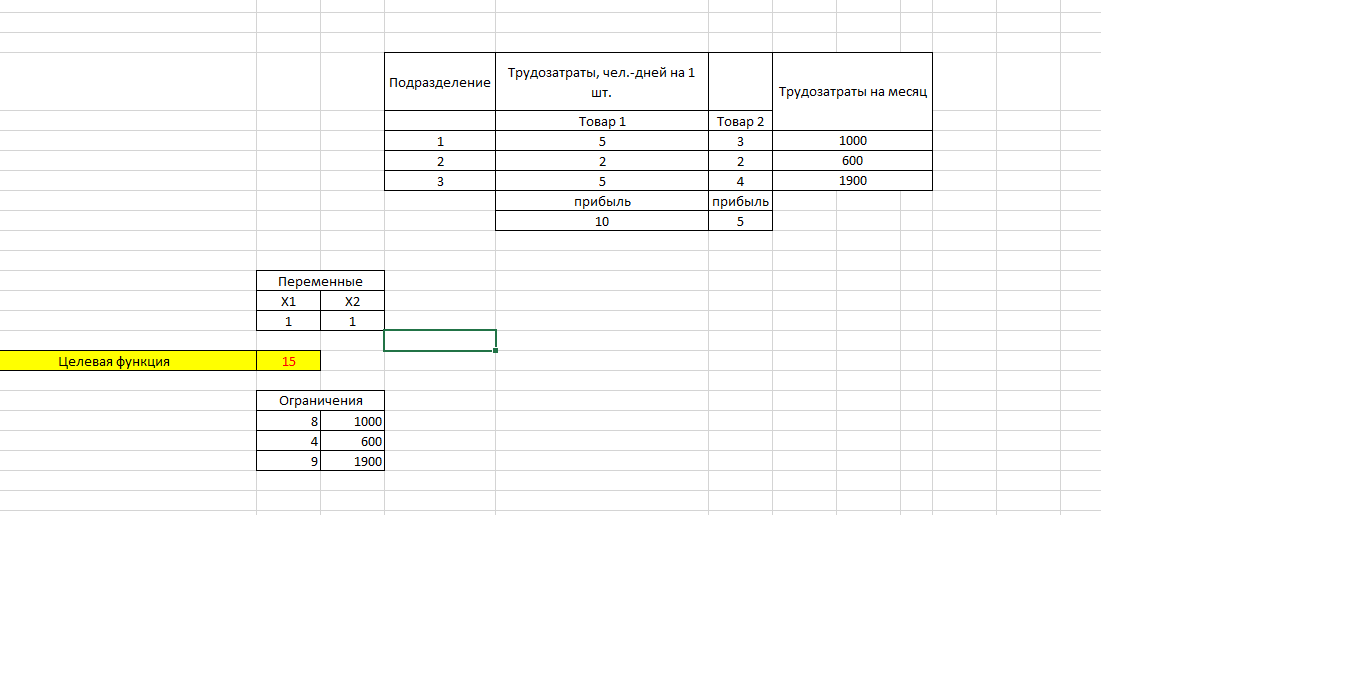
Рис 1. Данные для расчета задания 1

Использовалась надстройка «Поиск решений» с параметрами, приведенными на рисунке 2.


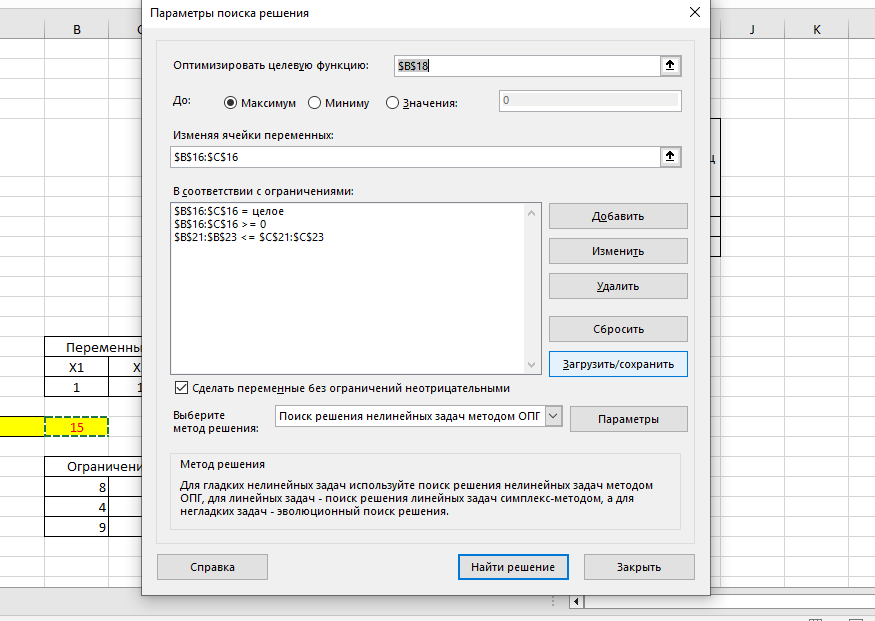
Рисунок 2. Параметры надстройки «Поиск решений».

Полученные результаты приведены на рисунке 3.

---

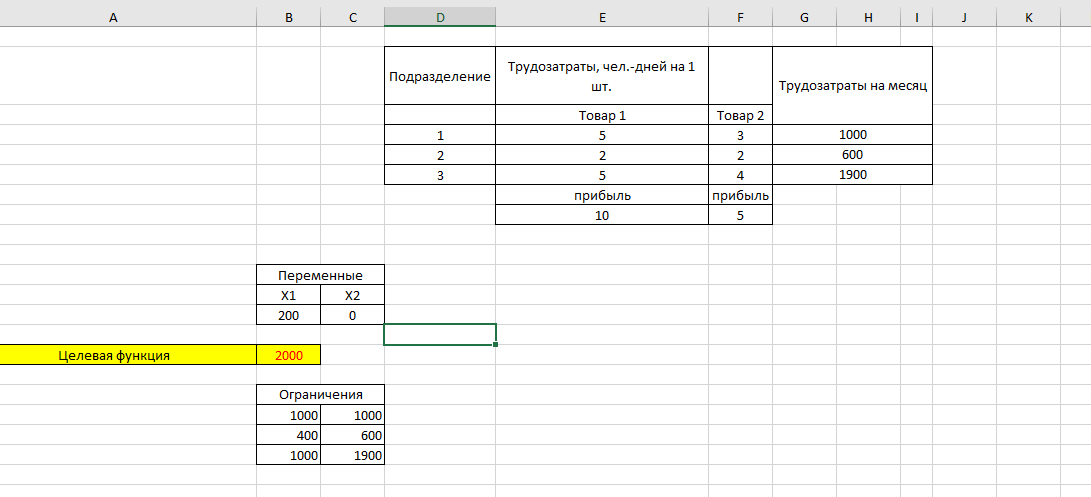
Рисунок 3. Результаты расчета после запуска надстройки «Поиск решений».Решение задачи: Переменные равны Х1 = 200, Х2 = 0. Значение целевой = 2000 Задание 2 Решение транспортной задачиНа трех элеваторах хранится зерно, часть которого нужно развезти по четырем хлебозаводам. 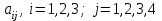— затраты на перевозку 1 тонны зерна с i-го элеватора на j-й хлебозавод.Составить план перевозки зерна, чтобы суммарные затраты на перевозку были минимальными.Решить транспортную задачу с использованием известных методов:- поиск опорного плана – методом Северо-Западного угла и методом минимального элемента;- поиск оптимального решения – методом потенциалов;- также представить результат, полученный в среде MSExcel.

Номер элеватора	Кол-во зерна на элеваторе (тыс. т)	Хлебозаводы и их потребность в зерне (тыс. т)
		1	2	3	4
		150	300	200	250
1	250	5	2	9	4
2	350	9	1	6	9
3	300	5	3	2	1

Решение:Перед тем как приступить к решению задачи, необходимо проверить условие баланса.Вычисляем суммарное количество зерна, имеющегося на элеваторе:S=250+350+300=900 тыс.т.Вычисляем суммарное количество потребностей:S=150+300+200+250=900В данном случае кол-во запасов равно кол-ву заявок потребителей, следовательно условие баланса выполняется, задача является закрытой.Приступим к нахождению опорного плана методом «северо-западного угла».В ячейку F11 («северо-западная» клетка) поставим максимальное значение, тем самым удовлетворив заявку первого потребителя. Тогда перевозки в пунктах В

---

₁ от других поставщиков должны быть равны нулю. Первый столбец оказался заполненным. Переходим к заполнению следующей «северо-западной» клетки G₁₁, учитывая, что запас поставщика  А₁ уменьшился на 150 и стал равен 100 ед. В ячейку G₁₁ поставим перевозку, равную 100 . Тогда перевозки из пункта А₁ остальным потребителям должны быть равны нулю. Первая строка оказалась заполненной. Переходим к заполнению следующей «северо-западной» клетки G_12..Учитывая, что заявка потребителя В₂ частично удовлетворена поставщиком А_1, оставшиеся 200 тыс.т. зерна удовлетворяем за счет поставщика А₂. Соответственно перевозка от поставщика А₃ потребителю В₂ должна равняться нулю. Второй столбец оказался заполненным. Продолжая этот процесс дальше, получим план перевозок, представленный на рис. 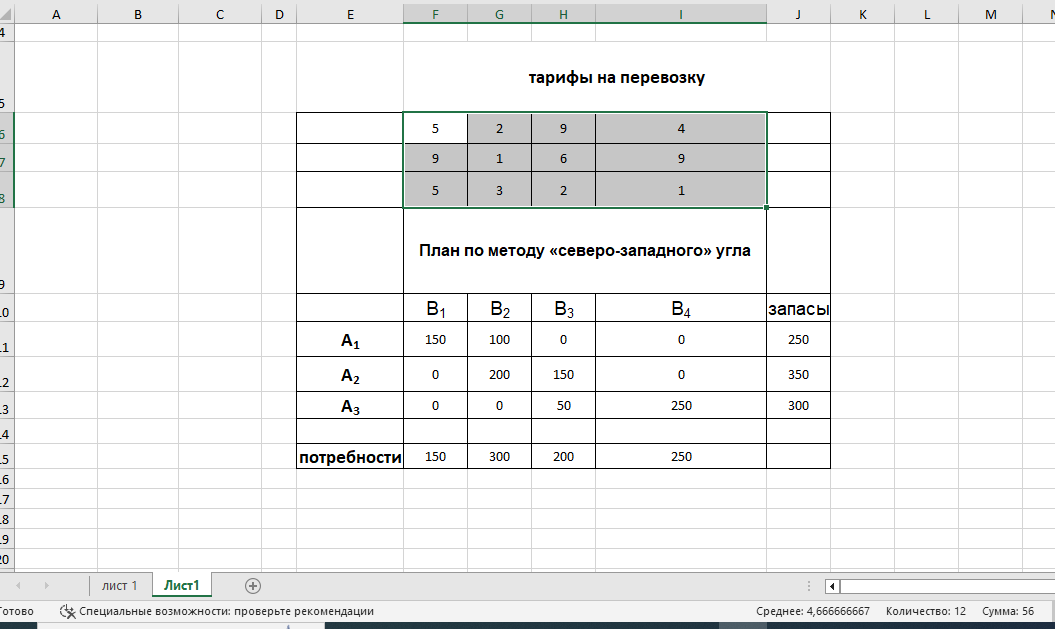1.Рис.1 План перевозок по методу «северо-западного угла»Теперь нужно посчитать стоимость начального опорного решения. Для этого перемножаем тариф на количество для каждой заполненной(базисной) клетки.S= 150*5+100*2+200*1+150*6+50*2+250*1=2150 ден.ед.Приступим к нахождению опорного плана методом «Минимального элемента»Заполнение плана перевозок начнем с ячейки, имеющей минимальную стоимость, а именно, с ячейки G12, в которой тариф (ячейка G7) равен 1. В ячейку G12 поместим максимально допустимую перевозку, равную 300. Поскольку потребность пункта B2 будет удовлетворена, то перевозки в этот пункт от других поставщиков будут равны нулю. Тем самым оказывается заполненным второй столбец. Из оставшихся незаполненных ячеек выбираем новую ячейку с минимальной стоимостью. Пусть это будет I13, у которой тариф равен 1. В ячейку I13 поместим перевозку, равную 250, и тогда в ячейки I11-I12 ставим нулевые перевозки. Заполненным оказывается четвертый столбец. Продолжая этот процесс дальше, получим план перевозок, представленный на рис.2.

---

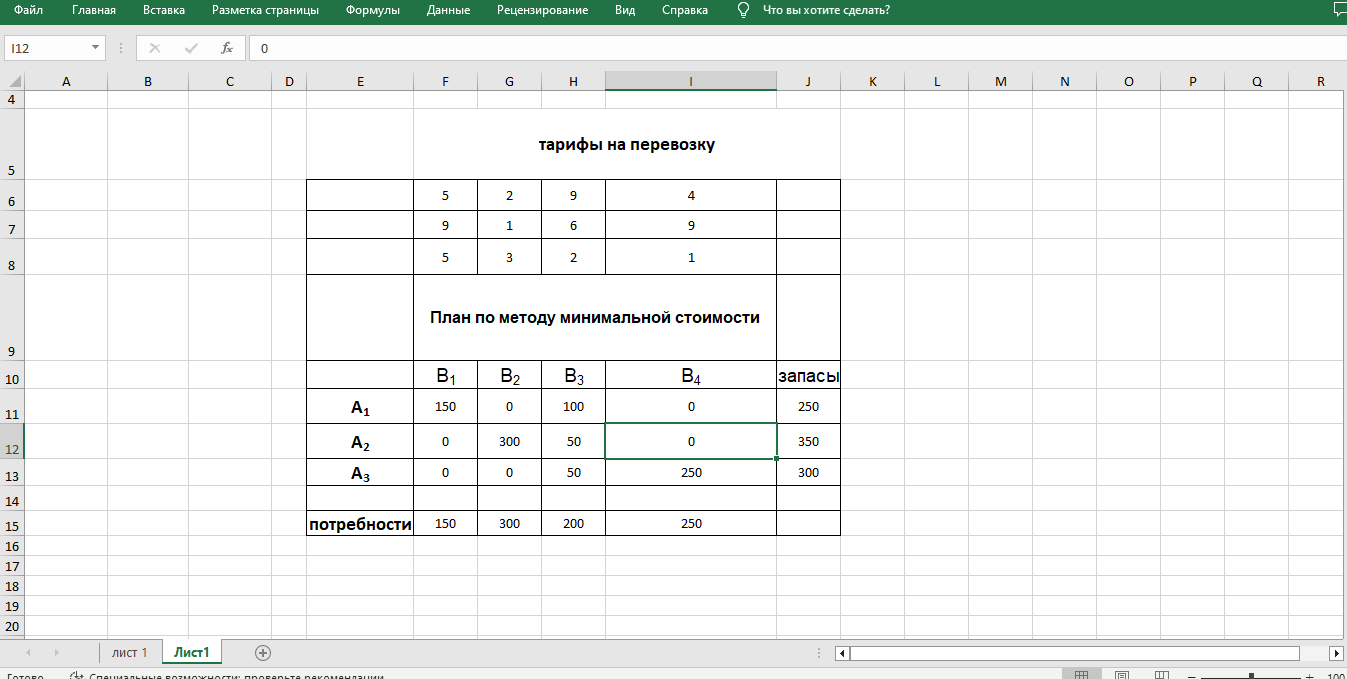
Рис.2 План перевозок по методу «Минимального элемента»Теперь нужно посчитать стоимость начального опорного решения. Для этого перемножаем тариф на количество для каждой заполненной(базисной) клетки.S=5*150+9*100+1*300+6*50+2*50+1*250=2600 ден.ед. Выше были рассмотрены несколько методов для нахождения опорного плана. Теперь необходимо найти оптимальное решение задачи методом потенциалов.Поиск оптимального решения задачи методом потенциалов.В качестве начального опорного решения воспользуемся методом «минимального элемента». Исходные данные возьмем из расчетов выше.1)Подсчитаем число заполненных клеток таблицы перевозок, их 6 и должно быть m+n-1=3+4-1=6. Следовательно, опорный план является невырожденным.2) Найдем потенциалы   по заполненным клеткам перевозок, в которых   (превышение  =0), полагая, что  . 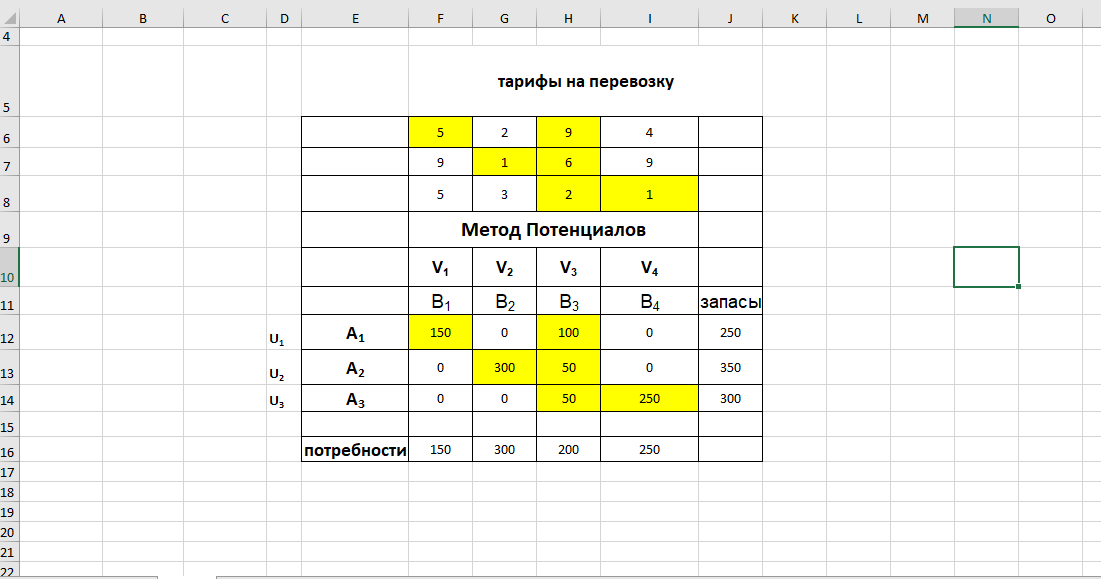Решим систему уравнений:U₁+V₁=5 U₁=0 V₁=5U₁+V₃=9 U₂=-3 V₂=4U₂+V₂=1 U₃=-7 V₃=9U₂+V₃=6 V₄=8U₃+V₃=2U₃+V₄=1Занесем найденные значения потенциалов в таблицу перевозок и вычислим превышения свободных клеток(рис.5):Рис.5 Расчет потенциалов для базисных клеток3) Произведем оценку всех небазисных клеток по формуле: D_ij=C_ij-(U_i+V_j) C₁₂= -2; C₁₄= -4; C₂₁=7; C₂₄=4; C₃₁=3; C₃₂₌6.При оценке не базисных клеток получили несколько отрицательных значений (С₁₂ и С₁₄). Выбираем значение с наибольшим по модулю (С₁₄) и вводим в базис клетку I₁₁. Выполняем построение цикла. 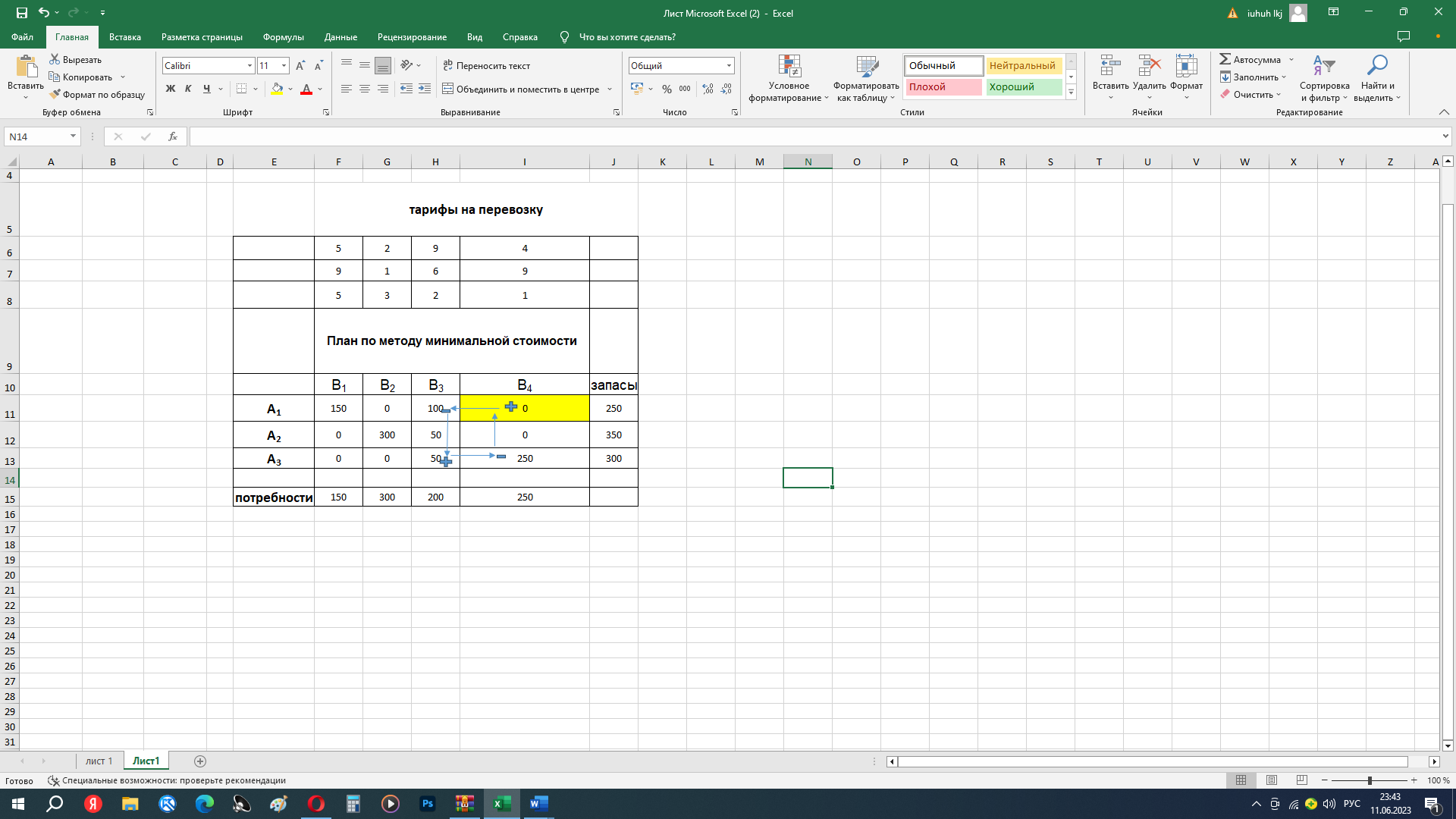(рис.8) Рис.8 Построение циклаВ вершинах цикла, отмеченных знаком «минус», выбираем наименьшее количество перевозок 100.

---

Смотрите также файлы

• 5. получение искусственного холода.pdf

• Конспект занятия Цикл занятий "Учимся дружить. Секреты дружбы".doc

• Исмп это любое клинически распознаваемое инфекционное заболевание, которое поражает больного при поступлении его в стационар или обращение в стационар за лечебной помощью,.pdf

• Задача по взрывобезопасности Вариант задач студенты выбирают по предпо.doc

• Профилактика передачи вичинфекции в работе медицинской сестры.pdf