Практическое задание 2

Рассматривается двухслойный плоский конденсатор, подключенный к источнику напряжения U (см. рис. 1). Заданы пробивные напряженности слоев Е_проб1 и Е_проб2.

Требуется:

• 
  рассчитать напряженность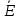 , электрическое смещение 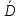, поляризацию 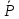для каждого слоя конденсатора;
  
• 
  определить плотность свободных зарядов σна обкладках конденсатора и плотность связанных зарядов σ_связ на границе раздела диэлектриков;
  
• 
  определить электрическую емкость конденсатора на единицу площади;
  
• 
  рассчитать пробивное напряжение U_проб.
  
• 
  построить график распределения потенциала φ вдоль оси x.
  

Ответы привести к размерности: E₁ , E₂ – [кВ/см]; D₁, D₂, P₁, P₂, σ, σ_связ– [пКл/см²];U_проб. – [кB];C – [пФ/см²].

Сделать необходимые выводы.

Таблица 1 – Исходные данные

Первая буква фамилии студента	Вариант	U, кВ	Епроб1, кВ/см	Епроб2, кВ/см	d1, см	d2, см	1	2
С	18	18	29	19	3,3	2,3	1	2

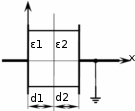
Рис.1. Двухслойный конденсатор

Решение

По условию задания конденсатор заряжен напряжением 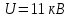. Значит, на обкладках конденсатора имеются заряды противоположных знаков. Разность потенциалов между двумя слоями диэлектриков определяется по формуле: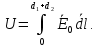



Применительно к скалярным величинам выражение примет вид:



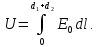
Так как в конденсаторе однородное электрическое поле (

---

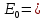const), то для определения разности потенциалов можно использовать формулу: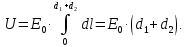


Отсюда:


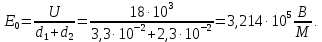
Определим напряженности электрического поля в каждом слое диэлектриков:




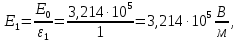
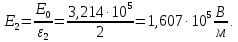
Определим электрическую индукцию в каждом слое диэлектриков:




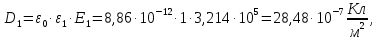
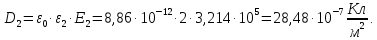
Определим поляризованность каждого слоя диэлектриков:




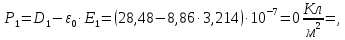
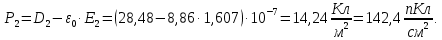
Полученное значение 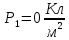указывает на то, что 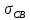(поверхностная плотность свободного заряда на границе раздела диэлектриков) создается только первым диэлектриком: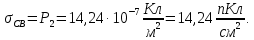


Зависимость напряженности поля внутри конденсатора от плотности свободных зарядов и электрической постоянной выражается формулой:



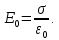
Отсюда:



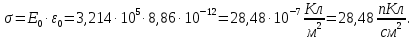
Для определения емкости двухслойного конденсатора представим его в виде схемы последовательного соединения двух однослойных конденсаторов (рис. 2).



Рис. 2. Расчетная схема с двумя конденсаторами
Тогда электрическая емкость каждого конденсатора будет определяться по формуле:


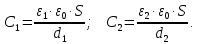
Результирующая емкость последовательно соединенных конденсаторов:


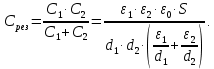
Удельная емкость расчетного двухслойного конденсатора на единицу площади обкладки:

---

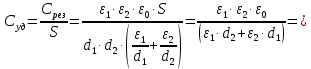
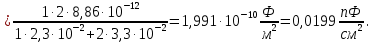
Для случая, когда напряженность примет значение пробивной напряженности, определим её значение для каждого конденсатора в отдельности:






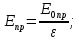
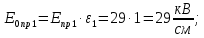
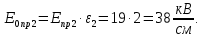
Полученные значения не равны между собой. Далее к расчету принимаем 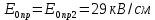. Тогда для определения пробивного напряжения конденсатора воспользуемся формулой (32):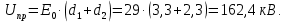


Для того чтобы построить график распределения потенциала 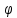вдоль оси 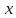, необходимо вычислить электрический потенциал в различных областях конденсатора. Для вычисления потенциала необходимо составить уравнения. Связь между электрическим потенциалом и напряженностью электрического поля отражается в формулой: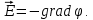


По заданию потенциал изменяется только вдоль оси х, поэтому применим уравнение (34):


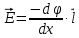
В случае если потенциал между обкладками конденсатора изменяется только вдоль оси х, вектор напряженности сонаправлен с осью 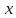, поэтому можно перейти от векторных единиц к их модулям: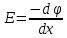



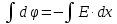
Так как электрическое поле между обкладками конденсатора является однородным (по заданию), то изменение потенциала соответствует формуле:



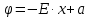
где а – постоянная интегрирования.
Для первого диэлектрика:

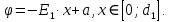(1)
Для формулы (1) определим постоянную интегрирования :

---

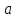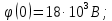
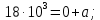
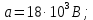
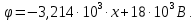
Для второго диэлектрика:

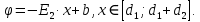(2)
Для формулы (2) определим постоянную интегрирования :








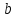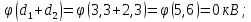
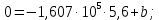
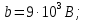
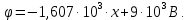
Определим электрический потенциал для различного расстояния относительно ширины первого и второго диэлектриков 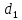и .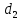

Для области первого диэлектрика:

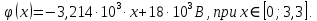(3)
Для области второго диэлектрика:

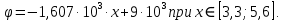(4)
По формулам (3) и (4) построим график зависимости 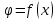для обеих обкладок конденсатора в одной координатной сетке (табл. 2, рис. 3).
Таблица 2 – Данные для построения зависимости 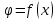двухслойного конденсатора

	Первый слой			Второй слой
, см	0	1,3	3,3		3,3	4,4	5,6
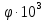,В	18	13,821	7,393		3,696	1,929	0

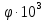, В

---

, см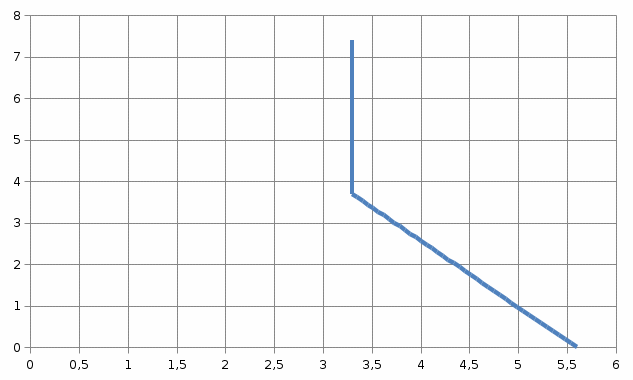


Рис. 3. Зависимости двухслойного конденсатора
Вывод: электрический потенциал имеет скачкообразное изменение на границе раздела слоев.

---

Смотрите также файлы

• Российский и международный подход к управлению.pdf

• Технологические измерения и приборы.docx

• Отчет по профессиональной и производственной практике Студент Еркенова Бакытгуль Бериковна Курс 3 группа пдр32.docx

• Задание на учебную практику Исходные данные.docx

• Решение Ситуация 1 при гашении расчетноплатежных ведомостей вместо даты оплаты указывалась только сумма, оплаченная по ведомости.docx