Программирование в САПРЛабораторная работа №2Тема занятия:Численные методы. Нахождение определенных интегралов.Аннотация:Изучение численных методов нахождения значений определенных интегралов.План занятия:

1. 
   Подготовка к выполнению работы, в том числе:
   
   1. 
      изучение теоретических основ численных методов нахождения значения определенных интегралов;
      
   2. 
      повторение ранее изученного материала по архитектуре MFC DialogBased Application;
      
2. 
   Создание диалогового приложения на языке C++ для нахождения значения определенного интеграла тремя методами в соответствии с индивидуальным заданием.
   
3. 
   Защита лабораторной работы.
   

При решении практических инженерных задач часто возникает необходимость нахождения значений определенных интегралов, причем в ряде случаев аналитическое решение данной задачи представляется весьма затруднительным. На помощь в этой ситуации приходят численные (приближенные) методы решения.Суть численных методов нахождения значений определенных интегралов вытекает из геометрического смысла определенного интеграла. Из математики известно, что значение определенного интеграла равно площади криволинейной трапеции ограниченной графиком подынтегральной функции, пределами интегрирования и осью абсцисс. То есть для упрощенного численного решения достаточно каким-либо образом вычислить эту площадь. Для нахождения искомой площади мы рассмотрим 3 метода: прямоугольников, трапеций и парабол (Симпсона).Метод прямоугольников состоит в разбиении искомой площади на прямоугольные интервалы малой величины, в пределах которых подынтегральная функция может быть заменена (аппроксимирована) горизонтальной линией, причем в зависимости от того какая точка интервала разбиения принимается за «базу» для горизонтальной линии мы получаем методы левых, средних и правых прямоугольников (рисунок 1).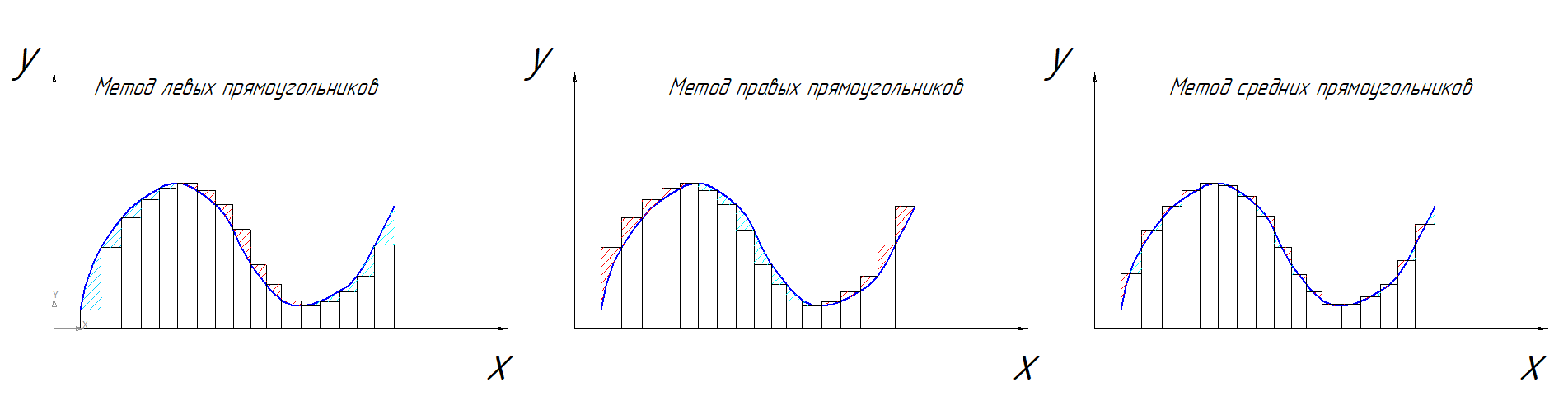Рисунок 1. Методы левых, средних и правых прямоугольниковРасчет площади производят в соответствии со следующими формулами:Метод левых прямоугольников

---

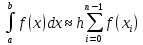
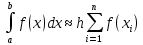
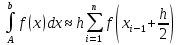
: Метод правых прямоугольников: Метод средних прямоугольников: В приведенных выше формулах h – ширина интервала разбиения (шаг по оси Х).Развитием метода прямоугольников является метод трапеций (рисунок 2). Отличие заключается в том, что подынтегральная функция на каждом участке разбиения заменяется уже не горизонтальной, а наклонной прямой. В результате получается трапеция, площадь которой вычисляется по известной зависимости как произведение полусуммы длин оснований (значений функции на краях интервала) на высоту (ширину разбиения). 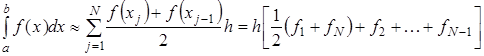Расчетная формула в этом случае будет выглядеть следующим образом (формула 1).Формула 1. 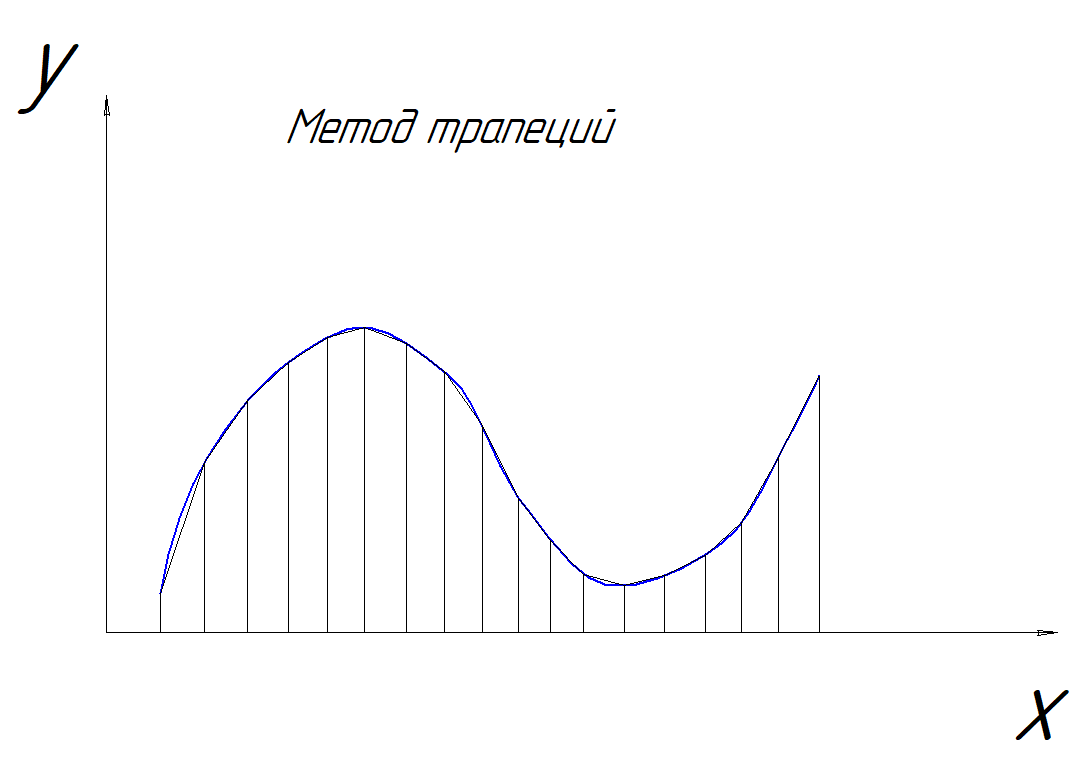Расчетная формулаРисунок 2. Метод трапеций Суть метода Симпсона заключается в замене подынтегральной функции квадратным полиномом (параболой). При этом в расчете одновременно участвуют два соседних интервала разбиения, так как парабола однозначно определяется тремя точками. Метод парабол считается наиболее предпочтительным для вычисления определенного интеграла из перечисленных. 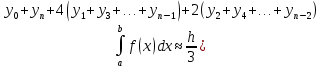Расчетная формула метода парабол выглядит следующим образом (формула 2).Формула 2. Расчетная формула метода параболОчевидно, что, исходя из специфики метода Симпсона, число разбиений участка интегрирования N должно быть четным.Задание для самостоятельной работыРазработать MFC Dialog Based Application для сравнения методов численного интегрирования: прямоугольников, трапеций и парабол. Предусмотреть ввод пределов интегрирования, вывод результата и выбор метода расчета. Подынтегральное выражение и пределы интегрирования для тестирования приложения взять из нижеследующей таблицы в соответствии с вариантом задания. Предусмотреть в приложении функционал оценки точности интегрирования различными рассматриваемыми методами и определить для своего варианта задание критическое число N – разбиений при котором относительная погрешность каждого из методов станет более 1% (таблица 1).

---

Таблица 1. Задания для самостоятельной работы

№ варианта	а	b	f(x)
1	0,6	1,5
2	1,2	2,832
3	1,3	2,956
4	2,8	4,408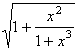
5	0,8	2,528
6	-0,52	1,58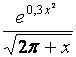
7	0,2	2,12
8	1,5	3,42
9	1,1	2,876
10	0,31	1,93
11	1,5	3,18
12	-1,3	0,476
13	1,0	2,76
14	2,4	4,08
15	1,82	3,464
16	1,5	3,24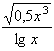
17	1,4	3,008
18	-0,2	1,252
19	0,15	1,878
20	-0,52	1,58
21	0,3	1,844
22	3,5	4,94
23	0	1,44
24	5,1	6,54
25	1,42	2,98
26	1,2	2
27	1,6	2,4
28	0,2	1
29	0,6	1,4
30	0,4	1,2

---

 Форма представления выполненного заданияНа проверку преподавателю требуется представить архив (RAR, ZIP) с проектом MS Visual Studio, реализующим задание для самостоятельной работы.

---

Смотрите также файлы

• Контрольные вопросы 3 Сформулируете формулу Бернулли. Ответ.docx

• Отчет о практике Название дисциплины Производственная практика, по получению профессиональных умений и опыта профессиональной деятельности, правоохранительная бакалавриат 40. 03. 01 Юриспруденция, уголовноправовая.doc

• Разработка программного обеспечения и его применение в авиационнокосмической промышленности Аннотация.docx

• Выделяют следующие методы организации управленческого учета Нормативный метод Стандарткост.docx

• Волгоград 2019 г.docx