Файл: Лабораторная работа 1 анализ частотных и временных характеристик пассивного и активного четырехполюсников.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 109
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ
Дисциплина: Теория электрических цепей
Лабораторная работа 1
АНАЛИЗ ЧАСТОТНЫХ И ВРЕМЕННЫХ ХАРАКТЕРИСТИК
ПАССИВНОГО И АКТИВНОГО ЧЕТЫРЕХПОЛЮСНИКОВ
с использованием программы FASTMEAN
Вариант 3
Фамилия:___Чудинов____
Имя:___Кирилл____
Отчество:_Витальевич__
Группа №:____РБ-11з______
Проверил:______________
Санкт-Петербург
2023
1.Цель работы
1.1. Исследовать частотные характеристики пассивного четырехполюсника: амплитудно-частотную│H(jω)│ и фазо-частотную θ(ω).
1.2. Исследовать временные характеристики пассивного четырехполюсника: переходную характеристику h(t) и импульсную g(t).
1.3. Оценить связь между временными и частотными характеристиками исследуемого четырехполюсника.
2.Задание на самостоятельную подготовку к работе
2.1. Изучите теоретические вопросы, связанные с нахождением операторных передаточных функций и частотных характеристик пассивных и активных четырехполюсников.
2.2. Изучите теоретические вопросы, связанные с нахождением временных характеристик по известной операторной передаточной функции.
2.3. Найдите операторную передаточную функцию H(p)=U2(p)/U1(p) пассивного четырехполюсника 3-го порядка, соответствующего вашему номеру варианта, схема и параметры которого даны в табл. 5.1.
Таблица 5.1 - Схемы пассивных четырехполюсников
| Вариант | Схема пассивной цепи | Параметры |
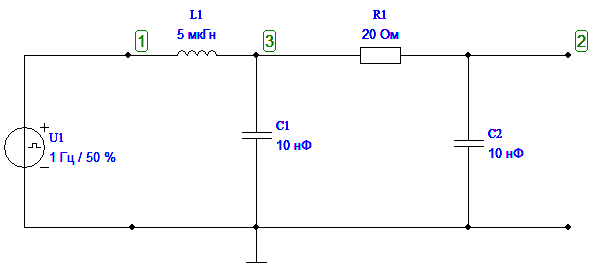
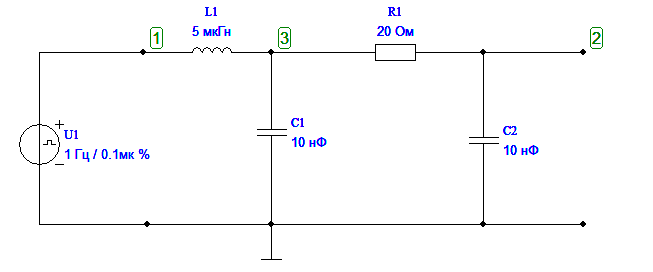
| 3 | 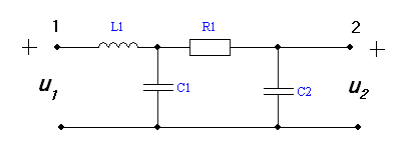 | L1=5 мкГн C1= С2=10 нФ R1=20 Ом |
3. Задание для работы в компьютерном классе
3.1. Загрузите программу FASTMEAN. Описание работы с программой приведено в приложении методических указаний.
3.2. Постройте на экране дисплея схему пассивной цепи, выбрав ее из табл. 5.1 в соответствии со своим номером варианта.
3.3. Подключите к входным зажимам цепи источник напряжения. На вкладке «Параметры» задайте «Тип источника» - «Гармонический», сделав выбор в раскрывающемся списке.
3.4. Заземлите базисный узел. Пронумеруйте узлы, нажав кнопку «Показать номера узлов» на панели инструментов.
3.5. Постройте и зарисуйте частотные характеристики цепи АЧХ и ФЧХ в линейном масштабе. Для этого на панели инструментов выберите кнопку «Анализ» → «АЧХ/ФЧХ». Начальную частоту выберите равной 1 Гц, конечную частоту - 10 МГц. Указанные значения в дальнейшем следует откорректировать так, чтобы на экране дисплея достаточно хорошо отображались основные особенности АЧХ и ФЧХ исследуемой цепи. Выберите число точек для расчета, равное 1000.
3.6. Определите по графику АЧХ с помощью линейки полосу пропускания цепи на уровне Hmax/√2 , где Hmax =max │Н (jω)│.
3.7. Определите по графику АЧХ граничные значения амплитудно-частотной характеристики:
lim│Н (jω)│= │Н (0)│; lim│Н (jω)│= │Н (∞)│.
ω→0 ω→∞
3.8. Смоделируйте на входе цепи единичное ступенчатое воздействие 1(t). Задайте параметры источника:
«Тип источника» – меандр
«Частота (f)» – 1 Гц
«Коэффициент заполнения (К)» – 50%
«Макс.напряжение (Umax)» – 1 В
«Мин.напряжение (Umin)» – 0 В
«Длительность фронта (tfr)» – 1 нс
«Задержка включение (delay)» – 0 пер
3.9. Постройте и зарисуйте переходную характеристику цепи h(t). Рекомендуемые параметры в таблице анализа:
«Начальное время» - 0
«Конечное время» - 5 мкс
«Число точек» – 10000
Определите по графику с помощью линейки предельные значения h(t):
lim h(t)= h(0); lim h(t)= h(∞).
t→0 t→∞
3.10. Смоделируйте на входе единичное импульсное воздействие δ(t). Задайте параметры источника:
«Тип источника» – меандр
«Частота (f)» – 1 Гц
«Коэффициент заполнения (К)» – 0,1мк %
«Макс.напряжение (Umax)» – 10Г В
«Мин.напряжение (Umin)» – 0 В
«Длительность фронта (tfr)» – 1 нс
«Задержка включение (delay)» – 0 пер
3.11. Постройте и зарисуйте импульсную характеристику цепи g(t). Рекомендуемые параметры в таблице анализа:
«Начальное время» - 0
«Конечное время» - 5 мкс
«Число точек» – 10000
3.12. Получите выражение изображения для операторной передаточной функции четырехполюсника. Для этого на панели инструментов выберите кнопку «Анализ» → «Символьный». В появившемся диалоговом окне выберите величину, соответствующую выходному напряжению четырехполюсника. Включите опцию «Показать все формулы» и нажмите кнопку «Получить». Скопируйте получившееся выражение операторной передаточной функции. Сравните полученное выражение с предварительно рассчитанным H(p)=U2(p)/U1(p) .
4. Указания защите
4.1. Отчет должен содержать:
- схемы исследуемых цепей;
- вывод аналитических выражений для операторных передаточных функций пассивного четырехполюсника 3-го порядка и ARC-фильтра 2-го порядка;
- графики частотных характеристик АЧХ и ФЧХ, рассчитанных на ПК для каждой цепи, с указанием на графиках АЧХ полосы пропускания;
- графики переходных h(t) и импульсных g(t) характеристик, рассчитанных на ПК для каждой цепи;
- проверьте выполнение соотношений между предельными значениями переходных характеристик цепей (при t=0 и t→∞) и их АЧХ (при ω=0 и ω→∞):
lim h(t)= h(0)=H(∞); lim h(t)= h(∞)=H(0).
t→0 t→∞
- определите количество и характер полюсов H(p) по виду H(p) и графикам переходных характеристик пассивной и активной цепей и качественно покажите их на комплексной плоскости.
4.2. Подготовьтесь к ответу на контрольные вопросы.
Отчет:
1)
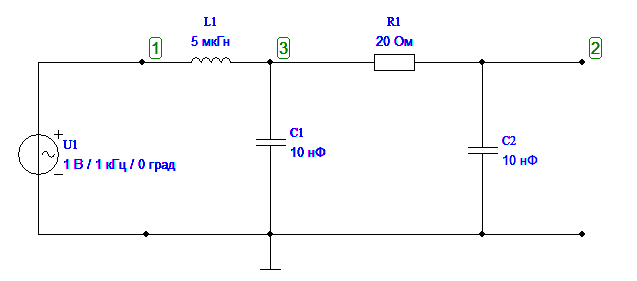



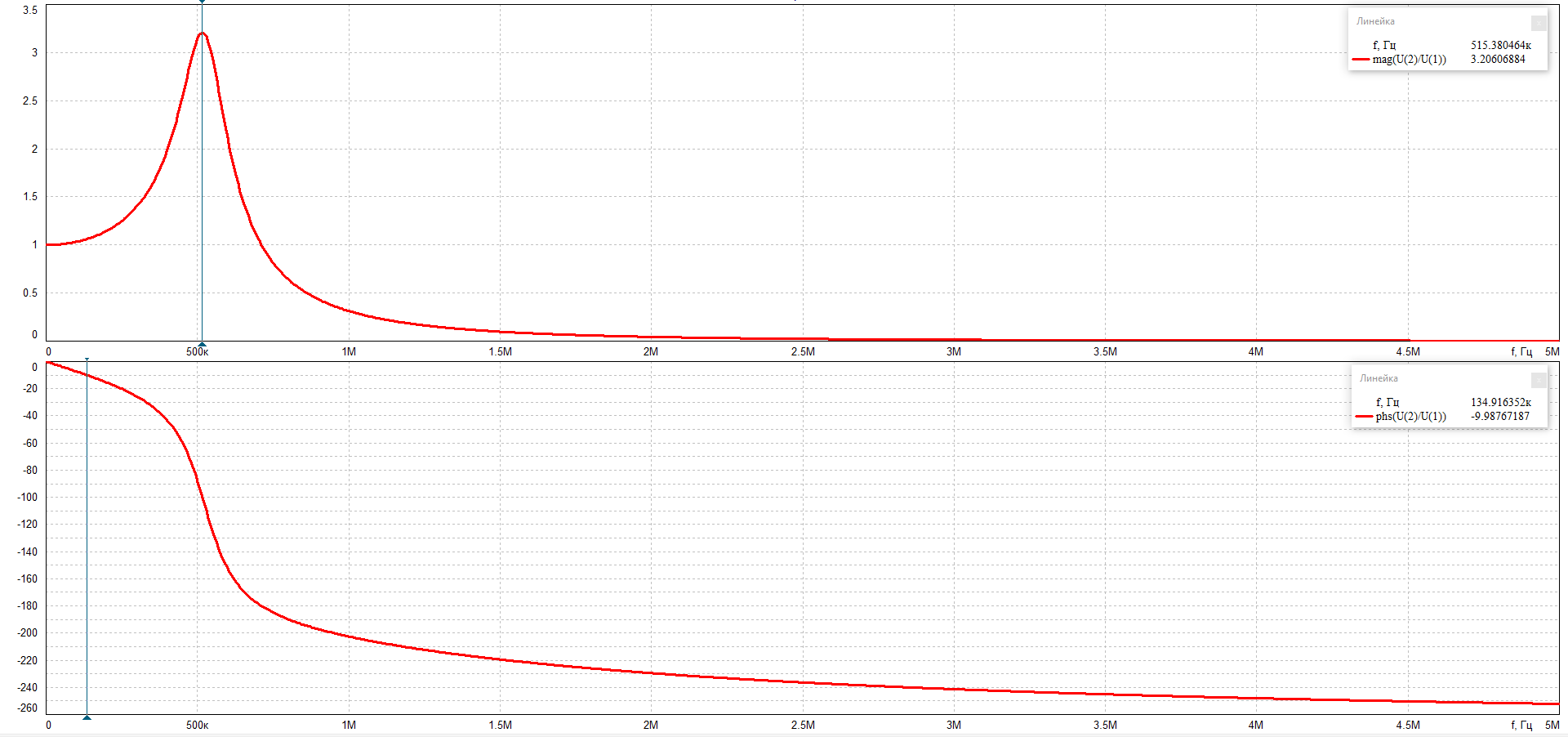
Полоса пропускания получилась от 426 кГц до 591 кГц и составляет 165кГц.
Граничные значения равны:
lim│Н (jω)│= │Н (0)│=1;
ω→0
lim│Н (jω)│= │Н (∞)│=0.
ω→∞
Запишем узловые уравнения для узлов 2 и 3:
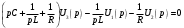
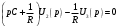
Из второго уравнения выражаем U3(p) через U2(p):
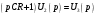
и подставляя в первое уравнение, получаем:
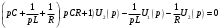
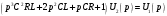
Тогда отношение U2(p)/U1(p) примет вид:
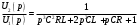
а операторная передаточная функция:
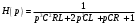
2)
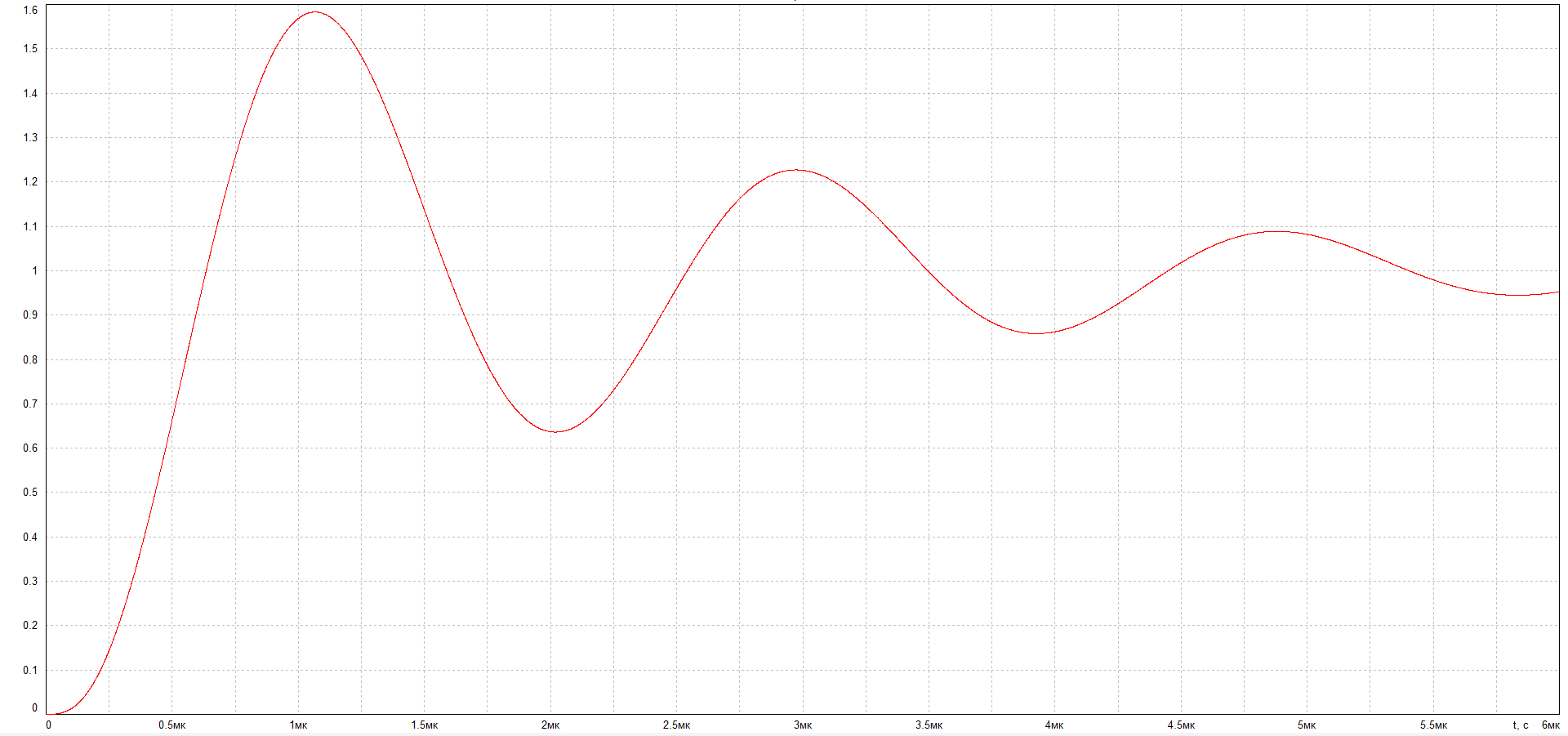
lim h(t)= h(0)=0;
t→0
lim h(t)= h(∞)=1.
t→∞
3)
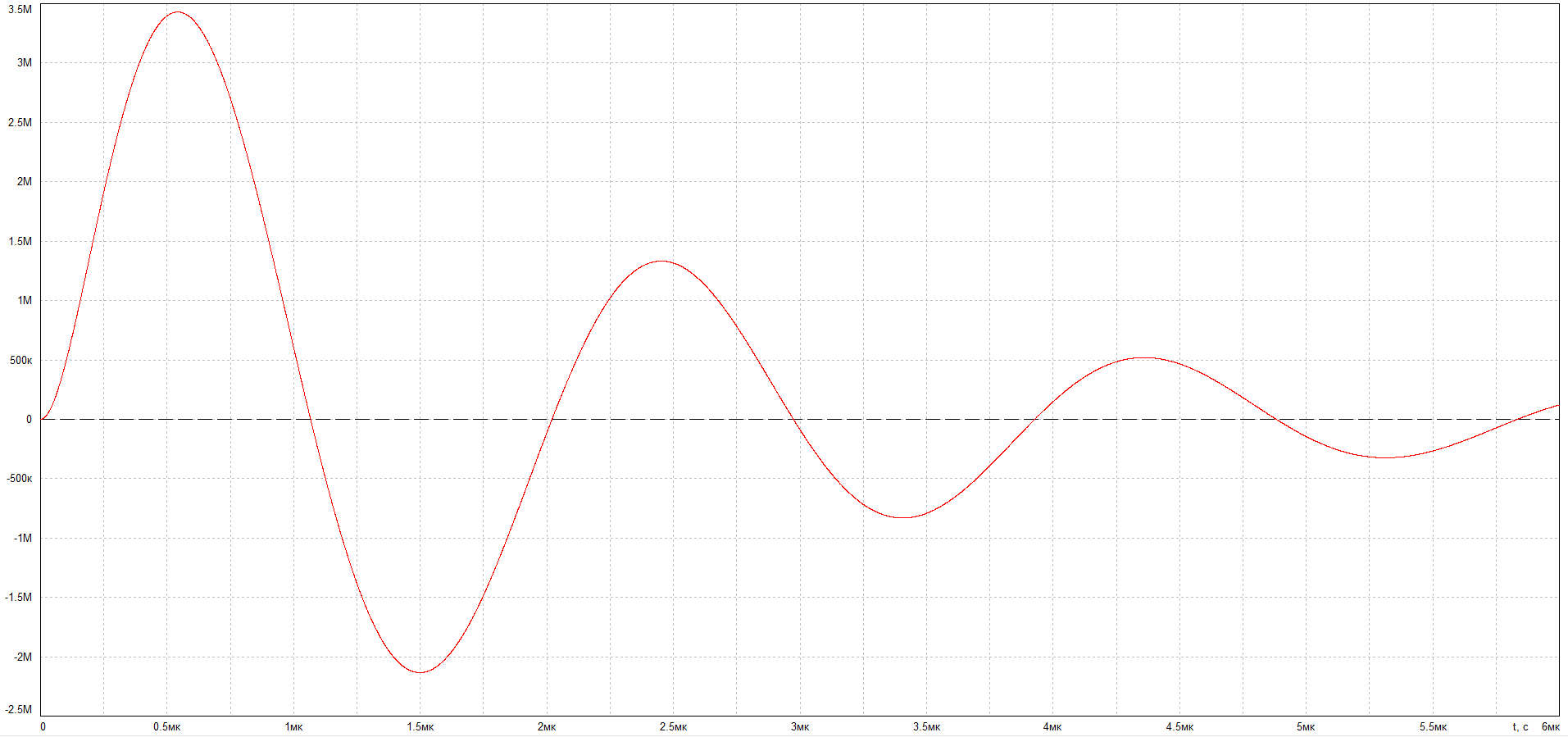
4) Получим выражение изображения для операторной передаточной функции четырехполюсника.
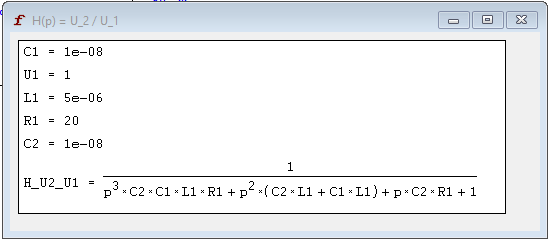
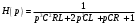
Вывод: выражения передаточной характеристики, полученные с помощью FASTMEAN, совпадают с расчетным выражением.