1.8Вероятность безотказной работы гироскопа в течение t =150 часравна 0,9. Время исправной работы подчинено закону Вейбулла с парамет­ром α = 2,6. Необходимо определить интенсивность отказов, частоту отказов гироскопов для t =150 час и среднюю наработку до первого отказа. РешениеЗначение гамма-функции Г(1,38) = 0,888542.8Система состоит из трех устройств. Вероятности безотказной работы каждого из них в течение времени t =100 час равны: p 1 (100) =0,95; р 2 (100) =0,96 p 3 (100) =0,97. Справедлив экспоненциальный закон надежности. Необходимо найти среднюю наработку до первого отказа системы.Решение. Найдем вероятность безотказной работы изделия: Р С (100) =p 1 (100)р 2 (100) p 3 (100) =0,95*0,96*0,97 = 0,92.Найдем интенсивность отказов изделия, воспользовавшись формулойимеем или  1/час.ТогдаT cp c =  часАвтомобильный двигатель имеет l=4 свечи зажигания по одной на каждый цилиндр. Интенсивность отказов свечи =10^3 1/час, а длительность работы двигателя в течение всего путешествия t=20 час. Предполагается, что автомобиль может ехать также при одном неработающем цилиндре. Необходимо определить вероятность безотказной работы двигателя P_c(t), среднее время безотказной работы двигателя m_tc , частоту отказов f_c(t), интенсивность отказов _c(t) двигателя. Какова вероятность того, что автомобиль доставит туристов в пункт назначения без замены свечей?
Решeниe.Найдем вероятность безотказной работы устройства 

---

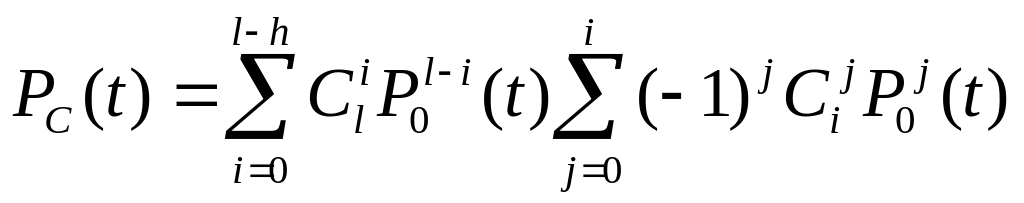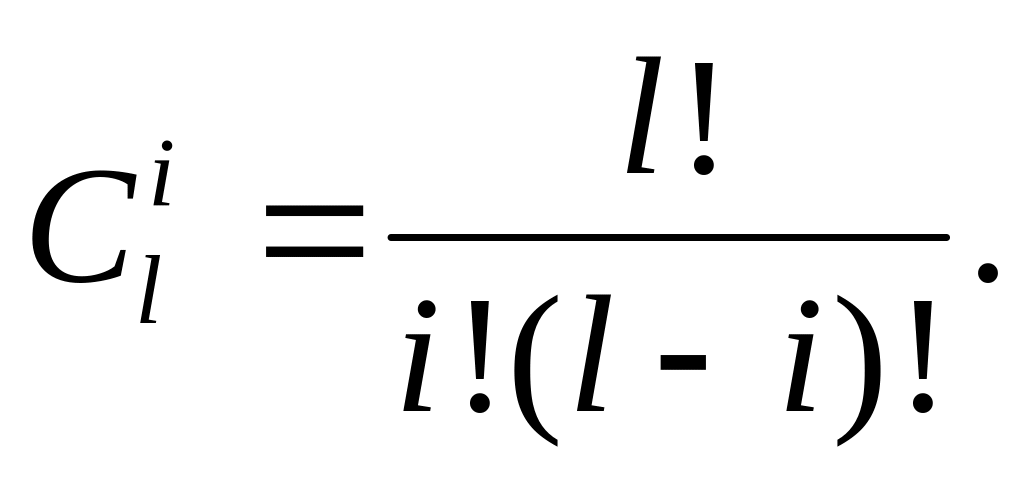
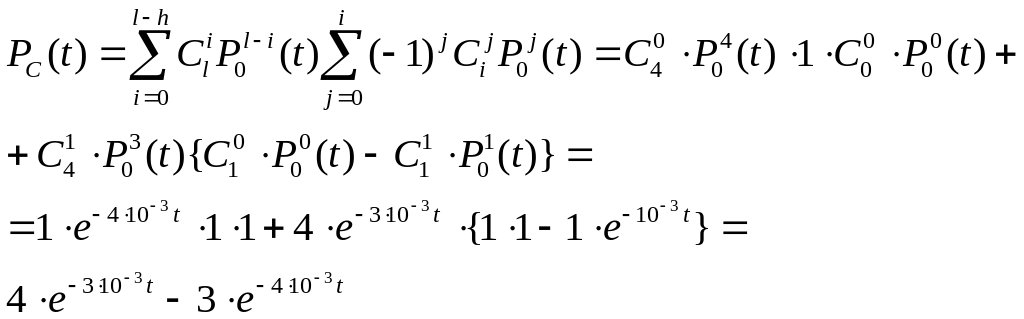
P_c (t) :  ,гдеР_о(t) - вероятность безотказной работы основной системы или любой резервной системы; l - общее число основных и резервных систем; h  число систем, необходимых для нормальной работы.Из условия задачи:l = 4h = 3Тогда        Будем предполагать, что для любой отдельно взятой системы справедлив экспоненциальный закон надежности, т.е.ТогдаДля данных нашей задачи   t =   *20=0,02.ТогдаP_c(20)=   .Среднее время безотказной работы будет: 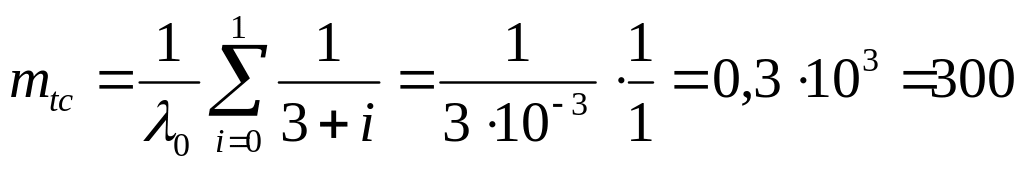   час.Определим частоту отказов f_c(t). Имеем  (20)= 

---

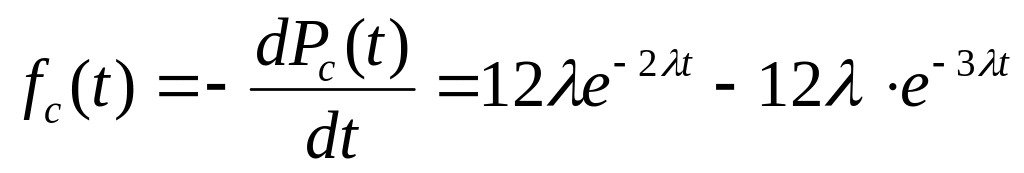
 (1/час)

Определим интенсивность отказов _с(t). Получим

 .

---

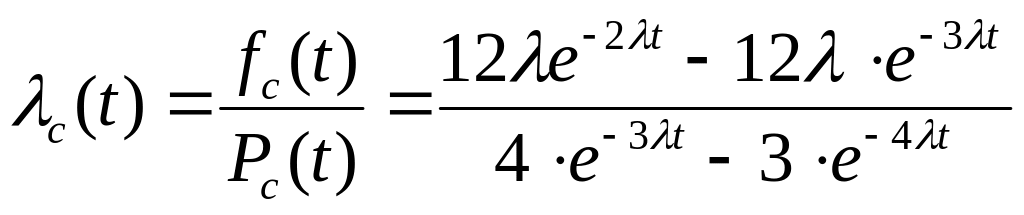Смотрите также файлы

• Презумпция невиновности как принцип уголовного судопроизводства.rtf

• Введение в права человека Кафедра международного права и прав человека тгюу план.pptx

• "чистота", так как в предложении используется неаккуратное сочетание слов "финансовое резюме деятельности предприятия", которое не является стандартным выражением в русском языке..docx

• Задачи Методом изоклин построить интегральные кривые уравнения.docx

• Кафедра конструкторско технологическое обеспечение машиностроительных производств 15. 03.docx