Задача 1. Рассчитать наибольшее и наименьшее значения функции на заданном отрезке:



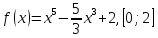
Решение.

Находим первую производную функции:



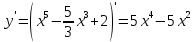
Приравниваем ее к нулю:













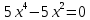
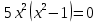
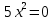
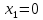
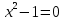
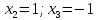
Третий корень во внимание не берем, так как он не входит в указанный отрезок.

Вычисляем значения функции на концах отрезка













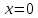
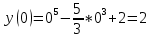
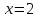
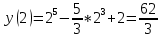
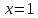
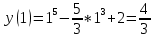
Ответ:




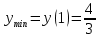
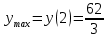
Задача 2. Провести полное исследование и построить графики данных функций:





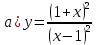
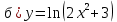
Решение.



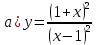
1) Найти область определения функции, исследовать её поведение на границах этой области:

Область определения функции 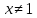, то есть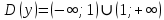

2) Найти точки разрыва и классифицировать их с помощью односторонних пределов:

---

Точка разрыва .

Вычислим односторонние пределы:





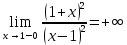
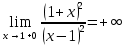
является точкой разрыва второго рода

3) Исследовать периодичность, чётность (нечётность):

Функция ни чётная, ни нечётная. Симметрии относительно оси ординат нет. Симметрии относительно начала координат тоже нет. Так как 



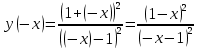
Видим, что  



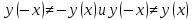
4) Найти точки пересечения графика с осями координат и интервалы знакопостоянства функции:

Точки пересечения с осями координат:





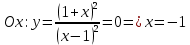
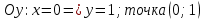
5) Найти асимптоты:

Вычислим односторонние пределы:





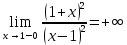
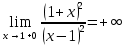
Получаем, что 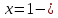вертикальная асимптота

Наклонные асимптоты вида





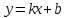
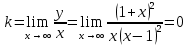
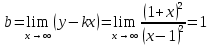
Наклонная асимптота

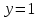
6) Найти точки экстремума и интервалы монотонности:

Вычисляем первую производную



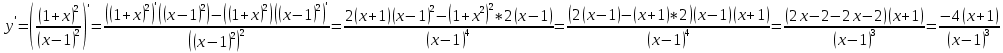
Находим критические точки, т.е. приравниваем производную к нулю:



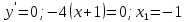
Исследуем знак производной на интервале, на котором критические точки делят область определения функции.


Функция убывает на интервале 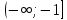и возрастает на интервале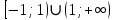

---

. Функция имеет минимум в точке





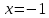
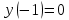
7) Найти точки перегиба и интервалы выпуклости и вогнутости:

Вычисляем вторую производную



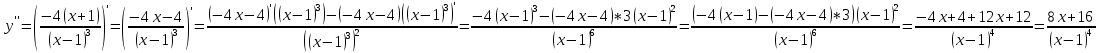
Находим критические точки, т.е. приравниваем вторую производную к нулю:



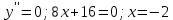
Исследуем знак производной на интервале, на которые критическая точка делит область определения функции:


Функция выпукла вверх на интервале 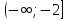, выпукла вниз на интервале .

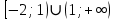Точка перегиба:





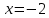
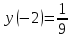
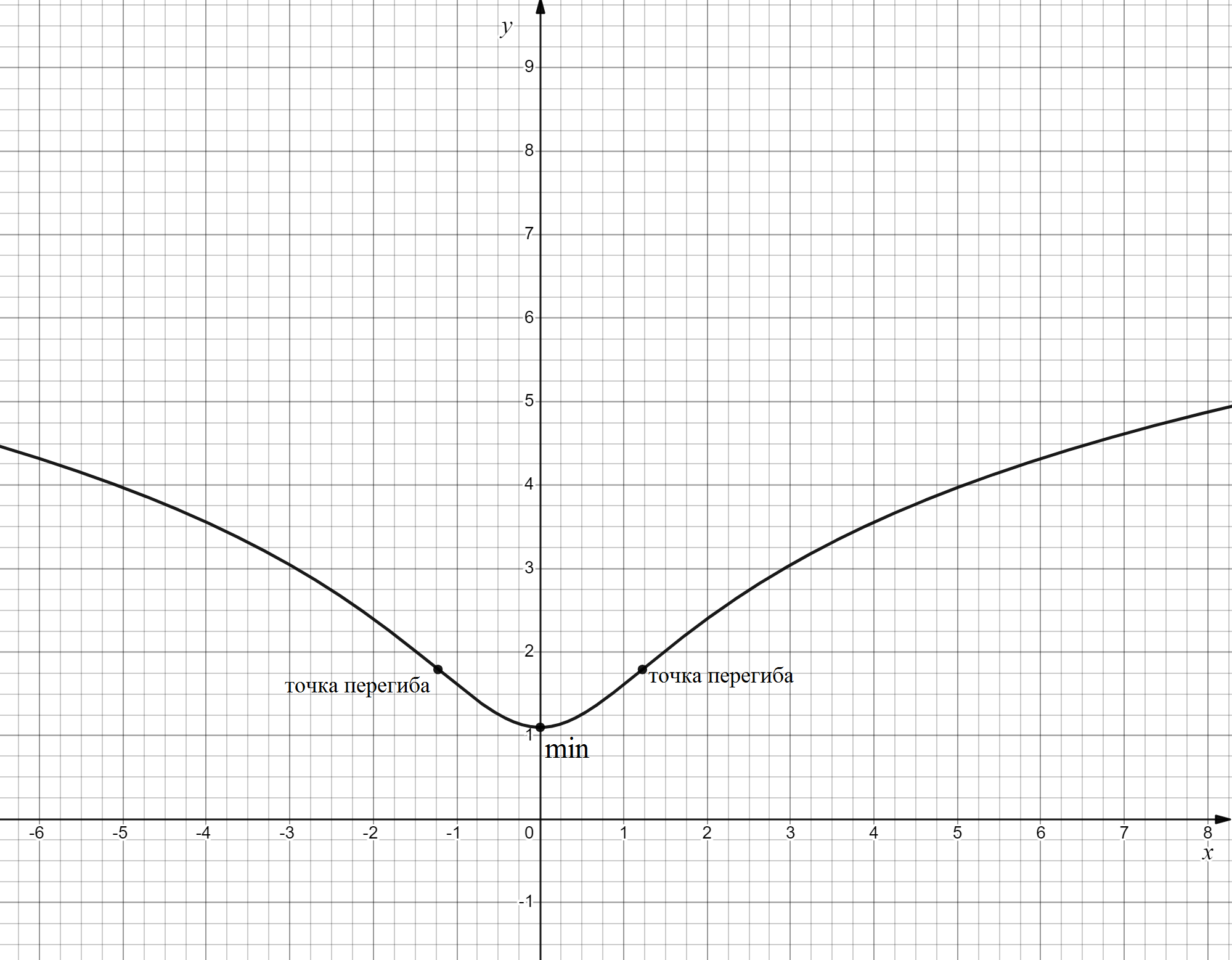
8) Построить график, используя полученные результаты




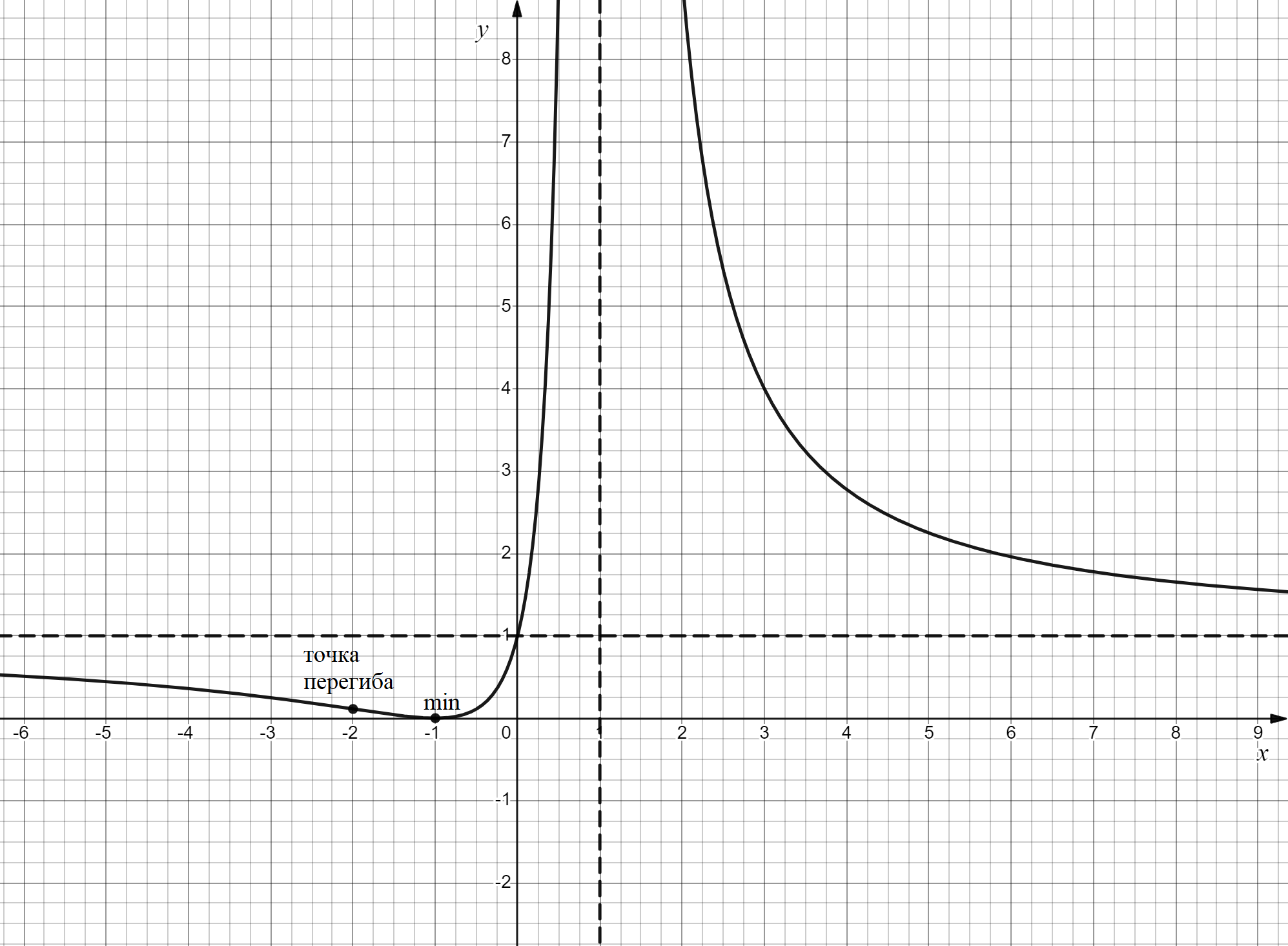
1) Найти область определения функции, исследовать её поведение на границах этой области:

Область определения функции 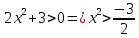, то есть .

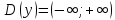Область значений функции

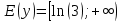
2) Найти точки разрыва и классифицировать их с помощью односторонних пределов:

Точек разрыва нет.

3) Исследовать периодичность, чётность (нечётность):

Функция является четной. Так как 



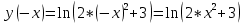
Видим, что  



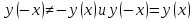
4) Найти точки пересечения графика с осями координат и интервалы знакопостоянства функции:

---

Точки пересечения с осями координат:





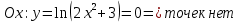
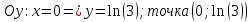
5) Найти асимптоты:

вертикальных асимптот нет

Наклонные асимптоты вида





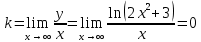
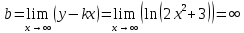
Наклонных асимптот нет.

6) Найти точки экстремума и интервалы монотонности:

Вычисляем первую производную



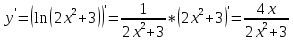
Находим критические точки, т.е. приравниваем производную к нулю:



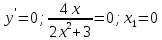
Исследуем знак производной на интервале, на котором критические точки делят область определения функции.



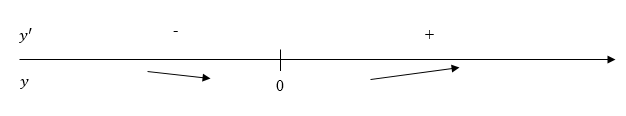
Функция убывает на интервале 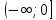и возрастает на интервале 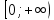. Функция имеет минимум в точке





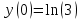
7) Найти точки перегиба и интервалы выпуклости и вогнутости:

Вычисляем вторую производную



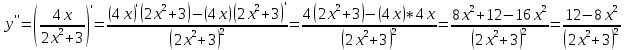
Находим критические точки, т.е. приравниваем вторую производную к нулю:



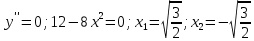
Исследуем знак производной на интервале, на которые критическая точка делит область определения функции:



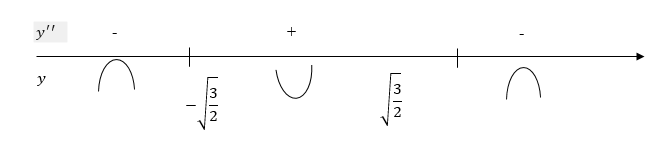
Функция выпукла вверх на интервале 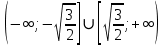, выпукла вниз на интервале 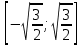. Точка перегиба: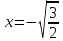

---

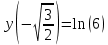
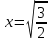
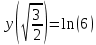
8) Построить график, используя полученные результаты

---

Смотрите также файлы

• Отчет о практике Педагогическая практика была пройдена в доу 15, г. Нижний Новгород.docx

• Дисциплина Математика Практическое занятие 2 Обучающийся Баранова Кристина Евгеньевна Преподаватель Сазонова Элеонора Борисовна.rtf

• Здоровый образ жизни Работу выполнил студент 12 группы Разуваев Ярослав.pptx

• Государственные деятели.docx

• Проводники.docx