Задача Д1

4.1. Условия задачи. Барабан радиусом R и весом Р (рис.4.1), имеющий выточку радиусом r = 0,6 Rс намотанным на нее тросом, находится в зацеплении с наклонной плоскостью (может катиться по плоскости без проскальзывания). Угол между наклонной плоскостью и горизонталью . Радиус инерции барабана с тросом  = 0,5 R.

На барабан помимо силы веса 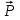действуют следующие активные (заданные) нагрузки:

 сила натяжения троса 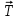, действующая по касательной к выточке, точка её приложения задается углом , отсчитываемым от нормали к плоскости, как показано на рис. 4.1;

 горизонтальная сила 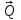, приложена к оси С барабана;

 пара сил с моментом М.

Численные значения характеристик плоскости, барабана и заданных нагрузок для различных вариантов задачи приведены в табл. Д 1.

Под действием указанных сил барабан начинает движение из состояния покоя.


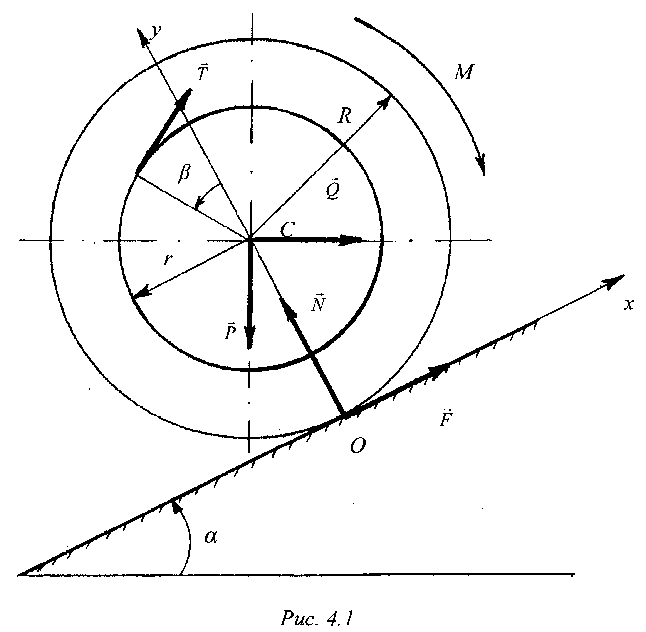
Таблица Д1

Исходные данные к задаче Д1

№ строки	R, м	Р, кН		, град	, град	Q, кН	М, кНм	Т, кН
7	0,8	12		15	 90	4	4	 1
8	0,9	8		 15	 60	 4	 6	4
9	1,0	10		30	 45	2	 4	3
0	1,2	12		 30	 30	 2	 6	4
	По первой цифре шифра		По второй цифре шифра				По третьей цифре шифра

---

Определим ускорение центра масс барабана с помощью уравнений плоскопараллельного движения твердого тела. Применительно к рассматриваемой расчетной схеме (рис.1.1) они принимают вид:







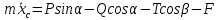
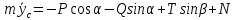
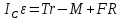
Вычислим предварительно ряд характеристик барабана, входящих в уравнения движения и, следовательно, необходимых для дальнейших расчетов:










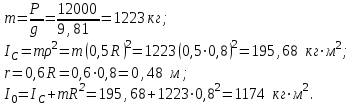
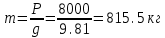
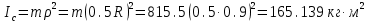
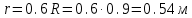
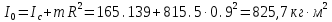
Исключим из уравнения (в) неизвестное угловое ускорение , заменив его эквивалентной величиной 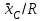(см. выражение (4.2)). Одновременно разделим это уравнение на постоянное число R: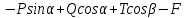



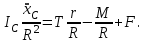(г)

Такая запись уравнения (в) позволяет сравнительно просто исключить из уравнений движения неизвестную силу 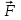за счет почленного сложения уравнений (а) и (г).

ускорение центра масс барабана:


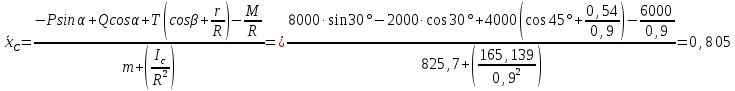
Вычислим также величину силы F , которая необходима для обеспечения качения барабана без проскальзывания. Из уравнения (а) следует, что





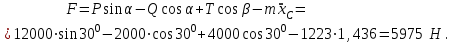
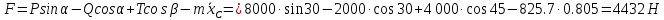
Для определения закона движения центра масс барабана служит полученное дифференциальное уравнение:

.

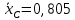Интегрируя данное выражение, получаем:

;

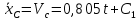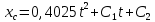
Закон движения центра масс барабана:

---

;

.

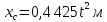
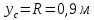Найдем значение вторым способом. Для этого составим уравнение вращательного движения барабана вокруг оси, проходящей через точку контакта барабана и плоскости – через точку О:





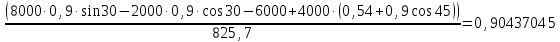
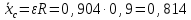
Задача СМ1
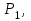
Условие задачи. Для стального стержня заданной длины (рис.1.1) и нагруженного тремя осевыми силам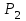и и 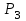необходимо:

– построить эпюру продольных сил N;

– при допускаемых напряжениях на растяжение 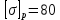и на сжатие 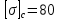МПа подобрать постоянное по длине поперечное сечение;

– построить эпюру нормальных напряжений 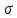по длине бруса;

– построить эпюру продольных перемещений сечений бруса, приняв модуль упругости материала Е = 2·10⁵ МПа;

– вычислить работу внешних сил и потенциальную энергию деформации бруса.

Необходимые исходные данные взять из табл. 1.1.

Методические рекомендации. Для построения эпюры продольных сил использовать метод сечений. Из этого метода следует, что продольная сила в рассматриваемом сечении численно равна алгебраической сумме всех сил, расположенных по одну сторону от сечения. При суммировании силу необходимо считать положительной, если она растягивает стержень (направлена от сечения), и отрицательной – если сжимает (направлена к сечению).

Так как допускаемые напряжения на растяжение и на сжатие неодинаковы, площадь поперечного сечения определяется как для растянутых, так и для сжатых участков. В качестве расчетной выбирается большее из полученных значений.
Таблица 1.1

Исходные данные к задаче СМ1

---

№ cтроки	Схема на рис. 1.1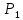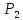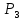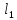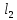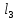
		кН				м
8	8	170	230	130		1,2	1,5	1,1
9	9	180	240	140		1,3	1,6	4,1
0	0	190	250	150		1,4	1,7	1,3
	В	Б	В	Б		А	Б	В
	0	9	0	9		8	9	0

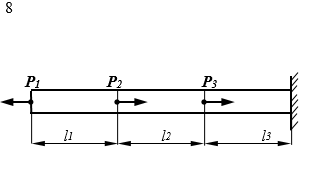
Рис. 1.1

1. Для построения эпюры продольных сил 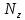надо знать все приложенные к брусу силы, к которым относятся заданные нагрузки и опорные реакции.

Определяем опорную реакцию в заделке (рис. ). При рассматриваемой схеме нагружения реакция заделки имеет только горизонтальную составляющую 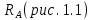. Для определения ее численного значения используем условие равновесия :

---

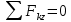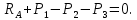
Следовательно,



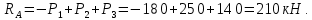
Определяем продольные силы . Разобьем брус на участки I, II, III и воспользуемся методом сечений (рис. 1.3а ). Напомним, что при составлении аналитического выражения для суммируются силы, находящиеся по одну сторону от сечения, причем силы, направленные от сечения, считаются положительными, а направленные к сечению – отрицательными. С учетом сказанного получаем:

– участок I

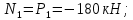
– участок II

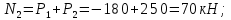
– участок III

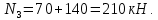
Строим эпюру 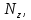т. е. график, показывающий изменение продольной силы по длине бруса. Выбираем масштаб эпюры и откладываем на каждом участке положительные значения 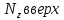, отрицательные – вниз. Эпюра показана на рис. 1.2 б.

2. Определяем площадь поперечного сечения бруса.

Условие прочности при растяжении



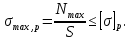
Для обеспечения прочности растянутых участков бруса площадь поперечного сечения



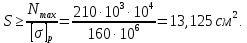
Из условия прочности при сжатии



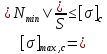
площадь поперечного сечения сжатых участков должен составить



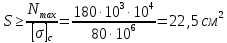
Так как сечение бруса по его длине постоянное, то, для обеспечения прочности всех участков, окончательно следует выбирать большую площадь, т. е. S = 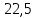см².

3.Определям напряжения в поперечных сечениях бруса:







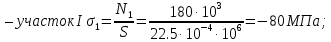
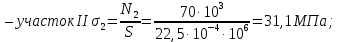
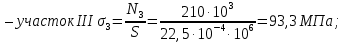
По полученным значениям строим эпюру

---

Смотрите также файлы

• Задание 1 по учебному курсу Философия права.docx

• Методические рекомендации по написанию выпускной квалификационной работы Уровень высшего образования магистратура направление подготовки.doc

• Курсовая работа Название дисциплины Сопровождение и продвижение программного обеспечения отраслевой направленности Тема.odt

• Цена деления прибора C, мм.docx

• ыфв.docx