Файл: Контрольная работа По дисциплине Физика (часть1) Перфильев С. Е. Группа мбт22 Вариант 6 Новосибирск, 2022 г.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 80
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Контрольная работа
По дисциплине: Физика (часть-1)
Выполнил: Перфильев С.Е.
Группа: МБТ-22
Вариант: 6
Новосибирск, 2022 г
-
Радиус-вектор материальной точки изменяется со временем по закону: , где векторы
, где векторы  являются ортами декартовой системы координат. За третью секунду движения равнодействующая сила совершила работу 6,4 Дж. Чему равна масса данной материальной точки?
являются ортами декартовой системы координат. За третью секунду движения равнодействующая сила совершила работу 6,4 Дж. Чему равна масса данной материальной точки?
Дано
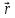 (t) =
(t) = 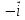 + 0,4
+ 0,4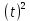
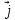
 + 0,9t
+ 0,9t 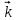
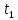 = 2 c
= 2 c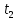 = 3 c
= 3 cA = 6,4 Дж
Найти
m - ?
Решение
Воспользуемся теоремой о кинетической энергии
Мгновенная скорость по определению есть первая производная по времени
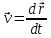
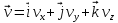 , где
, где 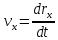 ,
, 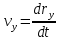 ,
, 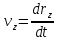 – проекции вектора скорости на соответствующие координатные оси x, y, z.
– проекции вектора скорости на соответствующие координатные оси x, y, z.Величина (модуль) скорости определяется соотношением
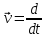 (
( + 0,4
+ 0,4

 + 0,9t
+ 0,9t  ) = 0,8t
) = 0,8t + 0,9
+ 0,9
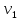 =
= 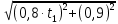
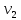 =
= 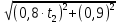 (2)
(2)Выразим массу из (1) и подставим выражения (2)
2А = m (
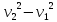 )
)m =
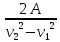
m =
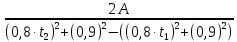 =
= 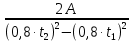 =
= 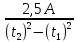
m =
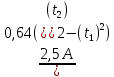
m =
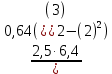 = 5 (кг)
= 5 (кг)-
Шар массой 1 кг, движущийся горизонтально со скоростью 1, столкнулся с неподвижным шаром меньшей массы и потерял при этом 80% своей кинетической энергии. Какова масса второго шара? Удар прямой абсолютно упругий, центральный.
Дано
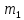 = 1 кг
= 1 кг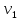 =
= 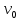
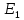 = 0,2
= 0,2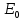
Найти
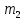 - ?
- ?Решение
Центральный удар двух шаров – это удар, при котором шары движутся вдоль прямой, проходящей через их центры, никаких изменений в направлении перпендикулярном Х не будет, соответственно
взаимодействие тел можно не учитывать.
До удара
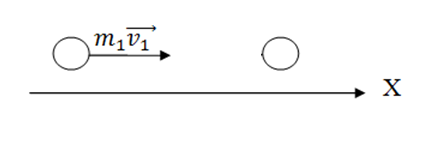
После удара
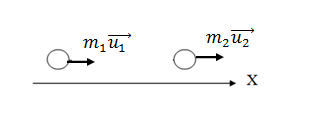
Запишем закон сохранения импульса (импульс замкнутой системы до взаимодействия равен импульсу системы после взаимодействия
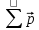 = const)
= const)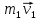 +
+ 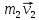 =
=  +
+ 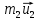 ,
, 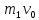 +
+  =
= 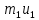 +
+ 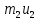 (1)
(1)Так как удар абсолютно упругий, то выполняется закон сохранения механической энергии, сумма кинетических энергий до удара = сумме кинетических энергий после удара. Кинетическая энергия по определению
Е =
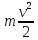 , здесь m – масса тела,
, здесь m – масса тела, 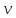 - скорость тела.
- скорость тела.Запишем закон сохранения
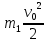 =
= 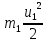 +
+ 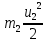 согласно условию
согласно условию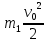 =
= 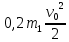 +
+ 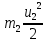
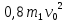 =
= 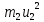 ,
, 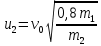 (2)
(2)Кроме того
 = 0,2
= 0,2
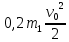 =
= 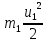
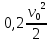
=
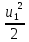 ,
, 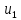 =
= 
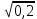 (3)
(3)Из (1) выразим массу второго шара
 -
-  =
= 
 =
= 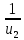 (
(  -
-  ) , подставим сюда (3) и (2)
) , подставим сюда (3) и (2) =
= 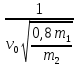 (
(  -
- 
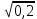 ) =
) = 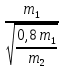 (1-
(1- 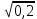 )
) =
= 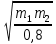 (1-
(1-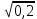 )
)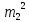 =
= 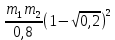
 =
= 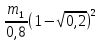
 =
= 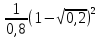 = 0,381966
= 0,381966 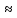 0,38 (кг)
0,38 (кг)Ответ:

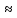 0,38 кг
0,38 кг-
Два очень длинных непроводящих концентрических (с общей осью) цилиндра радиусами R и 2R заряжены с поверхностной плотностью зарядов 1 и 2 соответственно. Найти силу (модуль и направление), действующую на электрон, находящийся в точке r1 = 3R от оси цилиндров. Какая работа будет совершена при перемещении электрона из этой точки на внешнюю поверхность большего цилиндра? Принять R = 0,1 м, 1 = 2 нКл/м2, 2 = 3 нКл/м2.
Дано
ε = 1
q = 1,6
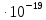 Кл
Кл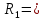 R
R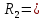 2R
2R r = 3R
R = 0,1 м
1 = 2 нКл/м2
2 = 3 нКл/м2
Найти
A - ?
F - ?
Решение
Определим напряженность поля в заданной условием точке

система находится в среде с ε = 1
Проведем коаксиальную цилиндрическую поверхность радиуса S радиусом R и воспользуемся теоремой Остроградского—Гаусса.
Из соображений симметрии нормальная составляющая En должна быть равна самой искомой напряженности и постоянна для всех точек окружности (сечения цилиндрической поверхности), т. е. En =E =const.
Так как внутри этой поверхности находится, заряд (Q1 + Q2 ) то для нее, согласно теореме Остроградского—Гаусса, можно записать равенство
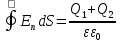
ES =
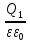
площадь цилиндра S =
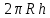 ,
, заряды цилиндров
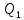 =
= 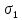
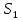 =
= 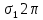
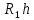 ,
, 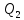 =
= 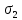
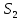 =
= 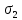
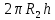
Е =