Закон действия и противодействия

(III-й закон Ньютона, аксиома взаимодействия тел в статике)



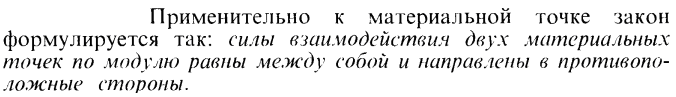
Динамика материальной точки







Иными словами, в случае несвободной материальной точки, левая часть уравнения , кроме заданных сил, должна также содержать реакции отброшенных связей.
Решение задач на применение основных законов динамики



















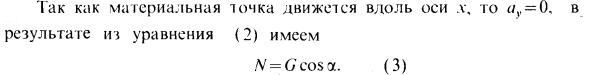
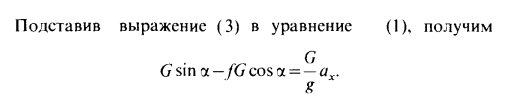
Понятие о силах инерции. Метод кинетостатики.

---

Принцип Д ' Аламбера.

Пусть на материальную точку М действует некоторая система сил , , … . Среди этих сил могут быть активные силы и реакции связей (рис. 1).

Н а основании принципа независимости действия сил точка М под действием этих сил получит такое же ускорение, как если бы на нее действовала, лишь одна сила, равная геометрической сумме заданных сил:

,

где – ускорение точки М; m – масса точки М – главный вектор системы сил.

Перенесем вектор, стоящий в левой части уравнения, в правую часть. После этого получим сумму векторов, равную нулю:

.

Введем обозначение, , тогда приведенное уравнение можно представить в виде:

. (*)

Так как силы равны между собой и направлены по одной прямой в противоположные стороны, то система сил , , …, , будет уравновешенной.

Сила , равная произведению массы материальной точки на ее ускорение

---

, но направленная в сторону, противоположную ускорению, называется силой инерции.

Сила в уравнении (*) является фиктивной (условной). Однако её приложение к ускоренно движущейся материальной точке позволяет уравновесить все действующие на неё активные и реактивные силы.

Уравнение (*) является математической формой записи принципа Д'Аламбера:

«Если ко всем действующим силам, приложенным к материальной точке, приложить силу инерции, то полученную систему сил можно рассматривать в состоянии мгновенного равновесия».

Применение принципа Д'Аламбера позволяет при решении динамических задач использовать уравнения равновесия сил из статики. Иными словами, позволяет решать задачи динамики методами статики. Такой метод в решении решения задач динамики называется кинетостатическим

Следует подчеркнуть, что силы инерции материальны и действительно существуют. Однако они приложены не к движущемуся телу, а к его «связям», то есть к телам, которые стремятся разогнать или замедлить рассматриваемое тело.

Рассмотрим, как определяется сила инерции материальной точки в различных случаях её движения

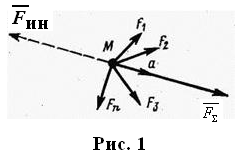
1 . Точка М массой m движется прямолинейно со скоростью и ускорением (рис. 2).

При ускоренном движении направление совпадает с . Сила инерции направлена в сторону, противоположную ускорению и .

При замедленном движении вектор направлен противоположно скорости . Сила инерции направлена в сторону, противоположную ускорению

---

, но совпадает с вектором .

Модуль в обоих случаях находится по формуле .

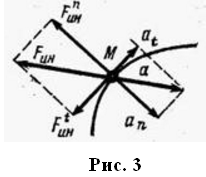
3. Точка М движется криволинейно и неравномерно (рис. 3)

У скорение точки раскладывается на нормальную и касательную составляющие.

Сила инерции точки также раскладывается на нормальную и касательную составляющие. Векторы , направлены противоположно и соответственно.

Полная сила инерции точки М и её модуль находится по формулам:

,

.

Полученные формулы также применимы и при движении точки по окружности (частный случай криволинейного движения).
Принцип Д ' Аламбера

(практика)
Порядок решения задач с использованием принципа Д'Аламбера

1. 
   Составить расчетную схему.
   
2. 
   Выбрать систему координат.
   
3. 
   Выяснить направление и величину ускорения.
   
4. 
   Условно приложить силу инерции.
   
5. 
   Составить систему уравнений равновесия.
   
6. 
   Определить неизвестные величины.
   

---

Задача 2

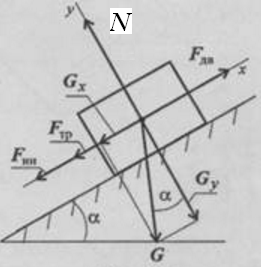
Тело весом 3500 Н движется вверх по наклонной плоскости согласно уравнению S =0,16∙t2 (см. рисунок). Определить величину движущей силы, если коэффициент трения тела о плоскость f = 0,15.

Р ешение

1. Составим расчетную схему. Прикладываем к телу действующие на него силы.

Активные силы: движущая , сила трения , сила тяжести (по модулю равна весу телу).

Реактивные силы: реакция наклонной плоскости.

2. Выбираем систему координат. Ось Ох направим вдоль наклонной плоскости вниз. Ось Оy – перпендикулярно наклонной плоскости вверх.

3. Определяем величину и направление ускорения тела.

Для этого воспользуемся уравнением движения тела. Поскольку тело движется прямолинейно,

; ; .

Следовательно, движение тела равноускоренное. Векторы и направлены в сторону движения.

4. Для определения модуля воспользуемся принципом Д'Аламбера. Добавим к действующим на тело активным и реактивным силам фиктивную силу инерции .

Вектор направлен противоположно ускорению .

---

Смотрите также файлы

• Работа с sql бд в Webприложениях Node js.docx

• Особенности игровой деятельности глухих и слабослышащих детей Игровая деятельность глухих и слабослышащих детей.ppt

• Дисциплина Русский язык Практическое занятие 5 Обучающийся Квитчук Виктория Олеговна Преподаватель Луковникова Ольга Юрьевна Задание 2.rtf

• Нефтеперерабатывающий завод.docx

• Федеральное государственное бюджетное образовательное учреждение высшего образования Башкирский государственный медицинский университет Министерства здравоохранения Российской Федерации.docx