Файл: Закон действия и противодействия (iiiй закон Ньютона, аксиома взаимодействия тел в статике) Динамика материальной точки.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 33
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
З
адача 3
Работа и мощность
Работа постоянной силы на прямолинейном участке
Работа переменной силы
В
общем случае, материальная точка движется по криволинейной траектории и на неё действует переменная по модулю и направлению сила: 
, 
.Чтобы найти работу переменной силы
разобьем пройденный путь S на n элементарных отрезков пути 
(рис. 3).На элементарные отрезке
криволинейный путь материальной точки можно считать прямолинейным, а силу 
постоянной (
, 
).Работа на элементарном отрезке пути
: 
Работа силы
на конечном пути s равна сумме элементарных работ
.Переходя к приделу
, запишем 
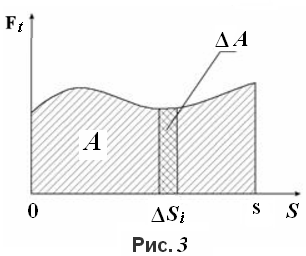
Из рис. 3 следует, что элементарная работа
равна площади полоски (элементарного прямоугольника 
). Следовательно, работа переменной силы 
на конечном пути s равна площади фигуры под кривой 
на отрезке [0; s]. Это выражает известный их математики геометрический смысл определённого интеграла на заданном отрезке
Работа силы тяжести.
Сила G имеет постоянный модуль и направление, однако, траектория её криволинейная.
Т
еорема о работе равнодействующей
С помощью формулы (3) определяется также мощность, развиваемая парой сил с моментом M = const, приложенной к вращающемуся телу.
С помощью формулы (6) определяется также мгновенная мощность, развиваемая парой сил с моментом M ≠ const, приложенной к вращающемуся телу.
Механический КПД
Действующие на тела силы можно разделить на движущие силы и силы сопротивления.
Движущие силы совершают положительную работу и стремятся ускорить движение тела.
Силы сопротивления совершают отрицательную работу и стремятся замедлить движение тел.
Эти силы делятся на силы вредного сопротивления (силы трения, силы сопротивления среды) и силы полезного сопротивления − силы, для преодоления которых предусмотрен технологический процесс машины.
Механический КПД – это безразмерная характеристика эффективности подводимой к механизму (машине) механической энергии за один рабочий цикл:
, (1)где
, 
, 
− работа движущих сил, а также сил полезного и вредного сопротивления. Так как всегда имеют место силы вредного сопротивления, то в каждый момент времени справедливы неравенства
, 
. Чем больше
, тем бо́льшая часть энергии расходуется в механизме на полезную работу, тем рациональнее используется механическая энергия.Энергия (в том числе механическая) − способность тела (машины, механизма) совершать работу при переходе из одного состояния в другое.
Поскольку работа силы за фиксированный отрезок времени пропорциональна среднему значению мощности за тоже время (А = P∙t), то формула приводится к виду:
, (2)где
, , − средняя мощность движущих сил, а также сил полезного и вредного сопротивления за один рабочий цикл машины. КПД не только для оценки степени совершенства машин. КПД используют и для того, чтобы определять эффективность любых сложных механических устройств, а также тех приспособлений, которые не относятся к машинам, однако воспринимают
, потребляют и отдают энергию.
К таковым относятся, к примеру, паровые котлы (в них осуществляется преобразование химической энергии сгорания топлива в тепловую энергии пара), электрических двигателей (в них электрическая энергия преобразуется в механическую), электрических осветительных приборов (в них электрическая энергия преобразовывается в световую) и т.п.
Когда возникает задача определения КПД сложного по своей конструкции устройства, которое состоит из некоторого количества узлов, агрегатов и механизмов, потребляющих энергию, то наиболее целесообразно вычислять не только общий КПД, но и КПД всех отдельных составных частей.
Рассмотрим, например, установку, предназначенную для освещения помещений. Она состоит из следующих частей: станция, вырабатывающая электроэнергию; электрические провода; лампы накаливания.
С практической точки зрения интересно выяснить не только то, какой именно коэффициент полезного действия имеет эта конструкция в целом, но и то, каков именно КПД двигателя, передающего вращение электрогенератору; самого электрогенератора; проводников электрической сети; ламп накаливания.
Это позволяет, помимо всего прочего, определить наименее эффективные с точки зрения затрат энергии компоненты системы и, по возможности, использовать вместо них те, которые имеют более высокий КПД (например, светодиодные светильники вместо ламп накаливания).
Коэффициент полезного действия машины, механизма или любого другого устройства, отдельные части которого последовательно потребляют передаваемую от одного компонента к другому энергию, равняется произведению КПД этих компонентов.
КПД механизмов всегда тем ниже, чем выше потери на трение.
Решение задач на определение работы, мощности и кпд
Задача 2
(работа равнодействующей)
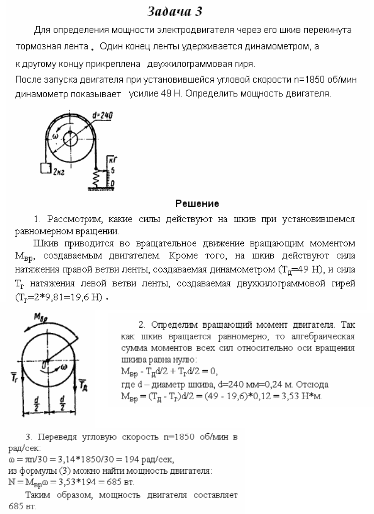
Задача 4
(мощность и КПД)
Задача 5
(мощность и КПД)
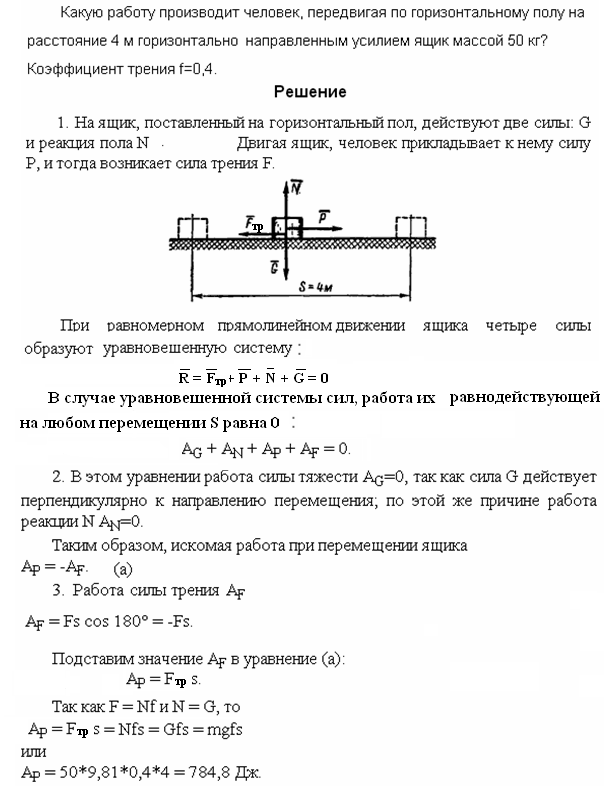
Тело М весом G = 500 Н силой P равномерно перемещается вверх по наклонной плоскости, длина которой l = 4 м и угол подъема α=20°. Определить работу, производимую силой, направленной параллельно наклонной плоскости, и коэффициент полезного действия наклонной плоскости. Коэффициент трения f = 0,2.
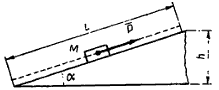
Решение.
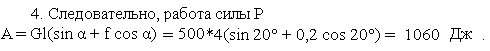
Задача 6
(принцип Даламбера)
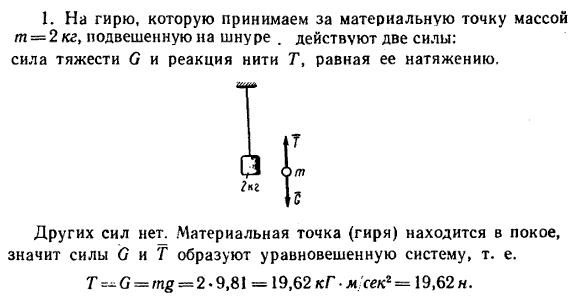
На шнуре подвешена гиря m = 2 кг. Определить натяжение шнура для следующих случаев:
1. груз находится в состоянии покоя;
2. груз движется вертикально вверх равномерно;
3. груз движется вертикально вверх с ускорением
.4. груз опускается с ускорением
.Решение:
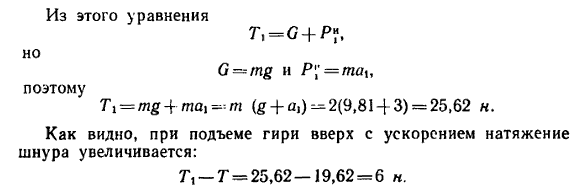
Задача 7
(принцип Даламбера)
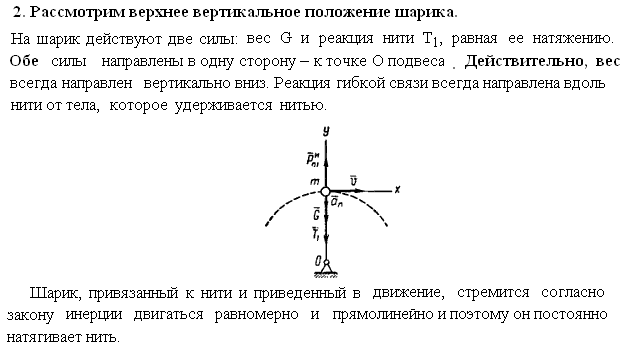
Шарик, масса которого m = 0,5 кг, привязан к нити длиной r = 0,7 м. Нить вместе с шариком вращается в вертикальной плоскости, затрачивая на один оборот 1 сек. Определить натяжение шнура в моменты высшего и низшего положения шарика, считая, что скорость остается постоянной при перемещении по всей длине окружности.
Решение.
