Рассмотрим несколько примеров применения метода непосредственного интегрирования приближенного уравнения упругой линии балки.

 

Пример 1

Определить стрелу прогиба и угол поворота сечения Вбалки, изображенной на рис.17.3



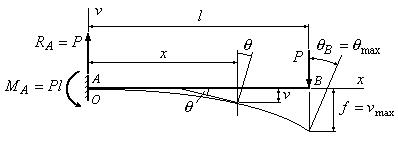
Рис.17.3

 

Решение.

1. Из условий равновесия определяем опорные реакции:



2. Выбираем начало координат O на левом конце балки, совмещая его с точкой А. ОсьOv направляем вверх, ось Ox  вправо.

3. Составляем уравнение изгибающего момента в сечении x:



4. Предполагая, что жесткость балки постоянна, записываем приближенное дифференциальное уравнение упругой линии балки:



Знак “+” в уравнении упругой линии был принят потому, что ось Ov направлена вверх.

5. Интегрируем уравнение первый раз. Получаем:



Интегрируя еще раз, получаем уравнение для прогиба в сечении x:



Так как в заделке прогиб и угол поворота равны нулю, то для определения постоянных интегрирования граничные условия имеют вид:

при x=0    θ(x)=0;

при x=0    v(x)=0.

Из уравнения (а) видно, что постоянная C представляет собой угол поворота в начале координат (сечении А). Задавая в уравнении (а) x=0, находим C=0. Из уравнения (б) следует, что постоянная D  прогиб в начале координат. Задавая в уравнении (б) x=0, получаем D=0.

Таким образом, получаем следующие выражения для прогиба и угла поворота:





Подставляя в первое уравнение x=l, найдем стрелу прогиба:

---

Подставляя во второе уравнение x=l, найдем максимальный угол поворота



Знак “” у прогиба свидетельствует о том, что его направление не совпадает с положительным направлением оси Oy. Знак “” в выражении угла поворота показывает, что сечение В повернулось не против, а по часовой стрелке.
 КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Что понимается под жесткостью 

2.Какое уравнение носит название приближенного дифференциального уравнения изогнутой оси упругой балки.

3.Какие величины называются начальными параметрами? 

---

Смотрите также файлы

• Желчнокаменная болезнь и ее осложнения.docx

• Сообщение На эл подстанции Чара произошло возгорание трансформатора, разлив гж в обвалование, площадь пожара 10 кв метров.docx

• Правовые основы физической культуры и спорта.docx

• 1. 3 Единая государственная система.docx

• Рабочая программа по английскому языку для 10 авг предмет курс класс на 2022 2023 учебный год.doc