Файл: Решение. Составим прямую задачу Определим максимальное значение целевой функции L(X) 4x.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 06.11.2023

Просмотров: 23

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.





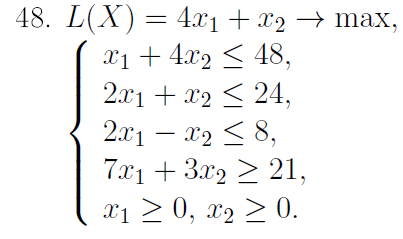
Решение.

Составим прямую задачу:

Определим максимальное значение целевой функции L(X) = 4x1 + x2 при следующих условиях-ограничениях:

x1 +4 x2≤48

2x1 + x2≤24

2x1 - x2≤8

7x1 + 3x2≥21

х1 ≥ 0

х2 ≥ 0

y1 + 2y2 + 2y3 + 7y4≥4

4y1 + y2 - y3 + 3y4≥1

F(y)=48y1 + 24y2 + 8y3 + 21y4 → min

y1 ≥ 0

y2 ≥ 0

y3 ≥ 0

y4 ≤ 0
Решим прямую задачу графическим методом.

Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).



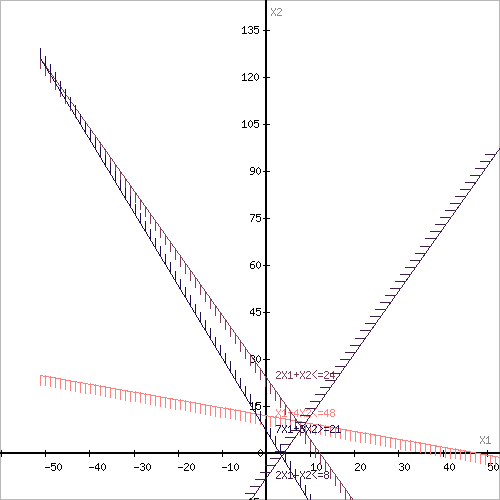
Границы области допустимых решений

Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.

Обозначим границы области многоугольника решений.



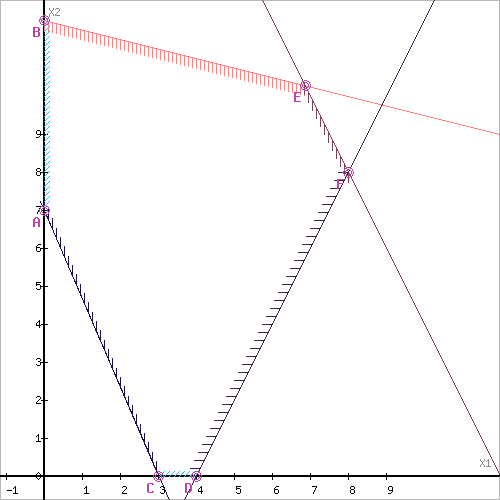
Рассмотрим целевую функцию задачи L = 4x1+x2 → max.

Построим прямую, отвечающую значению функции L = 0: L = 4x1+x2 = 0. Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.


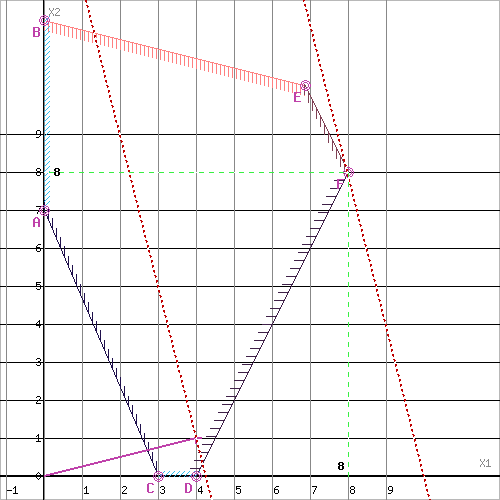
Область допустимых решений представляет собой многоугольник

Прямая L(x) = const пересекает область в точке F. Так как точка F получена в результате пересечения прямых 2x1+x2=24, 2x1-x2=8, то ее координаты удовлетворяют уравнениям этих прямых:

2x1+x2=24,

2x1-x2=8

Решив систему уравнений
, получим: x1 = 8, x2 = 8

Откуда найдем максимальное значение целевой функции:

L(X) = 4*8 + 1*8 = 40

Найдем решение двойственной задачи. Будем искать ее оптимальное решение, используя условие «дополняющей нежесткости».

Составим соотношения, удовлетворяющие второй теореме двойственности:



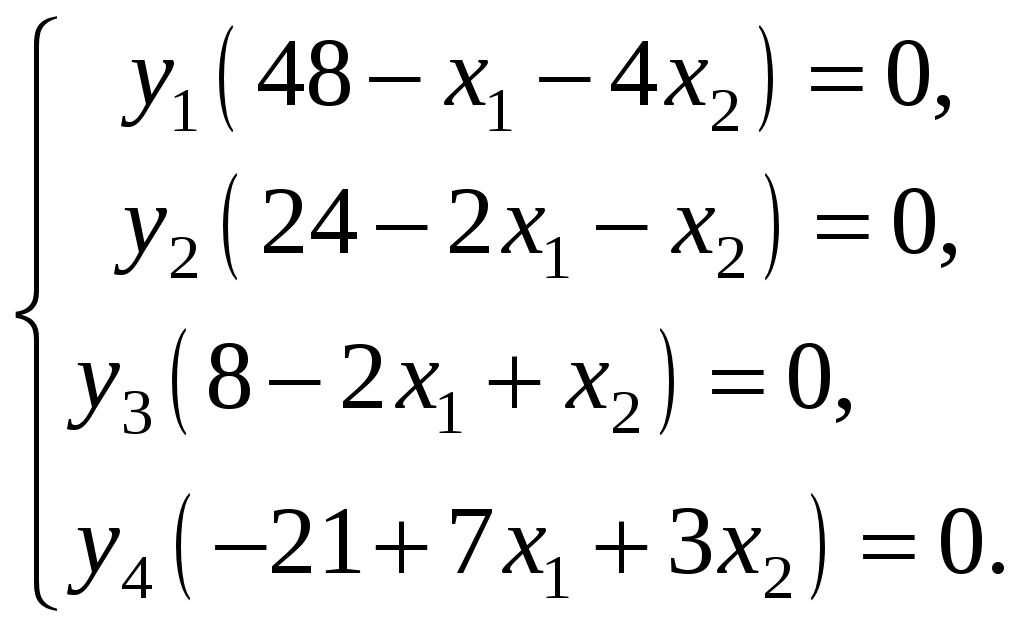
Подставляя в них найденные значения x1 = 8, x2 = 8, получим: .

Таким образом, получаем систему уравнений:

y1 + 2y2 + 2y3 + 7y4=4

4y1 + y2 - y3 + 3y4=1

y1=0

y4=0

Решая данную систему, получаем, что .

Таким образом, оптимальное решение двойственной задачи имеет вид: .

Минимальное значение целевой функции при этом 48*0+24*1,5+8*0,5+21*0 = 40

Смотрите также файлы