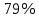Файл: Решение Введем полную группу гипотез (деталь изготовлена на первом станке).docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 06.11.2023

Просмотров: 148

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
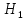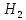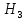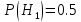
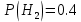
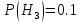
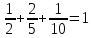
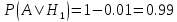
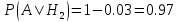
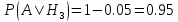
РешениеВведем полную группу гипотез: = (деталь изготовлена на первом станке), = (деталь изготовлена на втором станке), = (деталь изготовлена на третьем станке).Вероятности гипотез известны: КонтрольНаходим условные вероятности. 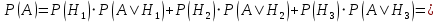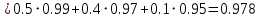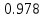То есть, предположив номер станка, находим вероятность того, что деталь, изготовленная на нем, окажется стандартнойПо формуле полной вероятности находим вероятность того, что наугад взятая деталь (из выпущенных всеми станками) будет стандартной Ответ: РешениеЕсли вероятность наступления события в каждом испытании постоянна, число испытаний велико и они независимы друг от друга, то при этих условиях можно использовать интегральную теорему Муавра-Лапласа. Эта теорема говорит о том, как вычислить вероятность наступления события от 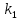до 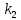раз, где 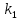и 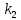- какие-то числа, но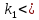

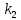
и меньше либо равно полному числу испытаний 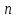. По интегральной теореме Лапласа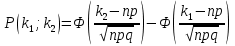



В этой формуле 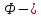функция Лапласа, ее значения при разных аргументах приведены в специальных таблицах, 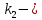максимальное число появлений события в 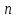испытаниях, 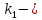минимальное число появлений события в 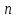испытаниях, 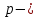вероятность появления события в каждом из 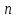независимых испытаний, 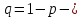вероятность, наоборот, непоявления события в каждом из 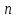независимых испытаний.

Максимальное и минимальное число появлений события в 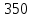независимых испытаниях по условию равны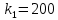





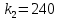
В нашем случае вероятность наступления события



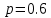
А вероятность ненаступления



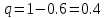
Тогда по интегральной теореме Лапласа искомая вероятность









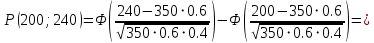
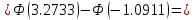
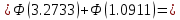
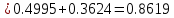
Ответ:




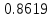
Решение

1)

Математическое ожидание служит характеристикой среднего значения случайной величины. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности

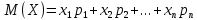
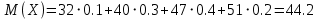
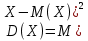
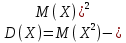
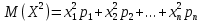
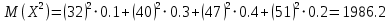
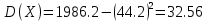
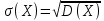
С учетом числовых данных 2)Дисперсией случайной величины X называют математическое ожидание квадрата отклонения случайной величины от ее математического ожиданияДисперсию удобно вычислять по формуле Математическое ожидание квадрата случайной величиныПроизведем вычисления Дисперсия равна3)Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии С учетом числовых данных 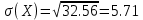Ответ:1) 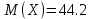2) 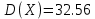3)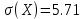РешениеЗаданы 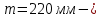математическое ожидание, 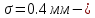среднее квадратическое отклонение.Найдем вероятность того, что максимальное отклонение будет меньше, чем По условию надо найти вероятность попадания случайной величины - длины детали на промежуток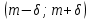Вероятность того, что нормальная случайная величина примет значение из интервала 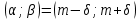можно вычислить по формуле:
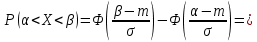
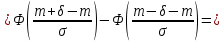
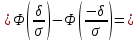
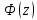
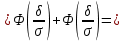
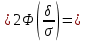
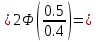
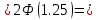
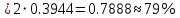
Пользуемся нечетностью функции Ответ:

Смотрите также файлы