ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 37
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М.А. Бонч-Бруевича
ФАКУЛЬТЕТ ВЕЧЕРНЕГО И ЗАОЧНОГО ОБУЧЕНИЯ
Контрольная работа за _3_ семестр
По дисциплине _Дискретная математика_
Вариант _3_
Фамилия:_Коломыц__________
Имя:_Денис_____________
Отчество:_Александрович_____
Курс:_2_________________
Студ. билет № :_1804103___________
Группа №:_РБ-11з____________
Дата сдачи работы:______________
Санкт-Петербург
20_23_
_ДМ, __Коломыц__, __РБ-11з__
| Рецензия 1 | Дата получения работы:_____________ | Рецензия 2 | Дата получения работы:_____________ | ||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| Оценка:_____________ | Баллы:_____________ | Оценка:_____________ | Баллы:_____________ | ||
| Дата: __________________ | Подпись преподавателя: _______________________ | Дата: ________________ | Подпись преподавателя: _______________________ | ||
| | | ||||
| Рецензия 3 | Дата получения работы:_____________ | Рецензия 4 | Дата получения работы:_____________ | ||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| №_________________________________________ ___________________________________________ | №_________________________________________ ___________________________________________ | ||||
| Оценка:_____________ | Баллы:_____________ | Оценка:_____________ | Баллы:_____________ | ||
| Дата: __________________ | Подпись преподавателя: _______________________ | Дата: ________________ | Подпись преподавателя: _______________________ | ||
3
3. Используя правила де Моргана, получить ДНФ и упростить:
.Решение.
.Получили ДНФ. Упростим эту формулу:
.Ответ:
13. Даны две функции f1(x,y), f2(x,y,z). Требуется:
а) для функции f1(x,y) составить таблицу истинности и найти по ней полином Жегалкина, СДНФ и СКНФ. Упростить, если возможно, СДНФ.
б) для функции f2(x,y,z) составить таблицу истинности и найти по ней полином Жегалкина, СДНФ и СКНФ. По карте Карно получить минимальную ДНФ, нарисовать эквивалентную РКС.
в) составить таблицу Поста для системы функций f1(x,y), f2(x,y,z), проверить полноту системы и выбрать базисы, если она полная.
, 
Решение.
а) Для функции
составим таблицу истинности:-
x
y
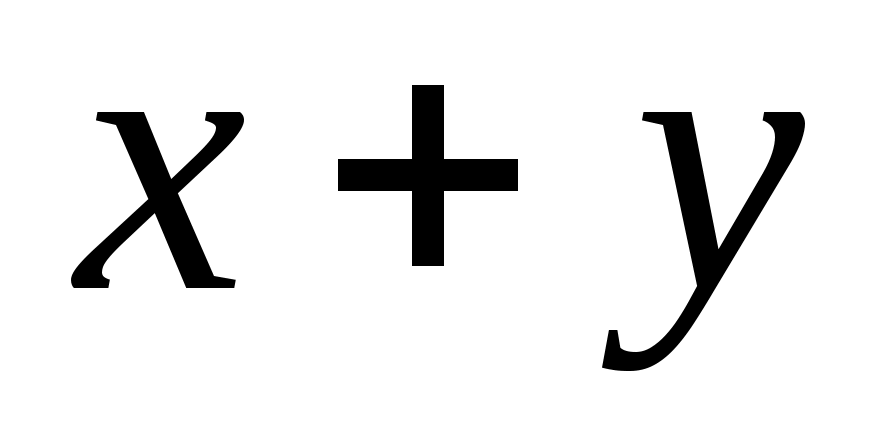
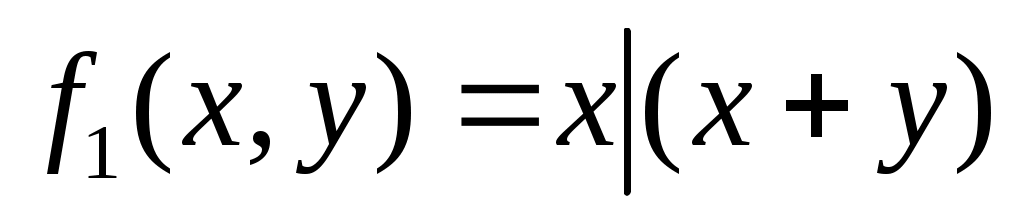
0
0
0
1
0
1
1
1
1
0
1
0
1
1
0
1
Найдём полином Жегалкина:
. Откуда получаем, что
.
. Откуда получаем, что 
.
. Откуда получаем, что 
.
. Откуда получаем, что 
.
4
По наборам таблице истинности, где
составим СДНФ
.Упростим СДНФ, используя склеивание по «
» и по «
»
.Составим СКНФ по наборам, на которых
:
.в
) Составим и заполним таблицу Поста:-
T0
T1
S
L
M
-
+
-
-
-
-
-
-
-
-
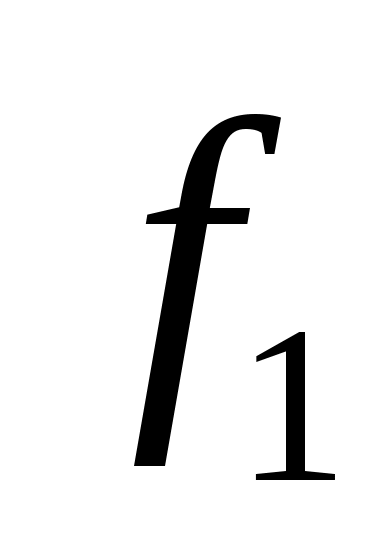
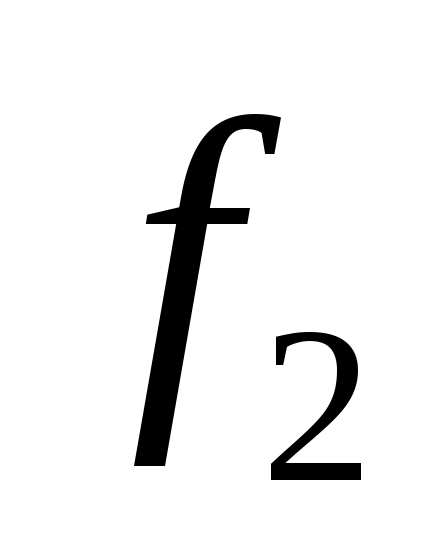
Так как:
, то 
и 
, то 
и 
Система функций полная, так как в таблице Поста все столбцы имеют хотя бы один минус. Проверяем на полноту каждую функцию:
- не составляет полной системы, так как нет функции не входящей в класс T1: 
- образует полную систему и является базисом, поскольку она не входит ни в один из пяти замкнутых классов.5
23. Для данного графа требуется составить структурную матрицу, по ней найти все простые пути из вершины i = 4 в вершину j = 1 и совокупность всех сечений между этими вершинами.
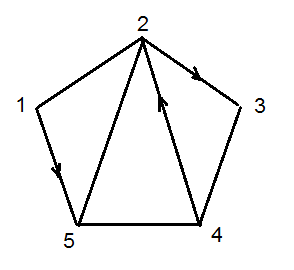
Решение.
Для данного графа составим структурную матрицу S, а затем вычеркнем из неё 1-ю строчку и 4-й столбец, тем самым получим минор M14:
, 
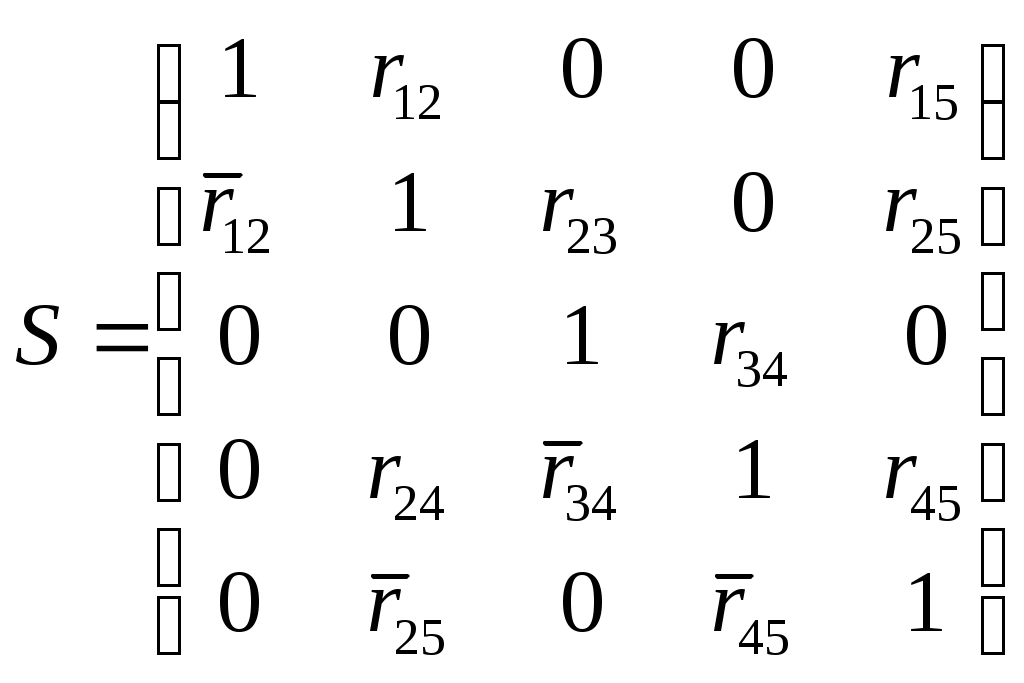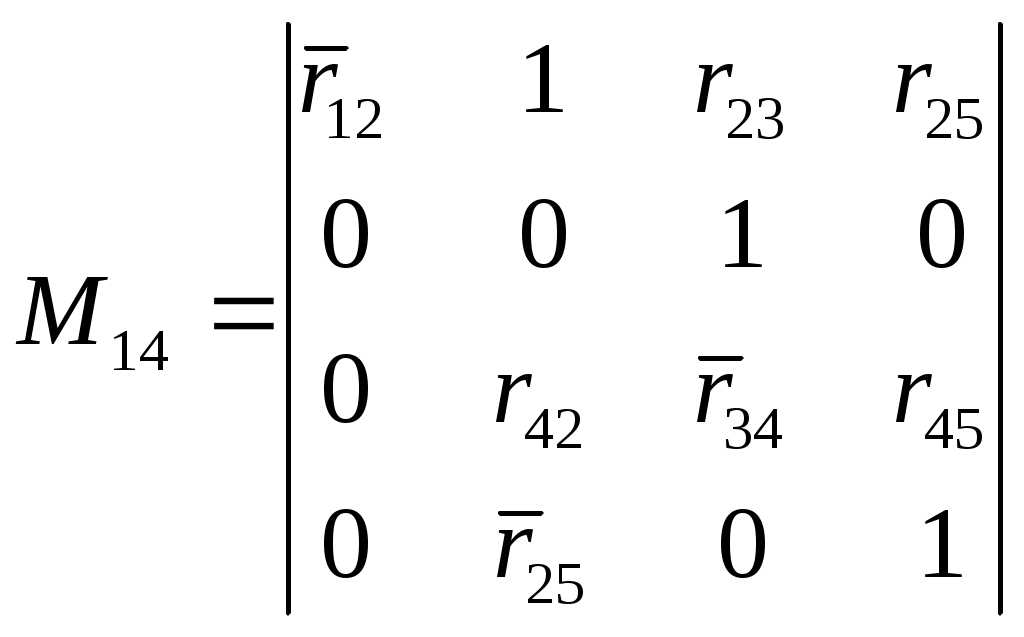.Найдём определитель, используя теорему разложения. Данный определитель разложим по 1-ому столбцу, поскольку он содержит три нулевых элемента:
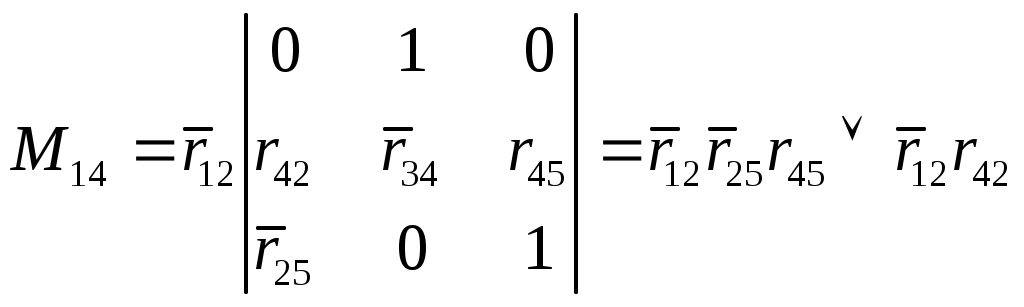.Граф содержит только два простых пути от вершины 4 к вершине 1:
и 
.Для нахождения сечений между вершинами i=4 и j=1 заменим дизъюнкцию на конъюнкцию, а конъюнкцию на дизъюнкцию и раскроем скобки.
.В результате получили три сечения:
, 
и 
.6
33. Задана сеть и начальный поток f. Требуется построить максимальный поток, считая вершину с номером 1 источником и вершину с номером 4 стоком. Указать минимальное сечение, величина которого равна максимальному потоку.
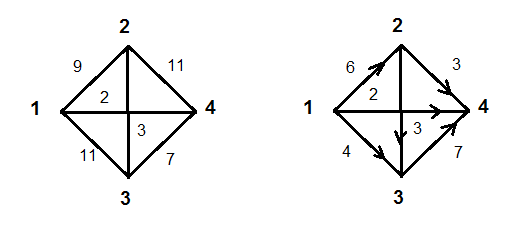
Решение.
Отметим, что мощность начального потока равна:
.Для исходного графа составим матрицу смежности с учетом пропускных возможностей дуг:
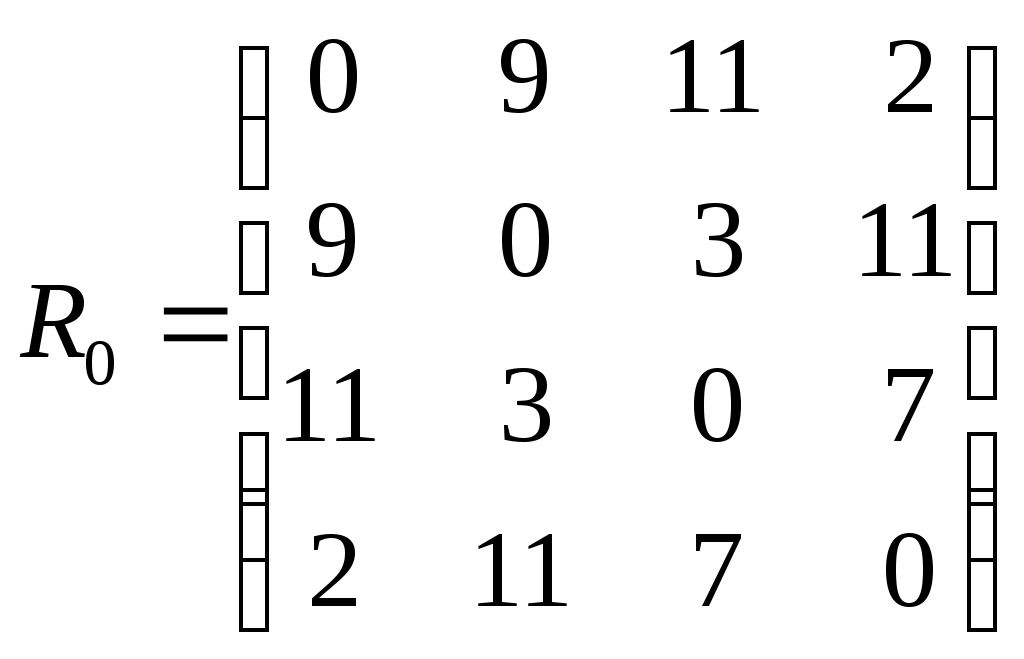. Пустим начальный поток 
и отобразим в матрице смежности изменения пропускных возможностей дуг сети: