ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 24
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Монотонность.
Функция
, определенная на множестве 
, называется возрастающей на этом множестве, если из того, что 
следует, что 
. Если последнее неравенство строгое для всех пар точек из , связанных условием 
, то функция называется строго возрастающей. Аналогично определяется убывающая и строго убывающая на функция. В обоих случаях мы говорим о монотонной или строго монотонной на функции.Пример 1.
Функции
и 
монотонны на промежутке 
. При этом первая возрастает на этом промежутке, а вторая — убывает. Функция 
монотонна (строго убывает) на каждом из лучей: 
и 
, но не является монотонной на всей области определения.Геометрический смысл производной дает основания предполагать, что если производная функции
в некоторой точке 
положительна, то существует окрестность точки
, внутри которой функция возрастает. Однако, как показывает следующий пример, в общем случае это неверно.
Пример 2.
Пусть
при 
, 
(см. рисунок справа).
В то же время
.Нетрудно заметить, что производная вблизи нуля принимает как положительные, так и отрицательные значения и, следовательно, функция не может постоянно возрастать ни на каком интервале, содержащем 0.
Тем не менее в некотором, более слабом смысле, возрастание все же есть.
Лемма о возрастании в точке.
Пусть функция
определена на некотором интервале, содержащем точку , дифференцируема в точке и в этой точке производная положительна, то есть 
. Тогда существует окрестность 
этой точки такая, что:
Чтобы получить возрастание на промежутке, нужны более сильные условия.
Теорема о монотонности на интервале. Пусть функция
определена на интервале
, причем в каждой точке интервала 
производная существует и положительна. Тогда функция строго возрастает на 
.Оценить изменение функции на заданном отрезке можно с помощью формулы конечных приращений, которая является результатом следующего важного утверждения.
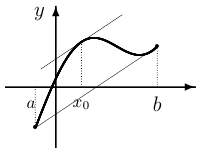
Теорема Лагранжа. Если функция
непрерывна на отрезке 
и дифференцируема на интервале , то в этом интервале найдется точка , такая что
Пример 3.
Оценить число
, считая, что 
.Решение:
Производная функции
равна 
. Используя формулу конечных приращений при 
, получим 
, где 
. Таким образом, 
. С другой стороны, 
. Следовательно,
.Пример 4.
Используя, что
, оценить с помощью теоремы Лагранжа число 
.Решение:
Используем вновь формулу конечных приращений, считая, что
. Поскольку 
. Следовательно,
«Настоящее» значение числа
приблизительно равно 0, 588.Пример 5.
Доказать, что при
выполняются неравенства
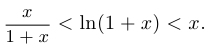
Решение:
Обозначим
и применим формулу конечных приращений (теорему Лагранжа):
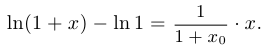
Поскольку
, получаем требуемые неравенства.Экстремумы функций
Содержание.
1. Введение
2. Историческая справка
3. Экстремумы функций одной переменной.
3.1. Необходимое условие
3.2.1. Достаточное условие. Первый признак
3.2.2. Достаточное условие. Второй признак
3.3. Использование высших производных
4. Экстремумы функций трех переменных.
4.1. Необходимое условие
4.2. Достаточное условие
5. Экстремумы функций многих переменных.
5.1. Необходимое условие
5.2. Достаточное условие
5.3. Метод вычисления критериев Сильвестера
5.4. Замечание об экстремумах на множествах
6. Условный экстремум.
6.1. Постановка вопроса
6.2. Понятие условного экстремума
6.3. Метод множителей Лагранжа для нахождения точек условного экстремума
6.4. Стационарные точки функции Лагранжа
6.5. Достаточное условие
7. Заключение
8. Библиография
Цель данного дипломномного проекта заключается в рассмотрении экстремумов функции одной и многих переменных и подробном описании методов их нахождения.
Задача состоит в формулировании необходимых и достаточных условий существования максимума и минимума функции, выборе метода нахожденя экстремумов и их полном математическом обосновании.
Гипотезой дипломного проекта является рассмотрение и описание экстремумов функции трёх переменных, формулировании необходимого и достаточного условия их существования, а также рассмотрение метода вычисления критериев Сильвестера.
В качестве объекта для исследования и описания использовались функции одной и многих переменных.
1.Введение.
Вмире не происходит ничего, в чем бы не был виден
Смысл какого-нибудь максимума или минимума.
Л.Эйлер.
В математике изучение задач на нахождение максимума и минимума началось очень давно. Но только лишь в эпоху формирования математического анализа были созданы первые методы решения и исследования задач на экстремум.
Потребности практической жизни, особенно в области экономики и техники, в последнее время выдвинули такие новые задачи, которые старыми методами решить не удавалось. Надо было идти дальше.
Потребности техники, в частности космической, выдвинули серию задач, которые также не поддавались средствам вариационного исчисления. Необходимость решать их привела к созданию новой теории, получившей название теории оптимального управления. Основной метод в теории оптимально управления был разработан в пятидесятые – шестидесятые годы советскими математиками – Л.С. Понтрягиным и его учениками. Это привело к тому, что теория экстремальных задач получила новый мощный толчок к дальнейшим исследованиям.
Цель дипломного проекта – рассмотрение и описание функций одной и многих переменных, а также в рассмотрении методов, используемых при этом.