ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 71
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В данном разделе выясним, как аналитически найти главный вектор и главный момент произвольной пространственной системы сил, установим аналитические условия ее уравновешивания, а также рассмотрим возможные частичные случаи возведения этой системы сил.
12. Момент силы относительно оси.
Определение: моментом силы относительно оси называется момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.
Согласно определению
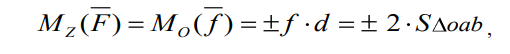
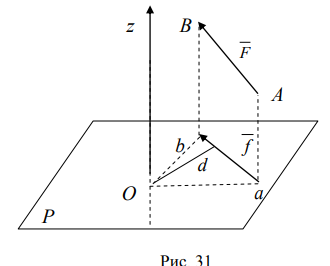
Правило знаков: если наблюдатель расположен со стороны положительного направления оси z и видит вращение плоскости Р вокруг оси z под действием силы f , происходящим против хода часовой стрелки, то момент силы F относительно оси считается положительным. Если наблюдатель видит вращение по часовой стрелке, то
Момент силы относительно оси равен нулю
в двух случаях:-
Проекция силы на плоскость, перпендикулярную оси, равна нулю (f = 0), в этом случае сила F и ось z параллельны. -
Плечо проекции силы равно нулю (d = 0), тогда линия действия силы пересекает ось.
Оба этих случая можно объединить в один: момент силы относительно оси равен нулю тогда и только тогда, когда сила и ось лежат в одной плоскости
13. Условия и уравнения равновесия пространственной системы сил.
Условие равновесия пространственной системы сил.
Произвольной пространственной системой сил называется система сил линии действия которых не лежат в одной плоскости.
Согласно основной теоремы статики (теореме Пуансо), любую произвольную систему сил, действующих на твердое тело, можно заменить эквивалентной системой, состоящей из силы (главного вектора системы) и пары сил (главного момента сил).
Отсюда вытекает условие равновесия произвольной пространственной системы сил:
В геометрической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент системы равнялись нулю.
В аналитической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на три координатные оси и суммы моментов всех сил относительно этих осей были равны нулю.
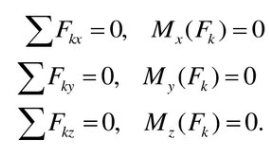
Условие равновесия могут быть использованы для решения задач на равновесие при определении неизвестных величин (реакций связей).
Чтобы задача была статистически определимой, число неизвестных должно быть не более 6.
В частности для системы параллельных сил условиями равновесия являются следующие равенства
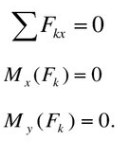
14. Центр параллельных сил и центр тяжести тела.
Центром параллельных сил называется точка, при повороте вокруг которой всех сил системы на один и тот же угол, линия действия равнодействующей системы параллельных сил повернется в ту же сторону на тот же угол.
Рассмотрим систему параллельных сил {F1, F2, …, Fn}. При повороте всех сил системы на один и тот же угол линия действия равнодействующей системы параллельных сил повернется в ту же сторону на тот же угол вокруг некоторой точки
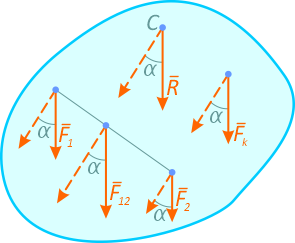
Эта точка является центром параллельных сил.
Согласно теореме Вариньона, если система сил имеет равнодействующую, то ее момент относительно любого центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси).
Для определения координат центра параллельных сил воспользуемся этой теоремой.
Относительно оси x
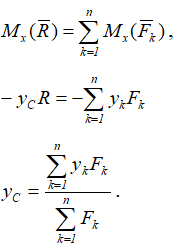
Чтобы определить координату zC, повернем все силы на 90° так, чтобы они стали параллельны оси y
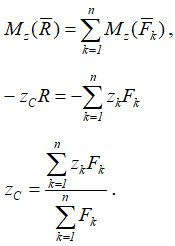
Следовательно, формула для определения радиус-вектора центра параллельных сил принимает вид
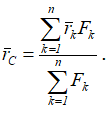
центр тяжести тела
Силы притяжения отдельных частиц тела к Земле направлены к центру Земли. Поскольку размеры рассматриваемых тел малы по сравнению с радиусом Земли, эти силы можно считать параллельными. Равнодействующая этих параллельных сил — это сила тяжести (ее модуль — это вес тела), а центр этой системы параллельных сил (в котором всегда приложена сила тяжести) называется центром тяжести тела. Поворот тела относительно Земли приводит к повороту системы сил относительно самого тела. При этом положение центра тяжести тела не зависит от расположения тела в пространстве.
Если обозначить модули сил тяжести отдельных частей тела G1 G2 Gn вес тела
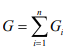, то радиус-вектор и координаты центра тяжести могут быть вычислены по общей формуле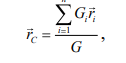 
из которой следует, что
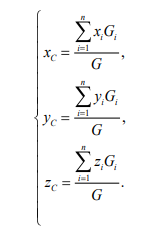
15. Центр параллельных сил.
Центром параллельных сил называется точка, при повороте вокруг которой всех сил системы на один и тот же угол, линия действия равнодействующей системы параллельных сил повернется в ту же сторону на тот же угол.
Рассмотрим систему параллельных сил {F1, F2, …, Fn}. При повороте всех сил системы на один и тот же угол линия действия равнодействующей системы параллельных сил повернется в ту же сторону на тот же угол вокруг некоторой точки
Эта точка является центром параллельных сил.
Согласно теореме Вариньона, если система сил имеет равнодействующую, то ее момент относительно любого центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси).
Для определения координат центра параллельных сил воспользуемся этой теоремой.
Относительно оси x
Чтобы определить координату zC, повернем все силы на 90° так, чтобы они стали параллельны оси y
Следовательно, формула для определения радиус-вектора центра параллельных сил принимает вид
16. Центр тяжести тела, объема, площади и линии.
центр тяжести тела
Силы притяжения отдельных частиц тела к Земле направлены к центру Земли. Поскольку размеры рассматриваемых тел малы по сравнению с радиусом Земли, эти силы можно считать параллельными. Равнодействующая этих параллельных сил — это сила тяжести (ее модуль — это вес тела), а центр этой системы параллельных сил (в котором всегда приложена сила тяжести) называется центром тяжести тела. Поворот тела относительно Земли приводит к повороту системы сил относительно самого тела. При этом положение центра тяжести тела не зависит от расположения тела в пространстве.
Если обозначить модули сил тяжести отдельных частей тела G1 G2 Gn вес тела
, то радиус-вектор и координаты центра тяжести могут быть вычислены по общей формуле 
из которой следует, что
Для однородного тела объемом V вес Pk любой его части объема
составляетгде γ - вес единицы объема, а вес всего тела
координаты центра тяж тела:
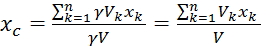; yc;zc(1.1)С- центром тяжести объема V.
для однородной плоской пластины площади
, получим ее координаты центра тяжести: 
;yc;(1.2)где xk,yk- координаты к-й части пластины площади
и координаты центра тяжести S.Точно так же можно найти координаты центра тяжести линии длиной L:
; yc;zc;17. Способы определения центра тяжести тела. Примеры.
способы определения координат центров тяжести однородных тел.
1)Способ симметрии. Если однородное тело имеет плоскость, ось или центр симметрии, то центр тяжести С лежит соответственно в плоскости, на оси или центре симметрии тела.
2)Способ разбиения. Если однородное тело можно разбить на конечное число частей, положения центров тяжести которых известны, то координаты центра тяжести всего тела можно определить по формулам (1.1) – (1.2), где n соответствует числу частей, на которые разбивается тело.
3)Способ дополнения. Этот способ применяется к телам, имеющим вырезы, когда объем (площадь) данного тела можно представить как разность объемов (площадей) тел. Причем положения центра тяжести тела без выреза и вырезанной части известны. В этом случае объем (площадь) тела без выреза считается положительным, а объем (площадь) вырезанной части – отрицательным.
4)Способ интегрирования. Если тело нельзя разбить на конечное число частей, положения центров тяжести которых известны, то его разбивают на бесконечное число элементарных объемов (площадей, линий). Тогда координаты центров тяжести тел можно получить с помощью формул (1.1) – (1.3), в которых суммы переходят в соответствующие интегралы
18. Кинематика точки.
В кинематике изучается движение материальных объектов (точки, твердого тела, сплошной среды) без рассмотрения причин, вызывающих или изменяющих это движение. Такое изучение движения материальных объектов не требует учета материальных характеристик этих объектов — массы, моментов инерции и др.
В кинематике рассматривают такие характеристики движения, как скорость и ускорение точки, угловые скорость и ускорение твердого тела и др.
Движение материальных объектов, в частности материальной точки, совершается в пространстве при изменении времени. Пространство в классической механике считается эвклидовым, не зависящим от времени и движущихся в нем материальных объектов. Время принимается универсальным, не связанным с пространством и не зависящим как от движения наблюдателя, с точки зрения которого рассматривается движение материального объекта, так и от движения самого материального объекта.
Движение материального объекта всегда следует рассматривать относительно какого-либо твердого тела — тела отсчета, т.е. движение является относительным. С телом отсчета скрепляют систему осей координат, например декартовых, принимая ее за систему отсчета, относительно которой рассматривается движение материального объекта. Системой отсчета для трехмерного эвклидова пространства не может служить одна точка, линия или плоскость, а должны быть три оси, не обязательно прямолинейные, но не лежащие в одной плоскости.
Независимость времени от движения означает, что во всех системах отсчета, произвольно движущихся друг относительно друга, оно одно и то же, если за начало отсчета выбрано общее для них событие.
В кинематике сплошной среды телами отсчета, относительно которых рассматривается движение, могут быть также деформируемые тела.
В курсе теоретической механики обычно изучаются движение точки и твердого тела. Соответственно кинематика делится на кинематику точки и кинематику твердого тела. В настоящем курсе дополнительно излагаются также основы кинематики сплошной среды.