ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 73
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
6. Теорема Вариньона о моменте равнодействующей плоской системы сил.
Теорема. Момент равнодействующей относительно оси равен алгебраической сумме моментов составляющих сил относительно той оке оси.
Пусть даны пространственная система n произвольно расположенных сил, приложенных к телу, и равнодействующая этой системы F
Приложим к телу другую систему сил, равнодействующая которой
по модулю равна силе 
и направлена по той же линии действия в противоположную сторону.Сила
для данной системы является уравновешивающей силой и вместе с данными силами образует уравновешенную систему
Так как обе записанные выше системы эквивалентны нулю, т. е. уравновешены, то можно применить к ним любое условие равновесия, например
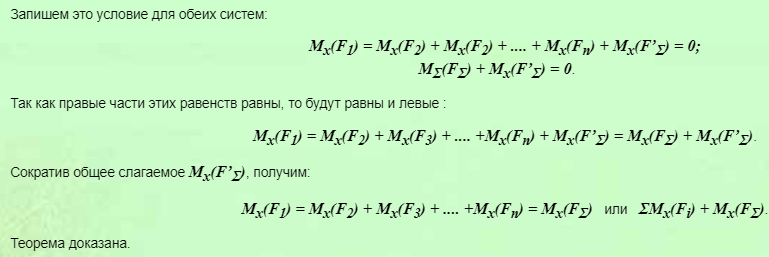
7. Теория пар сил на плоскости. Пара сил и ее момент. Теорема об эквивалентности пар на плоскости. Следствие.
Пару сил в механике рассматривают как одно из основных понятий наряду, с понятием силы.
Парой сил называют систему двух равных по модулю параллельных сил, направленных в противоположные стороны
Пара сил не составляет системы сил, эквивалентной нулю
Известно, что под действием пары сил свободное твердое тело выходит из равновесия. Обычно пару сил
прилагают к телу, которое должно вращаться, например к маховику вентиля при его закрывании и открывании (рис. 25). Поэтому пару сил нельзя заменить одной силой и, следовательно, она не имеет равнодействующей, а является такой системой сил, упростить которую нельзя. Каждая из сил, входящих в состав пары сил, имеет свойства обычных сил.Сила и пара сил представляют собой два базовых неупрощаемых элемента статики
Моментом пары F F’, называется вектор M F F’, , направленный перпендикулярно плоскости действия пары в такую сторону, чтобы, глядя навстречу ему, видеть вращение, осуществляемое парой, происходящим против часовой стрелки, и равный по модулю произведению модуля силы на плечо пары:
ТЕОРЕМА ОБ УСЛОВИЯХ ЭКВИВАЛЕНТНОСТИ ПАР
Две пары, имеющие векторно-равные моменты, эквивалентны друг другу. Справедливость этой теоремы равносильна справедливости следующих трех утверждений (трех более простых теорем). 1. Можно сделать любыми величины модулей сил и плеча пары, сохраняя их произведение, т. е. модуль момента пары. 2. Пару можно переносить в любое другое положение в плоскости ее действия (в пределах данного тела). 3. Пару можно переносить на параллельную плоскость действия. Приведем доказательство этих утверждений.
ни величина модуля силы, ни размер плеча, ни направление сил пары значения не имеют. Существенной характеристикой пары является только ее момент. Доказанные утверждения, позволяют преобразовывать и переносить пару, сохраняя при этом вектор ее момента неизменным
ВЫВОД: момент пары — вектор свободный. Он не связан с какой-либо точкой или линией действия и может быть перенесен параллельно в любую точку тела
8. Условия и уравнения равновесия плоской системы сил. Примеры.
Поскольку плоская система сил является частным случаем произвольной пространственной системы сил, для нее справедливы те же условия уравновешенности, что и для пространственной системы. Остановимся подробнее на записи условий уравновешенности в аналитической форме. Пусть плоскость в которой лежат линии действия сил системы
— это плоскость xy . Ось z перпендикулярна этой плоскости. Рассматривая шесть уравнений равновесия произвольной пространственной системы сил (7.4), легко видеть, что в данном случае уравнения 
превращаются в тождества, так как все силы перпендикулярны оси z и лежат в одной плоскости с осями x и y . Таким образом, условия уравновешенности плоской системы сил в аналитической форме будут представлены только тремя уравнениями:
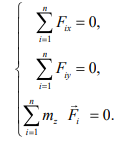
Последнее уравнение для плоской системы сил принято записывать иначе. Вместо того чтобы говорить о «моментах сил относительно оси z , проходящей через некоторую точку О, говорят о «моментах сил относительно точки О» и записывают последнее уравнение в виде:
Тогда уравнения равновесия для плоской системы сил принимают вид
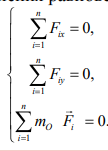
Это есть первая (основная) форма уравнений равновесия произвольной плоской системы сил.
Она состоит из двух уравнений проекций сил на две проведенные произвольным образом перпендикулярные оси х и у и одного уравнения моментов сил относительно произвольной точки О плоскости ху.
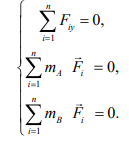
Это вторая форма уравнений равновесия плоской системы сил. Она содержит одно уравнение проекций сил на какую-либо ось y и два уравнения моментов сил относительно точек А и В (ось y не должна быть перпендикулярна линии АВ, иначе уравнения не будут независимы)
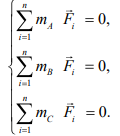Это третья форма уравнений равновесия плоской системы сил9. Равновесие при наличии трения.
Если тело находится в равновесии на шероховатой поверхности, полная реакция
такой опорной поверхности будет представлена двумя составляющими: нормальным давлением
и силой трения
(рис. 38). Величина предельной силы трения не зависит от размеров соприкасающихся поверхностей:
Равновесие при наличии трения качения.
При перекатывании одной криволинейной поверхности по другой возникает сопротивление, называемое трением качения. Если к катку приложить силу
(рис. 40 ), то вследствие деформации поверхности в месте контакта линия действия силы нормального давления
проходит на некотором расстоянии К от оси 
Максимальную величину К, соответствующую предельному положению равновесия, называют коэффициентом трения качения. Силы 
и
образуют пару сил, стремящуюся повернуть каток. Силы 
и образуют пару сил с моментом, препятствующим повороту катка. Момент этой пары
называют моментом трения качения. Трение качения возникает только при перекатывании упругих тел. Для качения абсолютно твердого катка по абсолютно твердой не деформируемой поверхности не потребуется никакой силы
10. Трение качения. Законы трения качения.
Трением качения называется трение движения, при котором скорости соприкасающихся тел в точках касания одинаковы по значению и направлению.
Трение качения наблюдается, когда одно тело перекатывается по другому и при повороте одного из которых относительно мгновенного или постоянного центра в контакт вступают новые участки поверхностей трения. Относительные скорости разных точек катящегося тела различны и определяются их удалением от контактной площадки
Трение качения встречается в подшипниках качения, парах колесо–рельс, ролик – транспортирующая лента конвейерных систем и др.
Различают чистое качение и качение с проскальзыванием. Чистое качение – контакт тел является идеально упругим и происходит по линии (для цилиндра) или в точке (для сферы).
Качение будет чистым, если при повороте тела на малый угол его ось смещается на величину R . Точки касания тела с основанием неподвижны относительно последнего.
На практике всегда реализуется качение с проскальзыванием. Качение с проскальзыванием – контакт двух тел осуществляется по некоторой поверхности вследствие упругопластических и вязкопластических деформаций
Контакт реальных тел качения представляет собой площадку конечных размеров, а не точку или линию, тогда линия действия реакции F* n плоскости не совпадает с линией действия нормальной силы Fn. Точка ее приложения смещается от центра контактной площадки к ее передней границе.
Основные законы трения качения: 1. Момент сопротивления качению всегда направлен в сторону противоположную, тому направлению, в котором приложенные к телу силы стремятся его повернуть, или действительному повороту под действием этих сил (реактивный характер).
2. Момент сопротивления качению изменяется от нуля до своего максимального значения . Максимальный момент сопротивления качению пропорционален коэффициенту трения качения и силе нормального давления: .
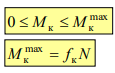
3. Коэффициент трения качения есть величина постоянная для данного вида и состояния соприкасающихся поверхностей (fк = const).
4. Момент сопротивления качению в широких пределах не зависит от радиуса катка.
Если коэффициент трения скольжения является безразмерной величиной, то коэффициент трения качения измеряется единицами длины и равен по величине указанному смещению равнодействующей нормального давления. В силу малости деформаций коэффициент трения качения имеет очень малую величину и составляет, например, для стального бандажа по стальному рельсу 0.0005 м.
11. Произвольная пространственная система сил.
Произвольная пространственная система сил - это система сил, векторы которых
произвольным образом размещены в пространстве.
Как показано в § 5.2, произвольная пространственная система сил сводится к главному вектору
и главногу моменту 
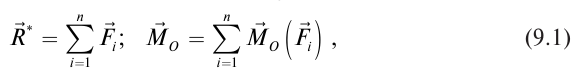
а также доказано, что для равновесия этой системы сил необходимо и достаточно, чтобы главный вектор и главный момент системы были равны нулю:
