Файл: Аксиома 2 аксиома эквивалентности системы сил.docx

В кинематике точки рассматриваются характеристики движения точки, такие, как скорость, ускорение, и методы их определения при различных способах задания движения. Важным в кинематике точки является понятие траектории. Траекторией точки называется геометрическое место ее последовательных положений в пространстве с течением времени относительно рассматриваемой системы отсчета.

По виду траекторий движения точки делятся на прямолинейные и криволинейные. Форма траектории зависит от выбранной системы отсчета. Одно и то же движение точки может быть прямолинейным относительно одной системы отсчета и криволинейным относительно другой. Например, если с летящего горизонтально Земле с постоянной скоростью самолета отцеплен груз, то, пренебрегая сопротивлением воздуха и учитывая только действие силы тяжести, получим в качестве траектории движения центра масс груза относительно самолета прямую линию, а относительно Земли — параболу.
19. Способы задания движения точки.

Рассмотрим три существующих способа задания движения материальной точки: координатный, векторный и естественный.

Чтобы иметь возможность определить параметры движения точки необходимо задать закон ее движения.

В зависимости от известных величин и поставленной задачи могут быть использованы следующие способы задания движения точки: векторный, координатный и естественный.

Векторный способ

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.

---

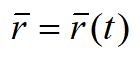
Координатный способ

При координатном способе задания движения задаются координаты точки как функции времени:

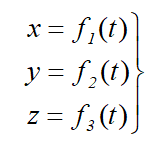Уравнения движения точки в координатной форме

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t.

Чтобы записать уравнение траектории движения материальной точки в явной форме, надо исключить из них параметр времени t.

Естественный способ

При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t).

Этим способом удобно пользоваться, если траектория точки заранее известна.

20. Скорость точки. Определение скорости точки при различных способах

задания движения.

Скоростью точки называют кинематическую меру ее движения, равную производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета.

Скорость относительно выбранной системы отсчета это одна из основных характеристик движения точки.

Вектор скорости направлен по касательной к траектории точки в сторону движения.

Рассмотрим перемещение точки за малый промежуток времени Δt:



тогда



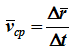
средняя скорость точки за промежуток времени Dt.

Скорость точки в данный момент времени

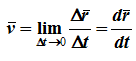
Скорость точки при векторном способе задания движения

Положение движущейся точки М относительно системы отсчета в момент времени t₁ определяется радиус-вектором r.

В другой момент времени t₁=t+Δt точка займет положение М₁ с радиус-вектором 

---

r₁.

За время Δt радиус-вектор движущейся точки изменится на



Средней скоростью v_ср называется отношение изменения радиус-вектора Δr к изменению времени Δt.



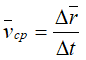
Скорость точки равна первой производной по времени от ее радиус-вектора.

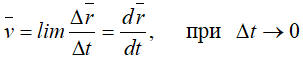
Скорость точки при координатном способе задания движения

Разложим радиус-вектор и скорость на составляющие, параллельные осям координат. Получим



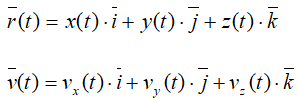
После дифференцирования



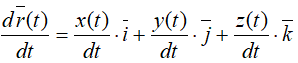
Отсюда следует



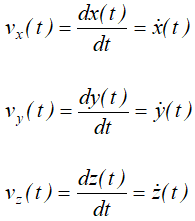
Проекция скорости точки на какую-либо координатную ось равна первой производной по времени от соответствующей координаты этой точки.

Модуль скорости и направляющие косинусы равны:



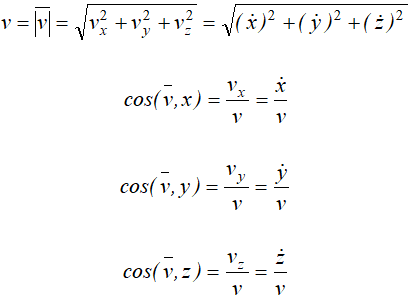
Если точка движется в плоскости, то, выбрав оси координат Ox и Oy в этой плоскости, получим:



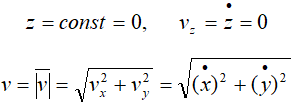
Для прямолинейного движения точки координатную ось, например ось Ox, направляем по траектории. Тогда

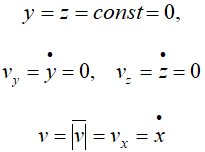
Скорость точки при естественном способе задания движения

Пусть скорость точки задана естественным способом

---

, т.е. заданы траектория точки и закон ее движения по траектории s=f(t).



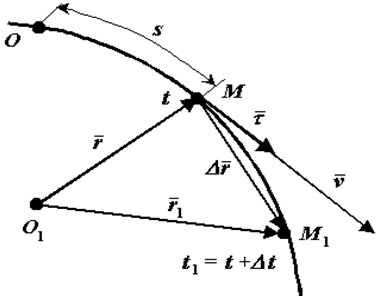
Рис. 2

Вычислим скорость точки. Используем радиус-вектор r. движущейся точки, начало которого находится в неподвижной точке O₁




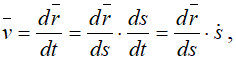
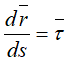
— единичный вектор, направленный по касательной к траектории в сторону возрастающих расстояний.



При ds>0 направления векторов τ и dr совпадают.

Если точка движется в сторону убывающих расстояний, то ds<0 и направления векторов τ и dr противоположны.

При

вектор скорости направлен по τ, т.е. в сторону возрастающих расстояний;

при

он имеет направление, противоположное τ, т.е. в сторону убывающих расстояний.


— алгебраическая скорость точки, проекция скорости v на положительное направление касательной к траектории.

Естественное задание движения точки полностью определяет скорость по величине и направлению.

21. Ускорение точки. Определение ускорения точки при различных

способах задания движения.

Ускорением точки называют меру изменения ее скорости, равную производной по времени от скорости этой точки или второй производной от радиус-вектора точки по времени.

Ускорение характеризует изменение вектора скорости по величине и направлению и направлено в сторону вогнутости траектории.

Среднее ускорение

---

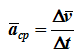
характеризует изменение вектора скорости за малый промежуток времени
Δt.

Ускорение точки в данный момент времени



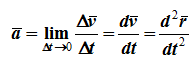
При координатном способе задания движения точки вектор ускорения определяют через его проекции на оси координат, которые равны вторым производным от соответствующих координат по времени:

 ,   ,   . (1.9)

 Если известны проекции ускорения на оси координат, то модуль вектора ускорения и его направляющие косинусы находят по формулам:

, (1.10)

где   – углы между вектором ускорения и осями координат.

При естественном способе задания движения с движущейся точкой связывают естественную систему координат (рис. 1.5). Естественный трехгранник составляется из трех пересекающихся взаимно перпендикулярных плоскостей: 1 – соприкасающейся, 2 – нормальной и 3 – спрямляющей. Линии пересечения плоскостей образуют правую систему естественных осей координат: τ, n и b, определяемых единичными векторами   , которые называют единичными векторами касательной, главной нормали и бинормали соответственно.

 Вектор ускорения точки в естественной системе определяют по формулам: 

---