где М — средняя арифметическая простая;

ΣV— сумма вариант;

n — число наблюдений.

Предположим, что длительность случаев временной нетрудоспособности при гриппе у 6 рабочих была 3, 4, 5, 8, 7, 9 дней. Средняя длительность одного случая составила:

Алгебраически это можно выразить так:

Для сгруппированного вариационного ряда вычисляют среднюю арифметическую взвешенную. Формула ее вычисления:


где М — средняя арифметическая взвешенная;

ΣVp — сумма произведений вариант на их частоты;

n — число наблюдений.

Поскольку в сгруппированных вариационных рядах отдельные варианты встречаются с разной частотой (т. е. имеют разный удельный вес), что отражается на результате средней величины, и данное влияние прямо пропорционально числу повторений вариант, то эта средняя арифметическая и получила название взвешенной.

Возвращаясь к нашему примеру (табл. 1), чтобы узнать средний возраст больных с инфарктом миокарда, необходимо определить сумму лет всех 30 больных. С этой целью каждая варианта умножается на ее частоту, а затем произведения суммируются. Деление данной суммы на общее количество больных позволяет установить средний возраст. Расчеты представлены следующим образом:

В развернутом виде алгебраически расчеты средней взвешенной будут выглядеть так:

M=49.3 (лет)
Методика расчета средней взвешенной приводится в табл. 2 (способ I).

Как уже указывалось, при малом числе наблюдений размер средней арифметической может оказаться неточной, случайной величиной, т. е. не отражать общую количественную закономерность изучаемых явлений. Значение средней арифметической значительно ближе к истинной характеристике и имеет большую степень точности в оценке

---

изучаемой закономерности при большом числе наблюдений. Это не означает, однако, что при малом числе наблюдений количественной закономерности установить нельзя. Методы статистики позволяют и на основании небольшого числа исследований выявить с определенной степенью достоверности средние характеристики изучаемого явления.
Таблица 2

Расчеты по определению средней величины и среднеквадратичного отклонения

для сгруппированного вариационного ряда

(I—обычный способ, II—способ моментов)

Возраст больного V	Число больных, Р	I способ							II способ
		Vp	D=V-M	dp			d2	d2р	d=V-A	Dp			d2	d2р
39	1	39	-10,3	-10,3		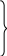-72,9	105,09	103,09	-9,0	-9,0		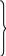-56,0	81,0	81,0
41	1	41	-8,3	-8,3			68,89	68,89	-7,0	-7,0			49,0	49,0
42	4	168	-7,3	-29,2			53,29	213,16	-6,0	-24,0			36,0	144,0
43	2	86	-6,3	-12,3			39,69	79,38	-5,0	-10,0			25,0	50,0
46	3	138	-3,3	-9,9			10,89	32,67	-2,0	-6,0			4,0	12,0
48	2	96	-1,3	-2,6			1,69	3,38	0,0	0,0			0,0	0,0
50	4	200	0,7	2,8			0,49	1,96	2,0	8,0			4,0	16,0
52	3	156	2,7	8,1		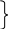+72,9	7,29	24,81	4,0	12,0		+95,0	16,0	48,0
54	5	270	4,7	23,5			22,09	110,45	6,0	30,0			36,0	180,0
56	4	224	6,7	26,8			44,89	179,56	8,0	32,0			64,0	256,0
61	1	61	11,7	11,7			136,89	136,89	13,0	13,0			169,0	169,0
n=30 ΣVp=1479				Σdp=0			Σd2 =954.3			Σdp=39			Σd2 p=1005

---

Средняя арифметическая имеет следующие свойства:

1. 
   сумма отклонений от средней равна нулю (см. табл. 2, гр. 5);
   
2. 
   при умножении (делении) всех вариант на один и тот же множитель (делитель) средняя арифметическая умножается (делится) на тот же множитель (делитель);
   
3. 
   если прибавить (вычесть) ко всем вариантам одно и то же число, средняя арифметическая увеличивается (уменьшается) на то же число.
   

Эти свойства могут быть использованы для облегчения и упрощения расчета средней арифметической.

Первое свойство, например, служит обоснованием для расчета средней арифметической по способу моментов.

Как видно из табл. 2 (гр. 5), сумма всех отклонений вариант от средней равна нулю (отклонение d — это разность между каждой вариантой и средней величиной, т. е. d = V-M). Поскольку в сгруппированном вариационном ряду варианты имеют различную частоту, то каждая из них в итоге дает отклонения, зависящие от этой повторяемости. Следовательно, значение отклонения варианты необходимо умножить на частоту, а затем суммировать все эти произведения. Каждая варианта отклоняется от средней величины в большую или меньшую сторону со знаком «+» или «-». Эти значения следует учитывать при проведении вычислений. Сумма отрицательных отклонений равна -72,9, сумма положительных отклонений составляет 72,9, а итоговая сумма всех отклонений равна нулю (Σdp = 0). Это свидетельствует о том, что средняя величина действительно есть общая количественная характеристика данного вариационного ряда, так как она взаимоисключает, взаимоуничтожает все отклонения. Это свойство положено в основу вычисления средней величины по способу моментов. Значение средней определяется по формуле , где А является условной средней величиной. Если А является истинной средней, т. е. А = М, то сумма ее отклонений будет равна нулю, если же она не является истинной средней, то сумма отклонений будет иметь значение, отличное от нуля, и явится основой для определения поправки. В табл. 2 (II способ) показаны этапы вычис­ления средней величины по способу моментов (А = 48). Из гр. 9 табл. 2

---

видно, что сумма отклонений Σdp равна 39. С учетом поправки легко определить действительное значение средней величины, подставив соответствующие значения в формулу:



Таким образом, полученное значение средней арифметической величины по способу моментов идентично таковому, найденному обычным способом.

При выборе условной средней А следует ориентироваться на моду или медиану.

Способ моментов значительно упрощает расчеты и делает их более быстрыми.

Второе свойство средней арифметической полезно применять при анализе вариационного ряда, состоящего либо из очень больших, либо из очень малых величин. Имеются, например, варианты: 0,0001; 0,0002; 0,0003. Используя это свойство, увеличим их в 10000 раз. Получим величины 1, 2, 3. Средняя арифметическая из них равна 2, а искомая средняя арифметическая в 10000 раз меньше, т. е. 0,0002.

При обработке вариационного ряда, состоящего их положительных и отрицательных значений, иногда бывает полезно прибавить ко всем вариантам такое число, чтобы сделать их все положительными. Из полученного среднего результата эту величину следует вычесть. Например, имеются величины: +10, +5, -3, -1, +6, -1, -2. Определим среднюю арифметическую:



Чтобы избавиться от отрицательных величин, можно использовать третье свойство средней арифметической, т. е. прибавить к каждой варианте определенное число, например, в нашем случае 4. Тогда величины приобретут следующий вид: 14, 9, 1, 3, 10, 3, 2. Их сумма равна 42. При делении на 7 получим 6. При вычитании 4 из 6 получим среднюю арифметическую величину 2.

---

МЕТОДЫ ОЦЕНКИ КОЛЕБЛЕМОСТИ РЯДА

И ТИПИЧНОСТИ СРЕДНИХ ВЕЛИЧИН
Средние арифметические величины, взятые сами по себе без учета колеблемости рядов, из которых они вычислены, имеют подчас ограниченное значение. Средние — это величины, вокруг которых рассеяны различные варианты, поэтому понятно, что чем ближе друг к другу отдельные варианты по своей количественной характеристике, тем меньше рассеяние, колеблемость ряда, тем типичнее его средняя. Одинаковые по размеру средние могут быть получены из рядов с различной степенью рассеяния.

Приблизительно о колеблемости можно судить по амплитуде (размаху) вариационного ряда — разности максимальной и минималь­ной вариант. Символика обозначения амплитуды: Am = Vmax-Vmin.

Основной, общепринятой мерой колеблемости вариационного ряда является среднее квадратическое отклонение, обозначаемое греческой буквой σ (сигма малая).

Чем больше среднее квадратическое отклонение, тем, следовательно, степень колеблемости данного ряда выше. Так, при определении средней длительности послеоперационного лечения аппендицита в двух больницах были получены следующие результаты:

Больница 1	Больница 2
М=9 дней	М=9 дней
σ =±2 дня	σ =±4 дня

Средняя длительность лечения в обеих больницах одинакова. Однако в первой больнице сроки послеоперационного лечения у отдельных больных были близки к 9 дням. Во второй больнице колебания были значительнее, отсюда и среднеквадратическое отклонение здесь больше, и следовательно, полученная средняя величина послеоперационного периода является менее типичной, чем в первой больнице.

Среднее квадратическое отклонение характеризует среднее отклонение всех вариант вариационного ряда от средней арифметической величины. Поскольку отклонения вариант от средней, как было сказано выше, имеют значения с «+» и «-», то при суммировании они взаимоуничтожаются. Чтобы избежать этого, отклонения возводятся во вторую степень, а затем, после определенных вычислений, производится обратное действие — извлечение корня квадратного. Поэтому среднее отклонение именуется квадратическим.

---

Смотрите также файлы

• Газ анализаторы газды баылау шін олданылады.docx

• Практическоезадание 5.docx

• График проведения Класс Предмет Дата проведения 6 а, история.docx

• .docx

• 2344402 629003, Россия, ЯмалоНенецкий ао, г.docx