Расчеты по определению доверительных границ в этом случае выглядят следующим образом:

М±2m=49.3±2*1.0=49.3±2.0=47.3-51.3 (лет)
ПРИМЕЧАНИЕ: В руководствах по санитарной статистике средняя величина генеральной совокупности обозначается , а выборочной –

ПОНЯТИЕ О РАСПРЕДЕЛЕНИИ ПРИЗНАКА

---

В СТАТИСТИЧЕСКОЙ СОВОКУПНОСТИ
Элементы, составляющие статистическую совокупность, имеют различные по величине значения изучаемого признака, и каждое из этих значений встречается в группе с неодинаковой частотой. Зависимость между значением величины признака и частотой, с которой оно встречается, называется характером распределения признака. Его можно определить только на достаточно большой совокупности наблюдений. Изучая характер распределения признака, получают важную информацию о закономерностях, присущих тому или иному явлению, а также возможность правильно выбрать статистические критерии для анализа и обобщения.


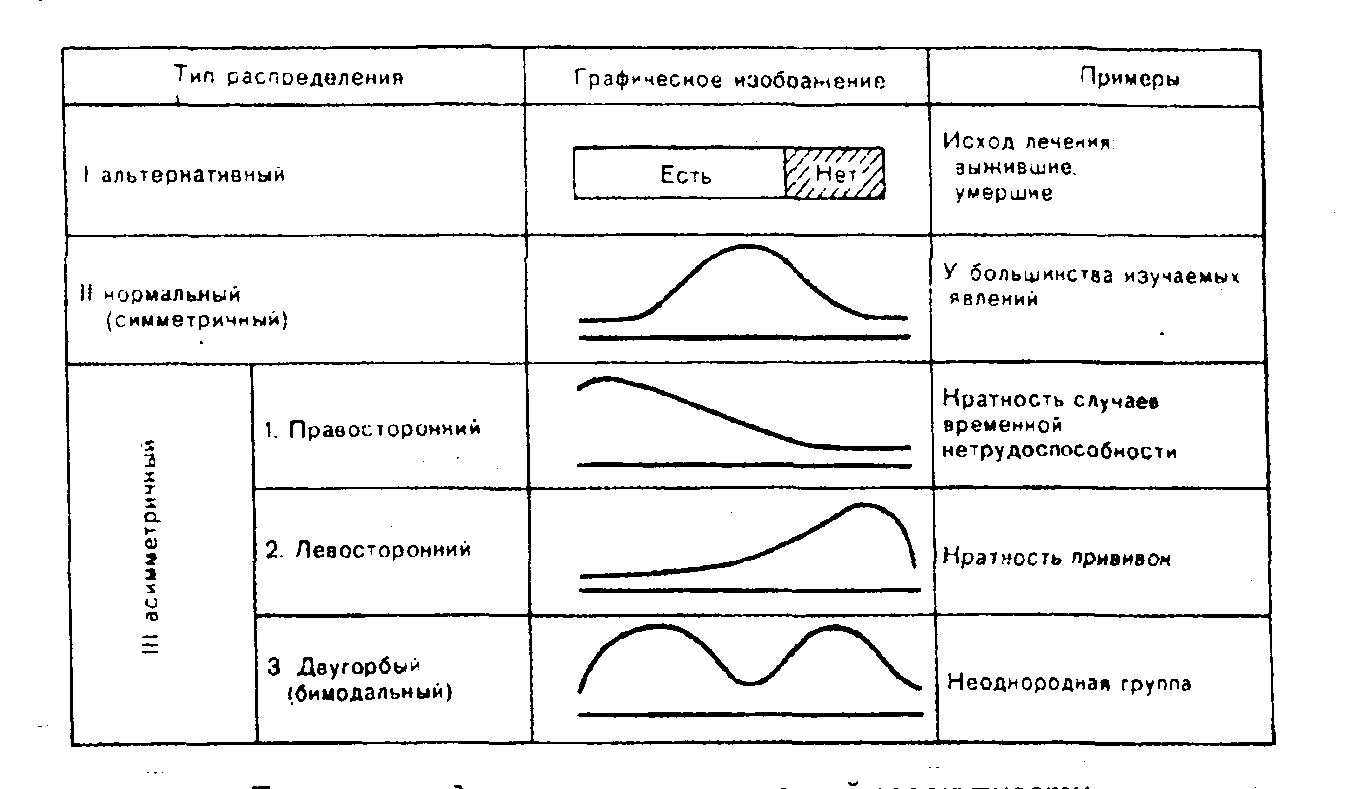
Типы распределения статистической совокупности
В медицинских исследованиях встречаются разные по характеру распределения: альтернативный, нормальный (симметричный), асимметричный (правосторонний, левосторонний, двугорбый — бимодальный) и др. На рисунке показаны основные типы распределения статистической совокупности.

Чаще других типов встречается нормальное распределение, которое в статистике называют еще распределением Гаусса. Оно характеризуется не только симметричностью, но также «ниспадающими» концами кривой распределения. При таком распределении признака в вариационном ряду мода, медиана и средняя арифметическая практически совпадают по значению. Нормальный характер распределения обычно наблюдается в рядах, вариантами которых являются количественные признаки: рост, масса тела, уровень артериального давления, сроки госпитализации и др. Следует также отметить, что с помощью критерия Стьюдента t можно сравнивать вариационные ряды именно с нормальным характером распределения признака.
ОПРЕДЕЛЕНИЕ ДОСТОВЕРНОСТИ РАЗЛИЧИЙ

СРЕДНИХ ВЕЛИЧИН
В научно-исследовательской практике часто бывает необходимо сравнение двух средних арифметических величин, например, при сравнении результатов в контрольной и экспериментальной группах, при

---

сравнении показателей здоровья населения в различных местностях за различные годы и т. д.

Применяемый метод оценки достоверности средних величин позволяет установить, насколько выявленные различия существенны, то есть носят ли они достоверный характер или являются результатом действия случайных причин.

В основе метода лежит определение так называемого критерия Стьюдента t (коэффициента достоверности). Величина его определяется отношением разности сравниваемых средних величин к ошибке их разности. Ошибка разности равна корню квадратному из суммы квадратов средних ошибок сравниваемых величин .

Таким образом, коэффициент достоверности определяется по формуле:



2 где М₁ — средняя величина первого исследования;

М₂ — средняя величина второго исследования;

m₁ и m₂ — ошибки репрезентативности сравниваемых средних величин.

Критерий достоверности t указывает, во сколько раз разность сравниваемых средних превышает их ошибку. При различных значе­ниях критерия существует определенная мера надежности, которая говорит о существенности, достоверности выявленных различий между сравниваемыми средними.

В медико-биологических исследованиях достаточно иметь значение t, равное или больше 2, тогда выявленные различия не случайны, достоверны, статистически подтверждены (с вероятностью более 95%). Если значение критерия меньше 2, то разница не доказана, носит случайный характер, статистически не подтверждается (вероятность менее 95%).

Пример. У 47 больных с хронической пневмонией с легочной недостаточностью I степени среднее количество циркулирующей крови M₁ составило 6,64 л (m₁ = ±0,17 л). В контрольной группе (56 человек)

---

эти показатели составили: М₂ = 6,12 л, m₂ = ± 0,13 л.

Разность среднего количества циркулирующей крови у больных хронической пневмонией I стадии и контрольной группы оказалась вполне убедительной:

При числе наблюдений в каждой группе менее 30 коэффициент достоверности необходимо каждый раз определять по таблице Стьюдента.
ОЦЕНКА ДОСТОВЕРНОСТИ РЕЗУЛЬТАТОВ

СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ

ПРИ ИСПОЛЬЗОВАНИИ ОТНОСИТЕЛЬНЫХ ПОКАЗАТЕЛЕЙ
Определение средней ошибки для относительных показателей производится по формуле:



где Р — величина относительного показателя;

q — величина, обратная Р и выраженная как (1-Р), (100-Р), (ЮОО-Р) и т. д., в зависимости от основания, на которое рассчитан показатель;

n — число наблюдений в выборочной совокупности (для числа наблюдений менее 30 берется n-1).

Зная средние ошибки относительных показателей, по аналогии со средними арифметическими величинами можно определять доверительные границы генеральной совокупности и использовать метод оценки достоверности разности этих показателей. При этом используется следующая формула.

Пример. В городе А со 135000 населения заболело гриппом 1600 человек, в городе Б с 68000 населения заболело 500 человек. Заболеваемость на 1000 человек в городе А составила 11,85, в городе Б — 7,35. Требуется определить, является ли преобладание заболеваемости гриппом в городе А случайным или оно определяется какими-то причинами, предположим, санитарно-эпидемиологического характера.

Находим средние ошибки показателей:



Определяем коэффициент достоверности:


Показатель достоверности значительно превышает значение t > 2, при котором разница признается достоверной. Следовательно, уровни

---

заболеваемости в городах А и Б носят неслучайный характер. Необходимо найти причины, способствующие более интенсивному распространению гриппа в городе А.

С ледовательно, для определения доверительных границ значения средней арифметической генеральной совокупности используют формулу: ,

а для относительных показателей эта формула имеет вид: .

,

Вопросы для самопроверки

1. 
   С какой целью используются в медицинских исследованиях средние величины и их параметры?
   
2. 
   Перечислите основные направления в медицинских и социально-гигиенических исследованиях, где широко используются средние величины.
   
3. 
   Дайте определение средней величины.
   
4. 
   Какие требования предъявляются при работе со средними величинами?
   
5. 
   Дайте определение вариационного ряда.
   
6. 
   Какие типы количественных вариаций различают?
   
7. 
   Какие учетные признаки можно использовать для построения вариационного ряда и расчета средней арифметической?
   
8. 
   Назовите основные элементы вариационного ряда.
   
9. 
   Как вычисляется средняя арифметическая простая?
   
10. 
    Как вычисляется средняя арифметическая взвешенная?
    
11. 
    Назовите основные свойства средней арифметической величины.
    
12. 
    Какие особенности лежат в основе расчетов средней арифметической величины по способу моментов?
    
13. 
    Что такое среднее квадратическое отклонение и его значение?
    
14. 
    Укажите особенности, на которых основано вычисление среднего квадратического отклонения по способу моментов.
    
15. 
    Роль коэффициента вариации и его применение.
    
16. 
    Понятие о достоверности полученных данных (ошибка репрезентативности).
    
17. 
    Чем определяется величина ошибки репрезентативности?
    
18. 
    Какова формула ошибки (т) для относительных показателей?
    
19. 
    Как определяются доверительные границы средней в генеральной совокупности и с какой целью?
    
20. 
    Как определяется достоверность различий средних величин, для каких целей?
    
21. 
    Как определяется достоверность различий относительных показателей?
    

Вариант 1

А. В районе

---

Смотрите также файлы

• Газ анализаторы газды баылау шін олданылады.docx

• Практическоезадание 5.docx

• График проведения Класс Предмет Дата проведения 6 а, история.docx

• .docx

• 2344402 629003, Россия, ЯмалоНенецкий ао, г.docx