Файл: Средние величины. Порядок составления и обработки вариационного ряда. Оценка достоверности результатов исследования.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 06.11.2023

Просмотров: 258

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


Среднее квадратическое отклонение определяют по формуле:



Ход вычислений при определении среднеквадратического отклонения следующий:

  1. возвести каждое отклонение dво вторую степень;

  2. умножить квадрат каждого отклонения d2на соответствующую частоту р;

  3. суммировать полученные произведения Σd2p ;

  4. разделить данную сумму на количество вариант, входящих в вариационный ряд n (при числе наблюдений менее 30 сумма делится на n-1);

  5. извлечь квадратный корень из полученного частного.





Расчеты представлены в табл. 2 (I способ). Подставив полученные значения в формулу, находим среднеквадратическое отклонение:



При вычислении среднеквадратического отклонения по способу моментов используется следующая формула:



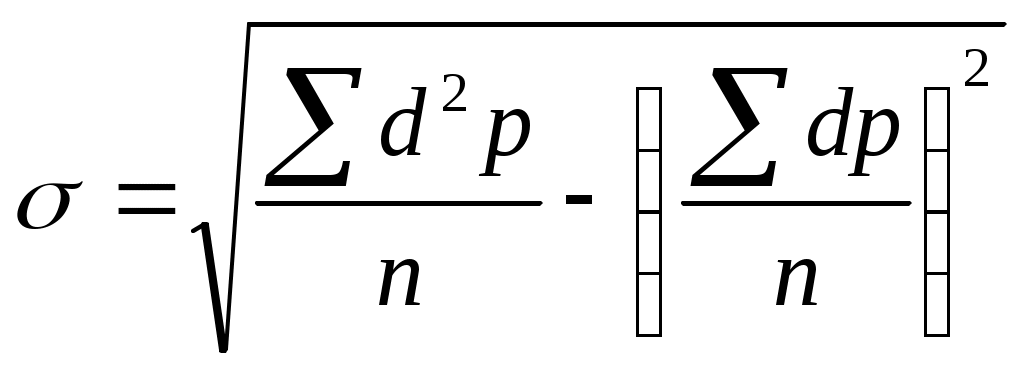
В чем суть этой формулы? Как видно, первая часть данного подкоренного выражения полностью идентична вышеприведенной формуле вычисления среднеквадратического отклонения обычным способом . Однако необходимо указать, что отклонения, находимые для условной средней А, заведомо будут ошибочными, т. е. отличными от отклонений, которые определяются для фактической средней М. Учитывая это обстоятельство, в формулу вносится поправ­ка, которая определяется для условной средней А. Эта поправка назы­вается моментом первой степени . Для разбираемого нами случая она равна + 1,3 (см. с. 11). Поскольку поправка вносится в подкоренное выражение, то она возводится во вторую степень.

Первая часть формулы называется моментом второй
степени, т. к. отклонение dвозведено во вторую степень.

Таким образом, формула вычисления среднеквадратического отклонения по способу моментов будет читаться как корень квадратный из разности момента второй степени и квадрата момента первой степени.

Определим среднеквадратическое отклонение по способу моментов для рассматриваемого нами примера (табл. 2). Подставив значения в формулу, находим:



Результаты вычисления среднеквадратического отклонения обычным способом и способом моментов идентичны. Однако, как указывалось выше, второй способ значительно убыстряет и упрощает расчеты.

Итак, нахождение среднеквадратического отклонения позволяет судить о характере однородности исследуемой группы наблюдений. Если величина среднеквадратического отклонения небольшая, то это свидетельствует о достаточно высокой однородности изучаемого явления. Среднюю арифметическую в таком случае следует признать вполне характерной для данного вариационного ряда. Однако слишком малая величина сигмы заставляет думать об искусственном подборе наблюдений. При очень большой сигме средняя арифметическая в меньшей степени характеризует вариационный ряд, что говорит о значительной вариабельности изучаемого признака или явления или о неоднородности исследуемой группы.

Оценка степени рассеяния вариант около средней может быть произведена с помощью коэффициента вариации, вычисляемого по формуле:



Значения коэффициента вариации С менее 10% свидетельствует о малом рассеянии, от 10 до 20% — о среднем, более 20% — о сильном рассеянии вариант вокруг средней арифметической.

Возвращаясь к нашему примеру (табл. 1 и 2), дадим характеристику изучаемому вариационному ряду.

Амплитуда этого вариационного ряда равна 22 годам (61-39 = 22),

σ =±5,64, .

Расчеты свидетельствуют о среднем рассеянии вариант, следовательно, средняя арифметическая величина вполне типична, а
исследуемая группа наблюдений является достаточно однородной.

Коэффициент вариации часто используется при оценке колеблемости рядов различных признаков, например, веса и роста. Непосредственное сравнение сигм в данном случае невозможно, т. к. среднеквадратическое отклонение — величина, именованная и выраженная абсолютным числом. Предположим, что при изучении физического развития группы подростков коэффициент изменчивости для веса составил 9,7%, а для роста — 4,6%. Эти цифры можно сравнить и сделать заключение, что в данном примере рост является более устойчивым признаком, чем вес.

Определение среднеквадратического отклонения представляет немалую ценность для медицинской науки и практики. При диагностике отдельных заболеваний очень важно оценить на основании конкретных исследований, какие признаки проявляются у соответствующей группы больных относительно одинаково, с небольшими колебаниями, а для каких признаков характерны большие индивидуальные колебания. Очень широко используется это свойство при оценке физического развития отдельных групп населения, при выработке стандартов школьной мебели и т. д.

Согласно теории вероятности в явлениях, подчиняющихся нормальному закону распределения, между значениями средней арифметической, среднеквадратического отклонения и вариантами существует строгая зависимость (правило трех сигм). Например, 68,3% значений варьирующего признака находятся в пределах М ± 1σ , 95,5% — в пределах М ± 2σ и 99,7% — в пределах М ± Зσ .

Данные, полученные эмпирически, не всегда строго совпадают с теоретическими, но они тем ближе к ним, чем больше число наблюдений и однороднее их состав.

Более подробно о применении правила трех сигм можно познакомиться в руководствах или пособиях по медицинской статистике.
ОПРЕДЕЛЕНИЕ ОШИБКИ РЕПРЕЗЕНТАТИВНОСТИ
Полученная средняя арифметическая М при повторных исследованиях под влиянием случайных явлений может колебаться на ту или иную величину. Это обусловлено тем, что исследуется, как правило, только часть изучаемых явлений, то есть выборочная совокупность. Сумма же всех единиц, представляющих изучаемое явление, называется генеральной совокупностью. Результаты, полученные на ос
нове выборочной совокупности, как правило, переносятся на генеральную совокупность. Чтобы определить степень точности выборочного наблюдения, необходимо оценить величину ошибки, которая может случайно произойти в процессе выборки. Такие ошибки носят название случайных ошибок репрезентативности т или средней ошибки средней арифметической. Они фактически являются разностью между средними числами, полученными при выборочном статистическом наблюдении, и аналогичными величинами, которые были бы получены при сплошном исследовании того же объекта (т. е. при исследовании генеральной совокупности).

Ошибки репрезентативности нельзя смешивать с ошибками регистрации или ошибками внимания (описки, просчеты, опечатки и др.), которые должны быть сведены до минимума.

Ошибки репрезентативности вытекают из самой сущности выборочного исследования. С помощью ошибок репрезентативности числовые характеристики выборочной совокупности распространяются на всю генеральную совокупность, то есть она характеризуется с учетом определенной погрешности.

Величины ошибок репрезентативности определяются как объемом выборки, так и разнообразием признака. Чем больше число наблюдений, тем меньше ошибка, чем больше изменчив признак, тем больше величина статистической ошибки.

На практике для определения средней ошибки выборки в статистических исследованиях пользуются следующей формулой:



где m — ошибка репрезентативности

σ — среднее квадратическое отклонение;

n — число наблюдений в выборке (при числе наблюдений менее 30 в подкоренное выражение вносится значение п-1).

Из формулы видно, что размер средней ошибки прямо пропорционален среднему квадратичному отклонению, т. е. вариабельности изучаемого признака, и обратно пропорционален корню квадратному из числа наблюдений.

Для рассматриваемого нами случая ошибка репрезентативности равна:


ОПРЕДЕЛЕНИЕ ДОВЕРИТЕЛЬНЫХ ГРАНИЦ
Определение величины ошибки репрезентативности необходимо для нахождения возможных значений генеральных параметров. Оценка генеральных параметров проводится в виде двух значений — минимального и максимального. Эти крайние значения возможных отклонении, в
пределах которых может колебаться искомая средняя величина генерального параметра, называются доверительными границами.

Согласно теории вероятностей можно предположить с достоверностью в 99,7%, что эти крайние значения отклонений будут не больше величины утроенной ошибки репрезентативности (М ± Зm); в 95,5% — не больше величины удвоенной средней ошибки средней величины (М ± 2m); в 68,3% — не больше величины одной средней ошибки (М±1m).

ПРИМЕЧАНИЕ. При малой выборке (менее 30) величину доверительного коэффициента необходимо определять каждый раз в зависимости от числа наблюдений по таблице Стьюдента.

Предположим, что с учетом аналогичных условий будут повторяться исследования на выявление среднего возраста больных с инфарктом миокарда, которое было взято нами в качестве примера, так как, естественно, количество больных инфарктом не замкнется количеством 30 человек. Можно ожидать, что полученные при этом средние, хотя бы и близкие по величине, все же будут отличаться друг от друга. Используя методику определения доверительных границ, нетрудно найти возможные колебания среднего возраста больных инфарктом миокарда. В медико-биологических исследованиях чаще всего используется 95% вероятность. Таким образом, с учетом двойной ошибки репрезентативности, если будут продолжаться исследования по определению среднего возраста больных инфарктом миокарда, можно определить, что средний возраст будет находиться в пределах следующих возрастных периодов: от 47,3 до 51,3 лет.

Таблица 3

Таблица значений критерия t (Стьюдента)


k (п-1)
Уровень вероятности, р

95%
99%
99,9%

1
12,7
63,6
636,6

2
4,3
9,9
31,6

3
3,1
5,8
12,9

4
2,7
4,6
8,6

5
2,5
4,0
6,8

6
2,4
3,7
5,9

7
2,3
3,5
5,4

8
2,3
3,3
5,1

9
2,2
3,2
4,7

10
2,2
3,1
4,6

11
2,2
3,1
4,4

12
2,2
3,0
4,3

13
2,1
3,0
4,2

14
2,1
2,9
4,1

15
2,1
2,9
4,0

16
2,1
2,9
4,0

17
2,1
2,8
3,9

18
2,1
2,8
3,9

19
2,0
2,8
3,8

20
2,0
2,8
3,8

21
2,0
2,8
3,8

22
2,0
2,8
3,7

23
2,0
2,8
3,7

24
2,0
2,7
3,7

25
2,0
2,7
3,7

26
2,0
2,7
3,7

27
2,0
2,7
3,6

28
2,0
2,7
3,6

29
2,0
2,7
3,6

30
2,0
2,7
3,6

∞
1.9
2.5
3.3

Смотрите также файлы