Файл: Курсовая работа Алгоритм быстрой сортировки студентка 3 курса 1 группы физикоматематического факультета.rtf
Добавлен: 06.11.2023
Просмотров: 189
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Глава 1. Основные теоретические аспекты алгоритма и сортировки
1.1 Понятие алгоритма и сортировки
1.2 Основные способы и алгоритмы сортировки массивов
1.4 Основные правила, понятия и теоремы
2.1 Описание алгоритма «быстрой сортировки»
2.2 Реализация на языке программирования
Глава 3. Анализ быстрой сортировки
3.1 Анализ наихудшего разбиения
В этой работе будет рассмотрена одна очень хорошая сортировка. Которая носит название быстрая сортировка, алгоритм которой признан наилучшим. Эта сортировка выполняются очень быстро.
Метод быстрой сортировки был разработан в 1960 году Ч.Ф.Р. Хоаром (C.A.R.Hoare) и он же дал ему это название. В настоящее время этот метод сортировки считается наилучшим. Он основан на использовании обменного метода сортировки. Это тем более удивительно, если учесть очень низкое быстродействие сортировки пузырьковым методом, который представляет собой простейшую версию обменной сортировки.
В основе быстрой сортировки лежит принцип разбиения. Сначала выбирается некоторое значение в качестве "основы" и затем весь массив разбивается на две части. Одну часть составляют все элементы, равные или большие "основы", а другую часть составляют все элементы меньшего значения, по которому делается разбиение. Этот процесс продолжается для оставшихся частей до тех пор, пока весь массив не будет отсортирован. Например, для массива " 7356821 " при использовании в качестве значения разбиения "5" будут получены следующие проходы при выполнении быстрой сортировки:
исходное состояние: 7356821;
первый проход: 2135687;
второй проход: 1235678.
Этот процесс продолжается для каждой части "2135" и "687". Фактически этот процесс имеет рекурсивную природу. И действительно, наиболее "аккуратно" быстрая сортировка реализуется посредством рекурсивного алгоритма.
Однако следует иметь в виду одно неприятное свойство быстрой сортировки. Если выбираемое для разбиения значение оказывается совпадающим с максимальным значением, то быстрая сортировка превращается в самую медленную с временем выполнения n. Однако на практике этот случай не встречается.
1.4 Основные правила, понятия и теоремы
Рекуррентные соотношения.
Для определения времени работы алгоритма, используются так называемые рекуррентные соотношения Получение рекуррентного соотношения для времени работы алгоритма, основанного на принципе "разделяй и властвуй", базируется на трех этапах.
Обозначим через T(n) время решения задачи, размер которой равен n. Если размер задачи достаточно мал, скажем, n≤с, где с – некоторая заранее известная константа, то задача решается непосредственно в течение определенного фиксированного времени
, которое мы обозначим через θ(1). Предположим, что наша задача делится на a подзадач, объем каждой из которых равен 1/b от объема исходной задачи. Если разбиение задачи на вспомогательные подзадачи происходит в течение времени D(n), а объединение решений подзадач в решение исходной задачи – в течение времени С(n), то мы получим такое рекуррентное соотношение:
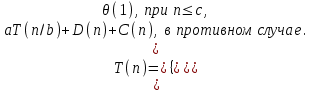
Основной метод решения рекуррентных отношений базируется на основной теореме, приведенной ниже.
Теорема 1.
Пусть
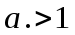 и
и 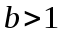 - константы,
- константы, 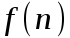 - произвольная функция, а
- произвольная функция, а 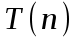 – произвольная функция, определенная на множестве неотрицательных целых чисел с помощью рекуррентного соотношения
– произвольная функция, определенная на множестве неотрицательных целых чисел с помощью рекуррентного соотношения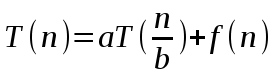 ,
,Тогда асимптотическое поведение функции
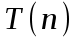 можно выразить следующим образом.
можно выразить следующим образом.1. Если
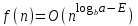 для некоторой константы
для некоторой константы 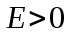 , то
, то 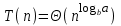 .
.2. Если
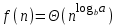 , то
, то 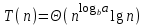 .
.3. Если
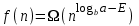 для некоторой константы
для некоторой константы 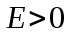 , и если
, и если 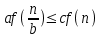 для некоторой константы
для некоторой константы 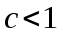 и всех достаточно больших n, то
и всех достаточно больших n, то 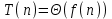 .
.Правило 1. Арифметическая прогрессия.
Сумма
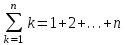
является арифметической прогрессией и ее значение равно:
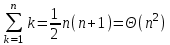 .
.Правило 2. Разбиение на части.
Можно разбить сумму на части и оценивать их по отдельности. В качестве примера возьмем сумму
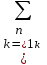 .Получим
.Получим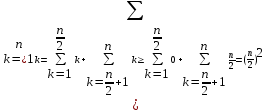 .
.1.5 Псевдокод
Перечислим основные соглашения, которые мы будем использовать.
-
Отступ от левого поля указывает на уровень вложенности. -
Циклы while, for, repeat и условные конструкции if, then, else имеют тот же смысл, что и в Паскале. -
Символ ► начинает комментарий (идущий до конца строки). -
Одновременное присваивание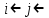
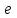 (переменные
(переменные 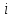 и
и 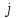 получают значение
получают значение 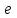 ) заменяет два присваивания
) заменяет два присваивания 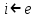 и
и 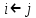 (в этом порядке).
(в этом порядке). -
Переменные локальны внутри процедуры (если не оговорено противное). -
Индекс массива пишется в квадратных скобках: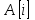 есть
есть 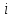 - й элемент в массиве
- й элемент в массиве 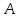 . Знак «..» выделяет часть массива:
. Знак «..» выделяет часть массива: 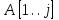 обозначает участок массива
обозначает участок массива 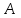 , включающий
, включающий 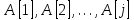 .
. -
Часто используются объекты, состоящие из нескольких полей, или, как говорят, имеющие несколько атрибутов. Значение поля записывается как имя_поля [имя_объекта]. Например, длина массива считается его атрибутам и обозначается length, так что длина массива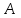 запишется как length
запишется как length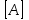 . Из контекста обычно ясно, что именно обозначают квадратные скобки (элемент массива или поле объекта).
. Из контекста обычно ясно, что именно обозначают квадратные скобки (элемент массива или поле объекта).
Переменная, обозначающая объект или массив, считается указателем на составляющие его данные. После присваивания

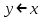 для любого поля
для любого поля 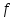 выполнено
выполнено 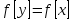 .
.-
Параметры передаются по значению: вызванная процедура получает собственную копию параметров; изменение параметра внутри процедуры снаружи невидимо. При передаче объектов копируется указатель на данные составляющие этот объект, а сами поля объекта – нет.
Глава 2. Реализация алгоритма «быстрой сортировки»
В этой главе мы рассмотрим сам алгоритм «быстрой сортировки» и процедуру разбиения массива на части. Также реализуем его на языке программирования.
2.1 Описание алгоритма «быстрой сортировки»
Быстрая сортировка (quicksort), как и сортировка слиянием, по своей природе рекурсивна, т.е. она для решения некоторой задачи вызывает саму себя для решения её подзадач; и основана на принципе «разделяй и властвуй». Сначала задача разбивается на несколько подзадач меньшего размера. Затем эти подзадачи решаются. И наконец, их решения комбинируются и получается решение исходной задачи.
Сортировка участка А [p..r] происходит так:
-
Элементы массива А переставляются так, чтобы любой из элементов А[р]…А[q] был не больше любого из элементов А [q+1]…A[r], где q — некоторое число в интервале р= -
Процедура сортировки рекурсивно вызывается для массивов A[p..q] и A[q+l..r].
После этого массив А [р...r] отсортирован.
Итак, процедура сортировки QUICKSORT выглядит следующим образом:
Quicksort (p,r)
-
если p -
то q←PART (p, r) -
Quicksort (p, q) -
Quicksort ( q+ 1, r)
Ключевой частью рассматриваемого алгоритма сортировки является функция Part, изменяющая порядок элементов массива А [р..r] без привлечения дополнительной памяти.
Выбираем элемент x=А [р] в качестве «граничного»; массив А [р..q] будет содержать элементы, не большие х. А массив A [q+l..r] — элементы, не меньшие х. Идея состоит в том, чтобы накапливать элементы, не большие х, в начальном отрезке массива A[p..i], а элементы, не меньшие х — в конце A[j..r]. В начале оба «накопителя» пусты: i = р-1, j = r + 1:
i ← p-1;
j ←r+1;
x ←A[p];
Создадим цикл, в котором найдем элементы виде A[j]<=x и A[i]>=x. Для этого мы будем уменьшать j пока A[j]<=x и увеличивать i пока A[i]>=x. Затем, сравнивая i и j, посмотри, где находятся наши элементы в массиве A[p..i] или в массиве A[j..r]. Затем проверим выполняется ли неравенство i
Хотя идея функции очень проста, сам алгоритм содержит ряд тонких моментов. Например, не очевидно, что индексы i и j не выходят за границы промежутка [р..r] в процессе работы. Другой пример: важно, что в качестве граничного значения выбирается А [р], а не, скажем, A[r]. В последнем случае может оказаться, что A[r] - самый большой элемент массива, и в конце выполнения процедуры будет i=j=r, так что возвращать j функции будет нельзя — нарушится требование q < r, и процедура Quicksort зациклится.
Время работы функции Part составляет
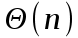 , где
, где 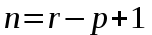 .
.2.2 Реализация на языке программирования
Мы рассмотрели алгоритм «быстрой сортировки», который описали на повседневном языке, понятном почти всем. А для реализации данного алгоритма был выбран язык программирования Pascal. Причина такого выбора заключается в том, что он был изначально разработан в учебных целях, прост и эффективен. Перевод программы на язык программирования подразумевает довольно глубокие знания того языка, на котором пишется программа. Вот еще одна причина, по которой был выбран язык Pascal.
Рассмотрим базовые процедуры и функции, которые использовались при написании программы.
Процедуры read и write используются для ввода и вывода данных.
Reset – процедура, открывающая файл для чтения.
Assign – процедура, предназначенная для связывания файловой переменной с файлом на диске.
Rewrite – процедура, открывающая файл для записи. Если файла не существует, то она создает его.
Close – процедура, закрывающая открытый файл.
Теперь мы рассмотрим более подробно структуру программы. В первую очередь назовем программу «Q123». Затем введем константу, которая определяет величину массива (в нашем случае n=10). Так же нам необходимо описать переменные и сам массив, которые будут использоваться в данной программе:
var
k:integer;
A:array [1..n] of integer;
Для ввода массива создадим специальный файл «input.txt», в который будем вводить сам массив. Например: 5 4 2 9 6 1 4 2 9 5.И файл, в который будем выводить отсортированный массив «output.txt».
assign (input,'input.txt'); reset (input);
assign (output,'output.txt'); rewrite (output);
С помощью оператора For прочтем массив из файла.
for k:=1 to n do read (A[k]);
Теперь мы опишем саму процедуру Quicksort, которая также будет включать свои переменные.
procedure QuickSort(p,r:integer);
var q:integer;
Эта переменная будет являться тем средним значением, которое мы получим в результате функции Part (ее опишем ниже). Затем процедура Quicksort вызывает саму себя уже для подмассивов [р..q] и [q+l..r].
Но это все будет выполняться, если будет выполняться условие p
if p
q:=Part(p,r);
QuickSort(p,q);
QuickSort(q+1,r);
end;
В этой процедуре используется функция Part, которая так же имеет свои переменные:
function Part(p,r:integer):integer;
var c,x,j,i,q:integer;