Файл: Курсовая работа Алгоритм быстрой сортировки студентка 3 курса 1 группы физикоматематического факультета.rtf
Добавлен: 06.11.2023
Просмотров: 182
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Глава 1. Основные теоретические аспекты алгоритма и сортировки
1.1 Понятие алгоритма и сортировки
1.2 Основные способы и алгоритмы сортировки массивов
1.4 Основные правила, понятия и теоремы
2.1 Описание алгоритма «быстрой сортировки»
2.2 Реализация на языке программирования
Глава 3. Анализ быстрой сортировки
3.1 Анализ наихудшего разбиения
Эта функция сортирует массив с помощью нескольких операторов. Но для начала нам необходимо ввести два накопителя, которые сразу пусты. И введем некоторое значение x.
i:=p-1;
j:=r+1;
x:=A[p];
С помощью оператора while мы будем повторять следующие действия.
while true do begin
И так, для начала мы будем уменьшать j, пока A[j]>=x:
repeat
j:=j-1
until A[j]<=x;
И увеличивать i , пока A[i]>=x:
repeat
i:=i+1
until A[i]>=x;
Проверим условие i
if (i
c:=A[i];
A[i]:=A[j];
A[j]:=c;
end
else break;
После этого мы присваиваем значение j самой функции Part.
В конце самой программы мы выводим отсортированный массив в раннее созданный файл «output.txt». Всю программу можно увидеть в приложении 1.
Глава 3. Анализ быстрой сортировки
Анализ алгоритма заключается в том, чтобы предсказать требуемые для его выполнения ресурсы. Иногда оценивается потребность в таких ресурсах, как память, пропускная способность сети или необходимое аппаратное обеспечение, но чаще всего определяется время вычисления. Путем анализа нескольких алгоритмов, предназначенных для решения одной и той же задачи, можно без труда выбрать наиболее эффективный. Но нам необходимо сделать анализ только одного алгоритма быстрой сортировки.
3.1 Анализ наихудшего разбиения
«Наиболее неравные части» получатся, если одна часть содержит n - 1 элемент, а вторая — всего 1. Предположим, что на каждом шаге происходит именно так. Поскольку функция разбиения занимает время
 , для времени работы
, для времени работы  получаем соотношение:
получаем соотношение: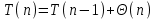 .
.Поскольку
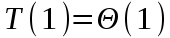 , имеем:
, имеем: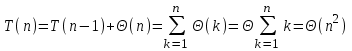
(последняя сумма - арифметическая прогрессия, см. правило 1). Дерево рекурсии для этого случая показано на рис. 1.

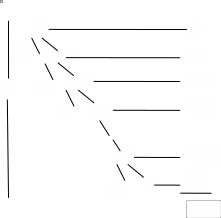
Рис.1
Мы видим, что при максимально несбалансированном разбиении время работы составляет
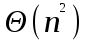 , как и для сортировки вставками. В частности, это происходит, если массив изначально отсортирован. Интуитивно видно, что этот случай является наихудшим. А теперь мы это строго докажем.
, как и для сортировки вставками. В частности, это происходит, если массив изначально отсортирован. Интуитивно видно, что этот случай является наихудшим. А теперь мы это строго докажем.
Для доказательства того, что время работы составляет
 , мы используем метод подстановки (смотри правило 3). Пусть
, мы используем метод подстановки (смотри правило 3). Пусть 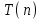 – наибольшее время работы алгоритма для массива длины n. Тогда, очевидно
– наибольшее время работы алгоритма для массива длины n. Тогда, очевидно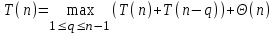 .
.В этой формуле мы рассмотрели все возможные разбиения на первом шаге. Предположим, что
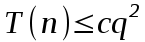 для некоторой константы с и для всех q, меньших не которого n. Тогда
для некоторой константы с и для всех q, меньших не которого n. Тогда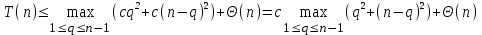 .
.Квадратный трёхчлен
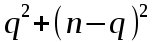 достигает максимума на отрезке
достигает максимума на отрезке 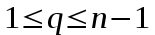 в его концах, т. к. вторая производная по q положительна и функция выпукла вниз. Этот максимум равен
в его концах, т. к. вторая производная по q положительна и функция выпукла вниз. Этот максимум равен 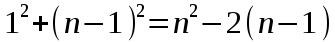 . Отсюда получаем
. Отсюда получаем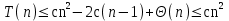 ,
,если константа с выбрана так, чтобы последнее слагаемое было меньше предпоследнего. Итак, время работы в худшем случае составляет
 .
.3.2 Наилучшее разбиение
алгоритм сортировка хоар программирование
Если на каждом шаге массив разбивается ровно пополам, быстрая сортировка требует значительно меньше времени. Действительно, в этом случае рекуррентное соотношение имеет вид
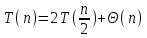
и, согласно теореме 1,
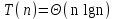

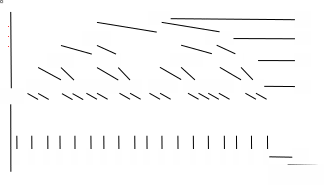
Рис.2
3.3 Промежуточный случай
Предположим, что среднее время работы (с точностью до множителя) совпадает со временем работы в наилучшем случае. Чтобы объяснить это, посмотрим, как меняется рекуррентное соотношение в зависимости, от степени сбалансированности разбиения.
Пусть, например, на каждом шаге массив разбивается на две части с отношением размеров 9:1. Тогда
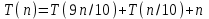
(для удобства мы заменили
 на
на 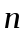 ). Дерево рекурсии показано на рисунке 3. На каждом уровне мы производим не более n действии, так что время работы определяется глубиной рекурсии.
). Дерево рекурсии показано на рисунке 3. На каждом уровне мы производим не более n действии, так что время работы определяется глубиной рекурсии.В данном случае эта глубина равна
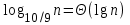 , так что время работы по-прежнему составляет Θ(nlgn), хотя константа и больше. Ясно, что для любого фиксированного отношения размеров частей (сколь бы велико оно ни было) глубина дерева рекурсии по-прежнему будет логарифмической, а время работы будет равно Θ(nlgn).
, так что время работы по-прежнему составляет Θ(nlgn), хотя константа и больше. Ясно, что для любого фиксированного отношения размеров частей (сколь бы велико оно ни было) глубина дерева рекурсии по-прежнему будет логарифмической, а время работы будет равно Θ(nlgn).

Рис. 3.
3.4 Вероятностные алгоритмы быстрой сортировки
Ранее мы предположили, что все перестановки входных значений равновероятны. Если это так, а размер массива достаточно велик, быстрая сортировка — один из наиболее эффективных алгоритмов. На практике, однако, это предположение не всегда оправдано.
Теперь мы введём понятие вероятностного алгоритма и рассмотрим два вероятностных алгоритма быстрой сортировки, которые позволяют отказаться от предположения о равной вероятности всех перестановок.
Идея состоит в привнесении случайности, обеспечивающем нужное распределение. Например, перед началом сортировки можно случайно переставить элементы, после чего уже все перестановки станут равновероятными (это можно сделать за время О (n)). Такая модификация не увеличивает существенно время работы, но теперь математическое ожидание времени работы не зависит от порядка элементов во входном массиве (они всё равно случайно переставляются).
Алгоритм называется вероятностным (randomized), если он использует генератор случайных чисел (random-number generator). Мы будем считать, что генератор случайных чисел Random работает так: RANDOM (a,b) возвращает с равной вероятностью любое целое число в интервале от а до b. Например. Random(0,1) возвращает 0 или 1 с вероятностью 1/2. При этом разные вызовы процедуры независимы в смысле теории вероятностей. Для такого вероятностного варианта алгоритма быстрой сортировки нет «неудобных входов»: т.к. количество перестановок, при которых время работы велико, совсем мало — поэтому вероятность того, что алгоритм будет работать долго невелика.
Аналогичный подход применим и в других ситуациях, когда в ходе выполнения алгоритма мы должны выбрать один из многих вариантов его продолжения, причём мы не знаем, какие из них хорошие, а какие плохие, но знаем, что хороших вариантов достаточно много. Нужно только, чтобы плохие выборы не разрушали достигнутого при предыдущих хороших.
Вместо того, чтобы предварительно переставлять элементы массива, мы можем внести элемент случайности в функцию Part. Именно, перед разбиением массива А [p..r] будем менять элемент А[р] со случайно выбранным элементом массива. Тогда каждый элемент с равной вероятностью может оказаться граничным, и в среднем разбиения будут получаться достаточно сбалансированными.
Этот подход заменяет разовую случайную перестановку входов в начале использованием случайных выборов на всём протяжении работы алгоритма. В сущности это то же самое, и оба алгоритма имеют математическое ожидание времени работы O(n lgn), но небольшие технические различия делают анализ нового варианта проще, и именно его мы будем рассматривать далее.
Изменения, которые нужно внести в процедуры, совсем неволики:
Rand-Part (А, р, г)
-
г <т- Random(р, г) -
поменять А[р] f-> A[i] -
return Partition (Л. р, г)
В основной процедуре теперь будет использоваться Randomized-Partition вместо Partition:
Randomized-Quicksort(A, р. г)
1 if р < г
2 then q *- Randomized-Partition( A, p, г)
-
Randomized-Quicksort( A. p, q) -
Randomized-Qijicksort( A, q + 1, r)
3.5 Нахождение и анализ среднего времени работы сортировки
3.5.1 Интуитивные соображения по нахождению среднего времени
Чтобы вопрос о среднем времени работы имел смысл, нужно уточнить, с какой частотой появляются различные входные значения. Как правило, предполагается, что все перестановки входных значений равновероятны.
Для наугад взятого массива разбиения вряд ли будут всё время происходить в одном и том же отношении — скорее всего, часть разбиений будет хорошо сбалансирована, а часть нет, примерно 80 процентов разбиений производятся в отношении не более 9:1.
Будем предполагать для простоты, что на каждом втором уровне все разбиения наихудшие, а на оставшейся половине уровней наилучшие (смотри рис. 4). Поскольку после каждого «хорошего» разбиения размер частей уменьшается вдвое, число «хороших» уровней равно Θ(lgn), а поскольку каждый второй уровень «хороший», общее число уровней равно Θ(lgn), а время работы — Θ(nlgn). Таким образом, плохие уровни не испортили асимптотику времени работы, а лишь увеличили константу, скрытую в асимптотическом обозначении.





Рис. 4. Два уровня плохой (n разбивается на n-1 и 1) и хороший (n-1 разбивается на две равные части).
3.5.2 Анализ среднего времени работы
Анализ разбиений.
Напомним, что перед тем как в функции Rand-Part вызывается функция Part, элемент А[р] переставляется со случайно выбранным элементом массива А [p..r]. Для простоты мы будем предполагать, что все числа в массиве различны. Хотя оценка среднего времени сохраняется и в том случае, когда в массиве есть одинаковые элементы, получить ее сложнее, и мы этого делать не будем.
Прежде всего, заметим, что значение q, которое возвратит функция Part, зависит только от того, сколько в массиве элементов, не больших x= А[р]. Число таких элементов мы будем называть рангом элемента x и обозначать rank(x). Если n число элементов массива, то, поскольку все элементы имеют равные шансы попасть на место А[р], все значения rank(x), от 1 до n, равновероятны и имеют вероятность 1/n.
Если rank(x)>1. то, как легко видеть, при разбиении левая часть будет содержать rank(x)-1 элементов – в ней окажутся все элементы, меньше x. Если же rank(x)=1, то левая часть будет содержать один элемент. Отсюда следует, что с вероятностью 1/n левая часть будет содержать 2,3,…,n-1 элементов, а с вероятностью 2/n – один элемент.
Рекуррентное соотношение для среднего времени работы.
Обозначим среднее время работы алгоритма Rand-Part для массива из n элементов через
 . Ясно, что
. Ясно, что  . Время работы состоит из времени работы функции Part, которое составляет
. Время работы состоит из времени работы функции Part, которое составляет  , и времени работы для двух массивов размеров
, и времени работы для двух массивов размеров 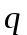 и
и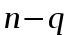 , причем
, причем 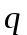 с вероятностью 2/n принимает значения 1 и с вероятностью 1/n значения 2, 3,…,n-1. Поэтому
с вероятностью 2/n принимает значения 1 и с вероятностью 1/n значения 2, 3,…,n-1. Поэтому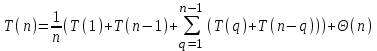
(1)
Слагаемое, соответствующее q=1, входит дважды и поскольку
 и
и 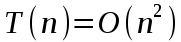 , имеем
, имеем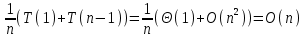 .
.Поэтому слагаемые