Файл: Курсовая работа Алгоритм быстрой сортировки студентка 3 курса 1 группы физикоматематического факультета.rtf
Добавлен: 06.11.2023
Просмотров: 175
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Глава 1. Основные теоретические аспекты алгоритма и сортировки
1.1 Понятие алгоритма и сортировки
1.2 Основные способы и алгоритмы сортировки массивов
1.4 Основные правила, понятия и теоремы
2.1 Описание алгоритма «быстрой сортировки»
2.2 Реализация на языке программирования
Глава 3. Анализ быстрой сортировки
3.1 Анализ наихудшего разбиения
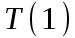и 
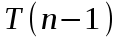в первой скобке (1) можно включить в 
. С учетом этого получаем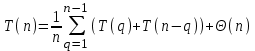
.Поскольку каждое слагаемое
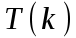, где k=1, 2,…,n-1, встречается в сумме дважды, ее можно переписать так: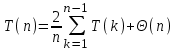
(2)
.
Решение рекуррентного соотношения.
Соотношение 2 можно решить, используя метод подстановки. Предположим, что
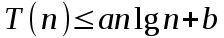, где константы 
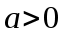и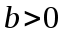 
пока неизвестны, и попытаемся доказать это по индукции. При n=1 это верно, если взять достаточно большие а и b. При n>1 имеем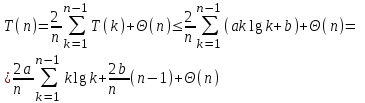
Ниже мы покажем, что первую сумму можно оценить так:
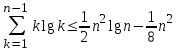
(3)
Используя это, получим
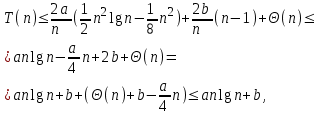
Если выбрать а так, чтобы аn/4 было больше
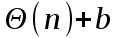. Следовательно, среднее время работы есть 
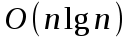.Доказательство оценки для суммы.
Нам осталось доказать оценку (3). Поскольку каждое слагаемое не превышает nlgn, получаем оценку
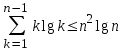.Для наших целей она не подходит – нам необходимо более точная оценка
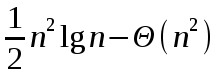.Если, заменив лишь
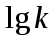на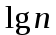 
, мы, оставив k в неприкосновенности, получим оценку
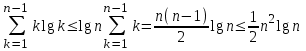.Осталось лишь заметить, что заменяя
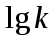на 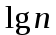, мы прибавили, по крайней мере по k к каждому слагаемом первой половины суммы (где k
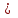n/2), всего примерно 
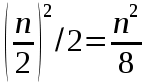.Более подробно,
.
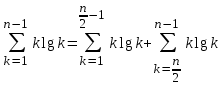
При
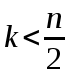имеем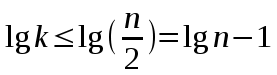 
. Поэтому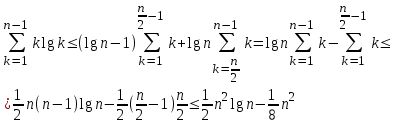
При n
2. Оценка (3) доказана.