Министерство науки и образования Российской Федерации Федеральное государственное образование бюджетное учреждение Высшего образования ТАМБОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра: «Механика и инженерная графика» Предмет: «Детали машин»

Контрольная работа №3 «Расчет второй ступени привода вертикального вала цепного конвейера цилиндрической зубчатой передачи»

Вариант 1-7 «А»

Выполнил: студент группы БХП-213 Воробьёва Софья Сергеевна

Проверил: профессор Родионов Юрий Викторович

Тамбов 2023



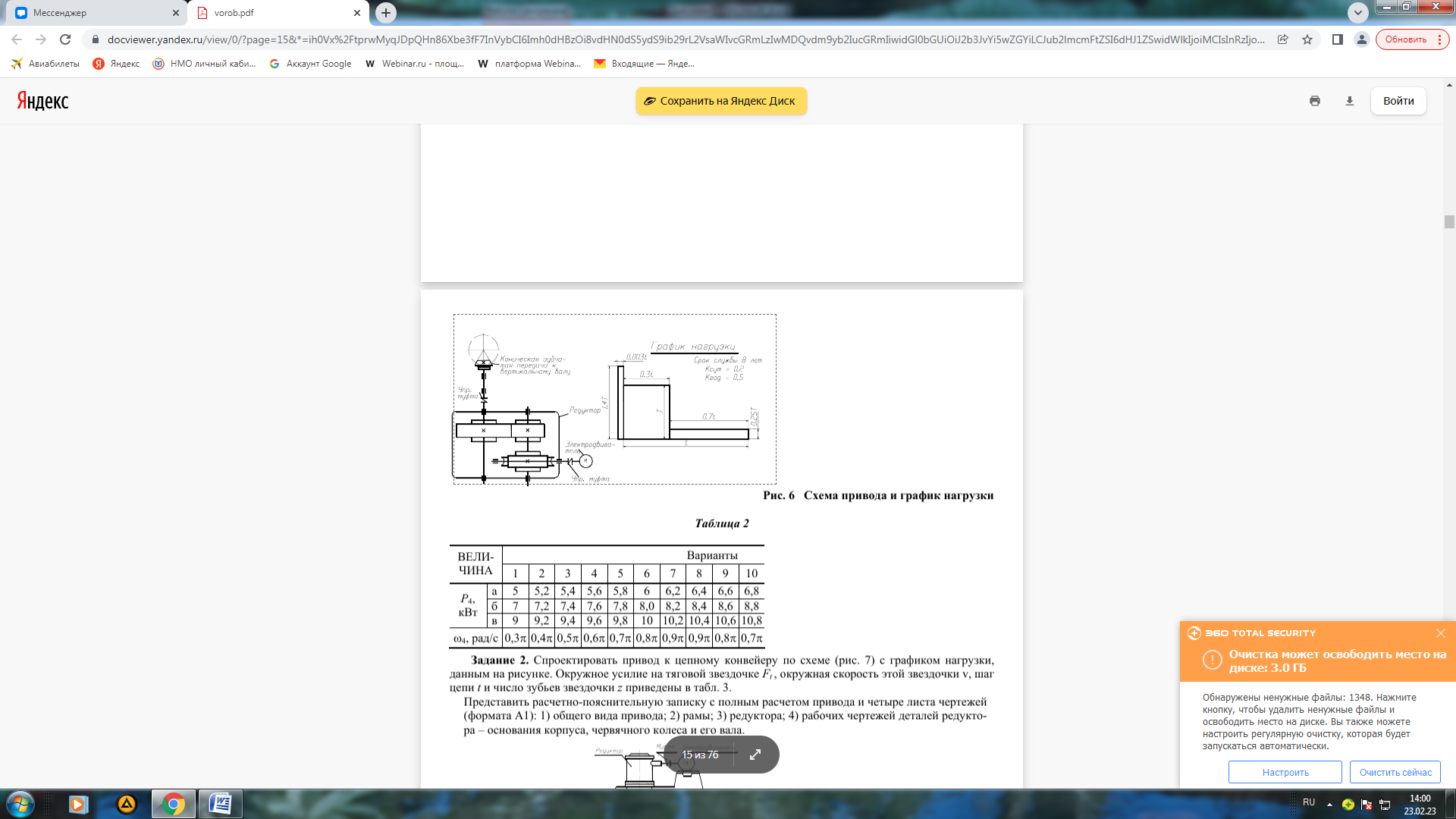
2. Расчет косозубой цилиндрической пары (в соответствии с ГОСТ 21354-87)

2.1 Выбор материалов для колес.

Свойства материалов Звенья передачи

Шестерня(1) Колесо(3)

Марка стали Сталь 45 Сталь 35

Термообработка Улучшение Нормализация

Предел прочности ϭ_В1 = 850 МПа ϭ_В2 = 550 МПа

Предел текучести ϭ_Т1 = 580 МПа ϭ_Т1 = 270 МПа

Твердость сердцевины 241…285 НВ 173…187 НВ

2.2 Определяем контактные напряжения по формуле:

[ϭ_H] = 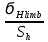K_HL,

Где 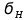limb = 2HB + 70

для шестерни:

HB = 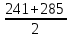= 263 HB

Ϭ_H01 = 2 * HB1 + 70 = 2 * 263 + 70 = 596 МПа

для колеса:

HB2 = 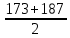= 180 HB

Ϭ_H02 = 2 * HB2 + 70 = 2 * 180 + 70 = 430 МПа

N_HE = 60c 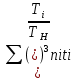= 60 * 1 ( 1³ * 27 * 8 * 365 * 0,5 * 24 * 0,2 * 0,3 + 0,25³ * 27 * 8 * 365 * 0,5 * 24 * 0,2 * 0,7) = 3,5 * 10⁶

N_HE > 1 * 10⁷ . K_HL = 1

Тогда допускаемые напряжения:

для шестерни:

[ϭ_Н1] = 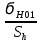K_HL = 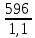* 1 = 542 МПа

для колеса:

[ϭ_Н2] = 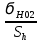K_HL = 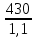* 1 = 391 МПа

для зубчатой передачи:

[ϭ_Н] =

---

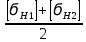
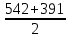= = 466,5 МПа

Проверим опасность нагрузки [1] слабого звена по условию:

[ϭ_Н] = 466,5 МПа ≤ 1,25 * 391 = 488,8 МПа

Перегруза колеса нет.

2.3 Определим [1] допускаемые напряжения изгиба, используя формулу:

[ϭ_F] = 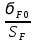K_FSK_FL

для шестерни:

Ϭ_F01 = 1,8 * HB1 = 1,8 * 263 = 473,4 МПа

для колеса:

Ϭ_F02 = 1,8 * HB2 = 1,8 * 180 = 324 МПа

для шестерни:

[ϭ_F1] = 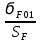K_FSK_FL = 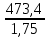* 1 * 1 = 271 МПа

для колеса:

[ϭ_F2] = 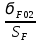K_FSK_FL = 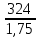* 1 * 1 = 185 МПа

2.4 Определяем [1] допускаемые напряжения при перегрузках:

для колеса по контактным напряжениям

[ϭ_H]max2 = 2,8 * ϭ_T2 = 2,8 * 270 = 756 МПа

для шестерни и колеса по изгибающим напряжениям

[ϭ_F]max1 = 0,8 * ϭ_T1 = 0,8 * 580 = 464 МПа

[ϭ_F]max2 = 0,8 * ϭ_T2 = 0,8 * 270 = 216 МПа

2.5 Определяем [1] вращающие моменты на колесе и на шестерне:

вращающий момент на колесе

Т₃ = 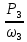= = 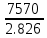2676,3 Н * м

вращающий момент на шестерне

Т₂ = 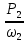= = 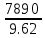819,96 Н * м

2.6 Определим диаметр шестерни [1]

d₁ = K_d 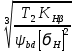* 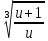= 680 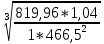* 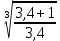= 116,8 мм

Предварительно принимаем d₁ = 118 мм

2.7 Рассчитываем геометрические параметры колес:

рабочая ширина колеса

b_ω = ψ_bd * d₁ = 1 * 118 = 118 мм

торцевой модуль

m_t = 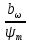= = 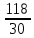3,9 мм

принимаем m_n = 4 мм

Угол наклона зубьев найдем из условия обеспечения плавности:

---

sinβ = 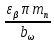= = 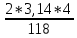0,2; β = 13º1'

Уточняем величину торцевого модуля

m_t = 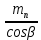= = 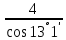4,1 мм

Число зубьев шестерни

z₁ = 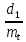= = 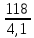28,78

Принимаем z₁ = 29 > z_min = 17.

Тогда число зубьев колеса z₂ = z₁u = 27 * 3,4 = 96,8

Принимаем z₂ = 99

Уточняем размеры диаметров делительных окружностей

d₁ = m_t * z₁ = 4,1 * 29 = 118,9 мм

d₂ = m_t * z₂ = 4,1 * 99 = 405,9 мм

и межосевого расстояния

a_ω = 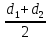= = 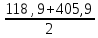262,4 мм

Принимаем a_ω = 263 мм и определяем окончательные геометрические параметры:

шестерни

d_ω1 = d₁ = 118,9 мм

d_a1 = d₁ + 2m_n = 118,9 + 2 * 4 = 126,9 мм

d_f1 = d₁ – 2,5m_n = 118,9 – 2,5 * 4 = 108,9 мм

b_ω1 = b_ω + 4 = 118 + 4 = 122 мм

колеса

d_ω2 = d₂ = 405,9 мм

d_a2 = d₂ + 2m_n = 405,9 + 2 * 4 = 413,9 мм

d_f2 = d₂ – 2,5m_n = 405,9 – 2,5 * 4 = 395,9 мм

b_ω2 = b_ω = 118 мм

2.8 Проверим зубчатую передачу на выносливость от действия контактных напряжений. Уточним величину коэффициента динамической нагрузки [1]. Для этого рассчитаем окружную скорость в зацеплении

υ = 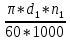= = 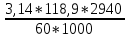18,3 м/с

Окружное усилие в зацеплении

F_t = 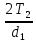= = 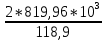13792,4 H

Удельная расчетная окружная сила

ω_Ht = 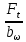K_HβK_HVK_Hα = 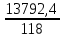* 1,04 * 1,2 * 1,06 = 154,6 H/мм

Определим [2] величину действующих нормальных контактных напряжений

---

Ϭ_H = z_Hz_Mz_ε 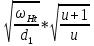= 1,72 * 271 * 077  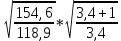= 456,6 < [Ϭ_H] = 466,5 МПа

Где

Z_H = 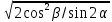= = 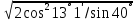1,72

Z_M = 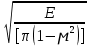= = 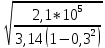271 H/мм

z_ε = 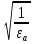= = 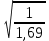0,77

Коэффициент торцевого перекрытия определим по формуле

ε_a = [ 1,88 – 3,2( 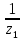+ 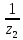)] cosβ = [1,88 – 3,2 ( 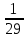+ 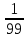)] 0,97437 = 1,69

Так как действующие напряжения не превышают допустимые, то условие прочности по контактной усталости можно считать выполненным.

2.9 Произведем проверочный расчет зацепления по напряжениям изгиба [2] Используя формулу

Ϭ_F = Y_FY_εY_β

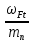
Эквивалентное число зубьев

шестерни

z_v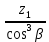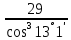1 = = = 31

колеса

z_v2 = 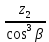= = 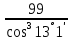107

По графику Y_F1 = 3,81; Y_F2 = 3,6

Определим слабое звено, по которому следует проверить прочность зуба. Рассчитаем отношение [ϭ_Н]/ Y_F:

для шестерни 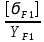= = 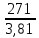71,5 МПа

для колеса 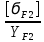= = 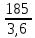51,5 МПа

Меньшая величина отношения у колеса, поэтому проверку производим для зуба колеса.

Коэффициент, учитывающий перекрытие зубьев Y_ε = 1 [2].

Коэффициент, учитывающий наклон зубьев Y

---

_β = 1- 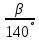= 0,91.

Удельная расчетная окружная сила

ω_Ft = K_FβK_FυK_Hα = * 1,22 * 1,1 * 1,06 = 166,27 H/мм

ϭ_F2 = Y_F2Y_εY_β = 3,6 * 1 * 0,91 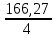= 136,18 МПа < [ϭ_F2] = 185 МПа

2.10 Проверим прочность зубьев при перегрузках:

по контактным напряжениям

ϭ_Hmax = ϭ_H 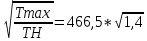= 542 МПа < [ϭ_Н] 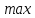= 756 МПа

Статическая прочность зуба колеса по контактным напряжениям при перегрузках обеспечена
по напряжениям изгиба

Ϭ_Fmax = ϭ_F2 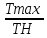= 131,8 * 1,4 = 184,52 МПа < [ϭ_F] 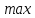= 216 МПа.

---

Смотрите также файлы

• Протокол 2009 г. М. п.doc

• Отчет по учебной практике по профессиональному модулю пм. 01 Предоставление турагентских услуг пм. 02 Предоставление услуг по сопровождению туристов.docx

• Протокол г. М. п. М. п. Инструкци я для учащихся по мерам безопасности.doc

• Карманная игротека вожатого.docx

• Протокол 2009 г. М. п.doc