Файл: Лабораторная работа 1 Изучение характеристик электростатического поля По дисциплине физика Выполнил Антипин Д. С.doc

Построенные силовые линии двух зарядов противоположного знака идут от одного заряда к другому и как бы стягивают их. Если в какой-либо точке пространства нет электрических зарядов, то через эту точку проходит только одна силовая линия. Таким образом, силовые линии непрерывны и не пересекаются. Произведены оценки величины напряженности поля в трех точках. Полученные результаты говорят о том, что в областях, где силовые линии расположены гуще, величина напряженности поля увеличивается, что соответствует формуле: .


Задание № 2. Исследование электростатического поля между двумя заряженными электродами различной геометрической формы.
Таблица 2. Результаты исследований электрического поля в ванне с плоским и круглым электродами различной полярности

Горизонтальная координата x, см	0,5	1,2	3,2	8	13,9	16,4	17,3	17,7	0,5	1,2	3,2	8	14,3
Вертикальная координата y, см	8	8	8	8	8	8	8	8	10	10	10	10	10
Потенциал φ, В	1	2	3	4	5	6	7	8	1	2	3	4	5
Горизонтальная координата x, см	1,2	3,2	8,1	15,3	0,5	1,2	3,2	8,3	17,6	0,5	1,2	3,2	8,5
Вертикальная координата y, см	12	12	12	12	14	14	14	14	14	16	16	16	16
Потенциал φ, В	2	3	4	5	1	2	3	4	5	1	2	3	4

---

Горизонтальная координата x, см	0,5	1,2	3,2	8	14,3	17,1	0,5	1,2	3,2	8,1	15,3	0,5	1,2	3,2	8,3
Вертикальная координата y, см	6	6	6	6	6	6	4	4	4	4	4	2	2	2	2
Потенциал φ, В	1	2	3	4	5	6	1	2	3	4	5	1	2	3	4

Горизонтальная координата x, см	17,7	0,5	1,2	3,3	8,5
Вертикальная координата y, см	2	0	0	0	0
Потенциал φ, В	5	1	2	3	4

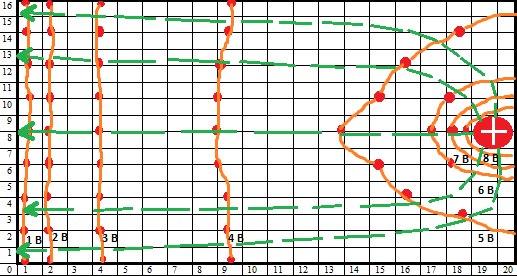
Рис. 3 Отрицательно заряженная плоскость и положительный электрод.
В точках с координатами (x=7;y=12), (x=10;y=12) и (x=13;y=12) найдем величину напряженности электрического поля по формуле (22):

---

_,

где - разность потенциалов между соседними эквипотенциальными линиями, - кратчайшее расстояние между ними.

Для восьмого варианта:

1. 
   Находим точку с координатами x=7;y=12 слева от неё находится эквипотенциальная линия 3В справа 4В, расстояние между ними 5 см. 1 клетка 1см. тогда:
   

2. 
   Находим точку с координатами x=10;y=12 слева от неё находится эквипотенциальная линия 4В справа 5В, расстояние между ними 7 см. 1 клетка 1см. тогда:
   

3. 
   Находим точку с координатами x=13;y=12 слева от неё находится эквипотенциальная линия 4В справа 5В, расстояние между ними 7 см. 1 клетка 1см. тогда:
   

Вывод:

Исследовано электростатическое поле отрицательно заряженной плоскости и положительно заряженного тонкого кольца радиусом 1 см (рис.3). Графически изображены сечения эквипотенциальных поверхностей с шагом 1 В от 1 В до 9 В. Видно, что вблизи электродов эквипотенциальные линии принимают форму источника, так например на примере ванны (рис.3) видно, что чем ближе эквипотенциальные линии к положительно заряженному кольцу, тем больше они принимают форму окружности, а чем ближе к плоскости, тем больше принимают форму прямой линии, что позволяет сделать вывод о том, что металлические электроды являются эквипотенциальными поверхностями. Построены силовые линии электростатического поля, произведены оценки величины напряженности поля в трех точках. Полученные результаты говорят о том, что в областях, где силовые линии расположены гуще, величина напряженности поля больше, что соответствует теоретическим ожиданиям.
Контрольные вопросы:

1. 
   Электрическое поле, его основные физические свойства. Электростатическое поле.
   

Электромагнитное поле, создаваемое неподвижными зарядами, называется электростатическим.

В каждой точке пространства оно характеризуется двумя величинами: напряженностью и потенциалом.

---

Напряженность (силовая характеристика поля) – векторная величина, численно равная силе, действующей на единичный положительный точечный заряд, помещенный в данную точку поля:



Единица измерения напряжённости - В/м (вольт на метр).

Потенциал (энергетическая характеристика электрического поля) - скалярная величина, численно равная потенциальной энергии единичного точечного положительного заряда, помещенного в данную точку поля:



Потенциал измеряется в вольтах: [1В= 1Дж/Кл]. Потенциал определяется с точностью до произвольной постоянной (как и потенциальная энергия) и может принимать положительные и отрицательные значения.

2. 
   Основные параметры электрического поля: напряжённость и потенциал, связь между ними (с выводом).
   

Напряжённость электрическогополя – это физическая величина, равная силе, действующей на положительный единичный точечный заряд, помещенный в данную точку поля.


Единица напряжённости электрического поля в системе СИ - .

Электрическое поле характеризуется также потенциалом – энергетической величиной, равной потенциальной энергии положительного единичного точеного заряда, помещенного в данную точку поля:



где - потенциал, - потенциальная энергия взаимодействия электрического заряда с полем, - величина этого заряда. Размерность потенциала в системе единиц СИ: .

Напряжённость и потенциал связаны между собой градиентом потенциала. Градиент потенциала показывает изменение потенциала вдоль нормали к эквипотенциальной поверхности. Градиент потенциала направлен в сторону обратную направлению напряжённости поля.

---

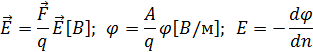
Напряжённость и потенциал - два физических параметра одного и того же объекта – электрического поля. Для нахождения связи между ними рассчитаем работу при бесконечно малом перемещении точечного заряда в электрическом по­ле из точки 0 в точку А (рисунок 1).

Элементарная механическая работа при таком перемещении вычисляется так:

(12)

В соответствие с формулой (11) эта же работа равна:

(13)



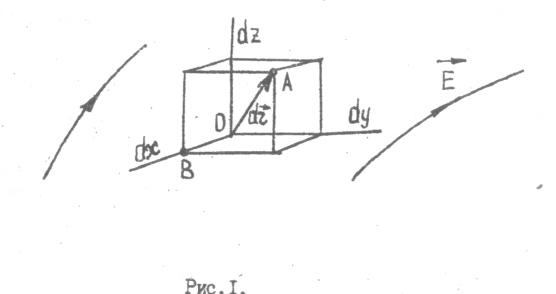
Рисунок 2. К расчёту связи напряжённости электрического поля с его потенциалом
Сопоставляя формулы (13) и (12) и учитывая явное выражение для силы (4), получим
(14)
Переместим теперь заряд из точки в точку на расстояние при фиксированных значениях координат и . В соответствии с формулой (13) получим:
(15)
где - проекция вектора напряжённости на ось . Последнюю фор­мулу перепишем так:
(16)
где частная производная находится путем дифференцирования по­тенциала по координате при фиксированных значениях и . По аналогии можно получить выражения для проекции вектора напряжённости на другие оси координат:

---