Добавлен: 02.02.2019
Просмотров: 5614
Скачиваний: 87
3)
(4) теңдеуден
![]() .
Бұдан х
а және у
в. Бұдан – а
х
а және –в
у
в. Сөйтіп, эллипстің нүктелері жазықтықтың
қабырғалары 2а және 2в болатын тік
төртбұрышпен шектелген бөлігінде
жатады.
.
Бұдан х
а және у
в. Бұдан – а
х
а және –в
у
в. Сөйтіп, эллипстің нүктелері жазықтықтың
қабырғалары 2а және 2в болатын тік
төртбұрышпен шектелген бөлігінде
жатады.
Теорема. Эллипстің кез келген М(х, у) нүктесі үшін төмендегі қатынас орындалады:
r 1
= a
–
1
= a
–![]() x,
r2
= a
+
x,
r2
= a
+
![]() x.
x.
Дәлелдеу. Жоғарыда r1 + r2 = 2a болатыны көрестілген. Сонымен қатар,геометьриялық кескіндеме бойынша:
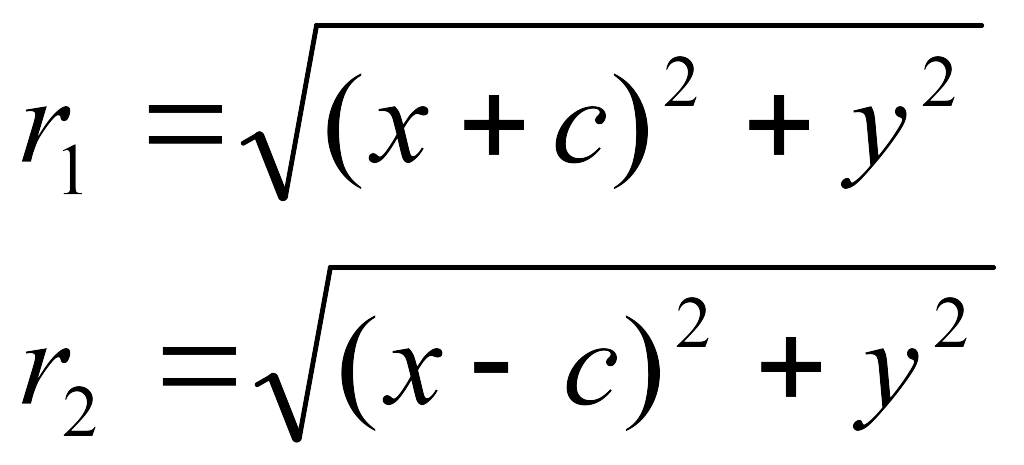 .
Осы формулалардағы у2
–ты эллипстің канондық теңдеуінен
тауып алып, алдыңғы формулаларға қойып
түрлендірсек, төмендегі теңдік шығады:
.
Осы формулалардағы у2
–ты эллипстің канондық теңдеуінен
тауып алып, алдыңғы формулаларға қойып
түрлендірсек, төмендегі теңдік шығады:
![]()
![]()
Дәл
осылайша
r2
= a
+
![]() x.
x.
А нықтама.
x = a/
нықтама.
x = a/![]() ;
x= -a/
;
x= -a/![]() .
теңдеулерімен анықталатын екі түзу
эллипстің директрисалары
деп
аталады.
.
теңдеулерімен анықталатын екі түзу
эллипстің директрисалары
деп
аталады.
Теорема.
Нүкте
эллипсте жату үшін оның фокусқа дейінгі
қашықтығының сәйкес директрисаға
дейінгі қашықтығына қатынасы
![]() эксцентриситетке тең болуы қажетті
және жеткілікті.
эксцентриситетке тең болуы қажетті
және жеткілікті.
Мысал.
![]() теңдеуімен берілген эллипстің сол жақ
фокусы мен төменгі төбесі арқылы өтетін
түзудің теңдеуін құр.
теңдеуімен берілген эллипстің сол жақ
фокусы мен төменгі төбесі арқылы өтетін
түзудің теңдеуін құр.
-
Эллипстің төменгі төбесінің координаталары: x = 0; y2 = 16; y = -4.
-
Сол жақ фокусының координаталары: c2 = a2 – b2 = 25 – 16 = 9; c = 3; F2(-3; 0).
-
Екі нүкте арқылы өтетін түзудің теңдеуі:
![]()
Мысал. F1(0; 0), F2(1; 1) фокустары мен үлкен осі 2 –ге тең болатын эллипстің теңдеуін жаз.
Эллипстің
теңдеуі мынадай:
![]() .
Мұнда а мен b жарты өстерін табу керек.
Фокустарының ара қашықтығы:
.
Мұнда а мен b жарты өстерін табу керек.
Фокустарының ара қашықтығы:
2c
=
![]() ,
сондықтан a2
– b2
= c2
= ½
,
сондықтан a2
– b2
= c2
= ½
Есеп
шарты бойынша 2а = 2, сонда а = 1, b =
![]()
Сонымен
эллипстің теңдеуі:
![]() .
.
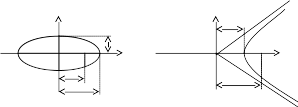
Гипербола және оның қасиеттері
Анықтама. Гипербола деп фокустары деп аталатын нүктелерден қашықтықтары айырмасының модулі сол фокустары арақашықтығынан (F1F2 = 2c) кем болатын тұрақты 2а санына тең болатын жазықтықтағы нүктелердің геометриялық орнын айтады, оны былайша белгілейді:
F1М - F2М = 2а (5) .
F1, F2 – гиперболаның фокустары. F1 = (-c; 0); F2(c; 0), F1F2 = 2c.
с – фокустары ара қашықтығының жартысы; 2а - тұрақты шама. F1М және F2М қашықтықтарын r1= F1М, r2= F2М деп белгілесек, онда (5) теңдік мына түрде жазылады:
r1 – r2= 2a (51)
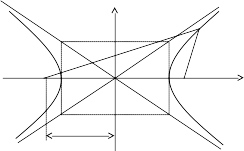
Гиперболаның бойынан кез келген М(х, у) нүкте алайық..
 y
y
M(x, y)
b
r1
r2
x
a
F1 А2(-а;0) А1(а;0) F2
c
Сонда:
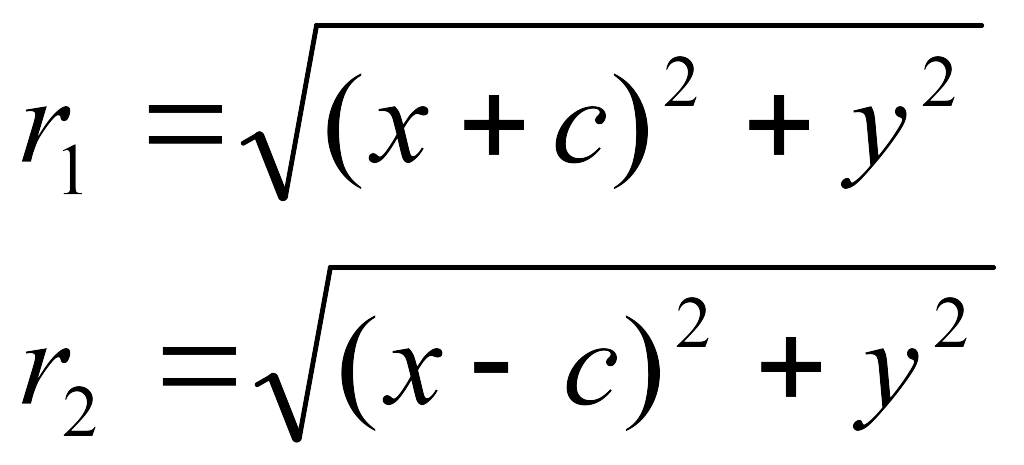
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
с2 – а2 = b2 деген белгілеме енгіземіз (геометриялық түрдегі бұл шама – кіші жарты ось)
![]()
![]()

Гиперболаның жабайы (канондық) теңдеуін алдық..
Гипербола фокустарын қосатын кесіндінің ортасына (О нүктеге), және координат осьтеріне қарағанда симметриялы.
2а гиперболаның нақты өсі деп аталады.
2b гиперболаның жорамал өсі деп аталады.
Гиперболаның қасиеттерін студенттерге өз беттерімен қарастыруға тапсырылады.
Г иперболаның
екі асимптотасы болады және олар
иперболаның
екі асимптотасы болады және олар
![]() теңдеулері арқылы беріледі.
теңдеулері арқылы беріледі.
Анықтама.
![]() қатынасы гиперболаның
эксцентриситеті деп
аталады, мұндағы с – фокустары қашықтығының
жартысы, а –нақты жарты өсь.
қатынасы гиперболаның
эксцентриситеті деп
аталады, мұндағы с – фокустары қашықтығының
жартысы, а –нақты жарты өсь.
с2 – а2 = b2 екеніні ескерсек:
![]()
![]()
Егер
а
= b,
![]() =
=
![]() болса, онда
гипербола
теңбүйірлі
(тең
қабырғалы)
деп аталады.
болса, онда
гипербола
теңбүйірлі
(тең
қабырғалы)
деп аталады.
 Анықтама.
Гиперболаның нақты өсіне перпендикуляр,
оның центріне қарағанда симметриялы
және одан a/
Анықтама.
Гиперболаның нақты өсіне перпендикуляр,
оның центріне қарағанда симметриялы
және одан a/![]() қашықтықта болатын екі түзу гиперболаның
директрисалары
деп
аталады.Олардың теңдеулері:
қашықтықта болатын екі түзу гиперболаның
директрисалары
деп
аталады.Олардың теңдеулері:
![]() .
.
Теорема. Егер r – гиперболаның кез келген М нүктесінен қандай да бір фокусына дейінгі қашықтығы, ал d – осы фокусқа сәйкес директрисаға дейінгі қашықтығы болса,онда r/d қатынас – эксцентриситетке тең тұрақты шама.
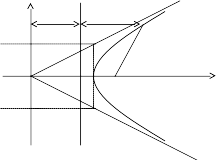
Дәлелдеуі. Гиперболаны схемалық түрде кескіндейік:
 y
y
a/e d
M(x, y)
r1
0 a F1 x
OF1 = c. Геометриялық кескінедемеден мыналарды жазуға болады:
a/![]() e
+ d
= x,
сондықтан
d
= x
– a/
e
+ d
= x,
сондықтан
d
= x
– a/![]() e.
(x – c)2
+ y2
= r2
e.
(x – c)2
+ y2
= r2
Гиперболаның
канондық теңдеуінен:
![]() ,
с учетом b2
= c2
– a2:
,
с учетом b2
= c2
– a2:
![]()
![]()
![]()
Сонда
с/a
=
![]() болғандықтан,
r
=
болғандықтан,
r
=
![]() x
– a.
x
– a.
Сонымен:
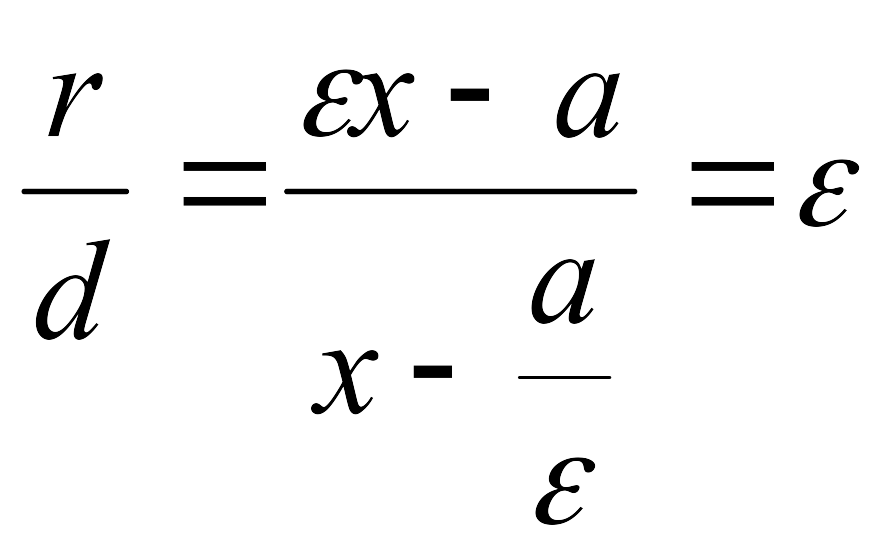 .
.
Гиперболаның сол жақтағы тармағы үшін дәлелдеме осы тәріздес.
Пример.
Төбелері
мен фокустары
![]() эллипсінің сәйкес төбелері мен
фокустарында болатын гиперболаның
теңдеуін жаз.
эллипсінің сәйкес төбелері мен
фокустарында болатын гиперболаның
теңдеуін жаз.
Эллипс үшін : c2 = a2 – b2.
Гипербола үшін: c2 = a2 + b2.
![]()
![]()
![]()
![]()
![]()
Гиперболаның
теңдеуі:
![]() .
.
Мысал.
Егер гиперболаның эксцентриситеті
2-ге тең, ал фокустары
![]() теңдеуімен берілген эллипстің фокустарымен
беттессе, онда гиперболаның теңдеуін
жаз.
теңдеуімен берілген эллипстің фокустарымен
беттессе, онда гиперболаның теңдеуін
жаз.
Шешу. Эллипстің фокустық ара қашықтығын табамыз: c2 = 25 – 9 = 16.
Гипербола
үшін:
c2
= a2
+ b2
= 16,
![]() =
c/a
= 2; c
= 2a;
c2
= 4a2;
a2
= 4;
=
c/a
= 2; c
= 2a;
c2
= 4a2;
a2
= 4;
b2 = 16 – 4 = 12.
Сонда
![]() - гиперболаның
теңдеуі болады.
- гиперболаның
теңдеуі болады.
Парабола және оның қасиеттері
Анықтама. Парабола деп фокусы деп аталатын нүктеден ара қашықтығы центрі арқылы өтпейтін директрисасы деп аталатын берілген түзуден бірдей ара қашықтықта болатын жазықтықтағы нүктелердің жиынын айтады.
Координат басын фокус пен директрисаның ортасына орналастырамыз.
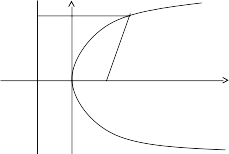 у
у
 А М(х, у)
А М(х, у)

О F x


p/2 p/2
р шама (фокустан директрисаға дейінгі қашықтық) параболаның параметрі деп аталады. Параболаның жабайы теңдеуін қорытып шығарайық.
Геометриялық кескіндемеден: AM = MF; AM = x + p/2;
MF2 = y2 + (x – p/2)2
(x + p/2)2 = y2 + (x – p/2)2
x2 +xp + p2/4 = y2 + x2 – xp + p2/4

y2 = 2px (*)
x = -p/2 - директрисаның теңдеуі.
Параболаның қасиеттері:
-
(*) теңдеудегі у жұп дәрежелі болғандықтан, парабола Ох өсіне қарағанда симметриялы, Ох өсі параболаның симметрия өсі болады.
-
р0 болғандықтан, (*) теңдеуден х0. Сондықтан, парабола Оу өсінің оң жағында орналасады.
-
х 0 болғанда, у 0. Демек, парабола координат басы арқылы өтеді.
-
х шектеусіз өскен сайын у-тің модулі де шектеусіз өседі. О(0; 0) нүкте параболаның төбесі , ҒМ г М нүктесінің фокальдық радиусыболады.
y2 = - 2px , х2 = 2pу, х2 = - 2pу (р0 ) теңдеулері де параболаларды анықтайды.
Мысал. у2 = 8х параболаның бойынан директрисаға дейінгі қашықтығы 4 – ке тең болатын нүктені тап.
Шешу. Параболаның теңдеуінен р = 4 табамыз.
r = x + p/2 = 4; Сонда x = 2; y2 = 16; y = 4. Ізделінді нүктелер: M1(2; 4), M2(2; -4).
КЕҢІСТІКТЕГІ АНАЛИТИКАЛЫҚ ГЕОМЕТРИЯ
4. Кеңістіктегі жазықтық.
-
Берілген М0(x0, y0, z0) нүкте арқылы өтіп,
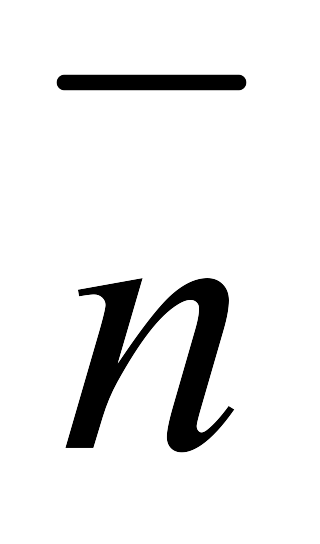 =(A,B,C)
нормаль векторына перепендикуляр
жазықтықтың теңдеуі
=(A,B,C)
нормаль векторына перепендикуляр
жазықтықтың теңдеуі
A(x-x0)+B(y-y0)+C(z-z0)=0
2.
Ax+By+Cz+D=0 теңдеуі, мұндағы А, В, С
коэффициенттерінің кемінде біреу нөлге
тең емес, жазықтықтың жалпы теңдеуі деп
аталады.
Мұндағы
![]() =(A,B,C)
нормаль векторы.
=(A,B,C)
нормаль векторы.
3.
Жазықтықтың
нормаль теңдеуі.
Ax+By+Cz+D=0 теңдеуін нормаланған теңдеуіне
келтіру үшін, оны
![]() нормалаушы көбейткішіне көбейту қажет.
Егер D
нормалаушы көбейткішіне көбейту қажет.
Егер D![]() 0
, болса, онда бұл көбейткіштің таңбасы
D-
нің таңбасына қарама – қарсы алынады.
Ал егерде D=0
болса, онда
0
, болса, онда бұл көбейткіштің таңбасы
D-
нің таңбасына қарама – қарсы алынады.
Ал егерде D=0
болса, онда
![]() -
ның таңбасы ретінде екі таңбаның кез
келгенің алуға болады, яғни Ax+By+Cz=0
теңдеудің сол жағын
-
ның таңбасы ретінде екі таңбаның кез
келгенің алуға болады, яғни Ax+By+Cz=0
теңдеудің сол жағын
![]() векторының ұзындығына бөлеміз.
векторының ұзындығына бөлеміз.
М1(x1 ,y1 ,z1), М2(x2 ,y2 ,z2), М3(x3 ,y3 ,z3) үш нүктеден өтетің жазықтықтың теңдеуі анықтауыш арқылы табылады
![]()
Кеістіктегі аналитикалық геометрия
Жазықтықтағы тәрізді кеңістікте де кез келген сызық координаталары қандай да бір таңдалып алынған координат системасында F(x, y, z) = 0 (1) теңдеуін қанағаттандыратын нүктелер жиыны ретінде анықталады.
(1) теңдеу кеңістіктегі сызықтың теңдеуі болады.
Сонымен қатар кеңістікте сызық басқаша да анықталуы мүмкін. Оны әрқасысы қандай да бір теңдеумен берілген екі беттің қиылысу сызығы деп қарауға болады.
Айталық F(x, y, z) = 0 и Ф(x, y, z) = 0 – L сызығы бойынша қиылысатын беттердің теңдеулері болсын.
Сонда
![]() теңдеулер жүйесін кеңістіктегі
сызықтың теңдеуі
деп атайды.
теңдеулер жүйесін кеңістіктегі
сызықтың теңдеуі
деп атайды.
Кеңістікте нүкте мен бағыттаушы векторы арқылы берілген түзудің теңдеуі
Кез
келген түзу мен оған параллель
![]() (m,
n, p) векторын алайық..
(m,
n, p) векторын алайық..
![]() векторы
түзудің бағыттаушы
векторы деп
аталады.
векторы
түзудің бағыттаушы
векторы деп
аталады.
Түзу бойынан кез келген М0(x0, y0, z0) және M(x, y, z) нүктелерін аламыз..
 z
z
![]() M1
M1
M0
![]()
![]()
0 y
x
Бұл
нүктелердің
радиус- векторларын
![]() и
и
![]() арқылы
белгілейік,
сонда
арқылы
белгілейік,
сонда
![]() -
-
![]() =
=
![]() .
.

![]() и
и
![]() векторлары
коллинеар
болғандықтан,
векторлары
коллинеар
болғандықтан,
![]() =
=
![]() t
қатынасы орындалады,
мұндағы
t
– кез
келген параметр.
t
қатынасы орындалады,
мұндағы
t
– кез
келген параметр.
![]() =
=
![]() t
теңдіктен мынау шығады:
t
теңдіктен мынау шығады:
![]() -
-
![]() =
=
![]() t
. Бұдан
t
. Бұдан
![]() =
=
![]() +
+
![]() t
(2) .
t
(2) .
Бұл теңдеуді түзудің кез келген нүктесінің координаталары қанағаттандыратындықтан, (2) теңдеу түзудің параметрлік теңдеуі болады.
Бұл векторлық теңдеу координаталық формада былайша жазылады:
![]()
Бұл жүйені түрлендіріп t параметрге теңестіру арқылы кеңістіктегі түзудің канондық (жабайы) теңдеуін аламыз:
![]() .
.
Түзудің
параметрлік теңдеуі канондық теңдеуден
шығады. Айталық бізге түзудің канондық
теңдеуі берілсін.
![]() (1). Осыны t
параметрге теңестіреміз. Сонда:
(1). Осыны t
параметрге теңестіреміз. Сонда:
![]() =t
,
бұдан
=t
,
бұдан
![]() ,
немесе
,
немесе
![]()
Анықтама.
Түзудің
бағыттаушы
косинустары
деп
![]() векторының
бағыттаушы косинустарын айтады және
олар төмендегі формулалар бойынша
анықталады:
векторының
бағыттаушы косинустарын айтады және
олар төмендегі формулалар бойынша
анықталады:
![]() ;
;
![]()
![]() .
.
Бұдан мынаны аламыз: m : n : p = cos : cos : cos.
m,
n,
p
сандары
түзудің бұрыштық
коэффициенттері
деп аталады.
![]() -
нөлдік
емес вектор
болғандықтан,
m,
n
и p
бір
уақытта нөлге тең бола алмайды, алайда
бұл сандардың біреу не екуі нөлге тең
болуы мүмкін. Бұл жағдайда түзудің
теңдеуінен сәйкес алымдарын нөлге
теңестіруге тура келеді.
-
нөлдік
емес вектор
болғандықтан,
m,
n
и p
бір
уақытта нөлге тең бола алмайды, алайда
бұл сандардың біреу не екуі нөлге тең
болуы мүмкін. Бұл жағдайда түзудің
теңдеуінен сәйкес алымдарын нөлге
теңестіруге тура келеді.
Кеңістікте екі нүкте арқылы өтетін тұзудің теңдеуі
Егер кеңістіктегі түзудің бойынан M1(x1, y1, z1) және M2(x2, y2, z2) екі нүкте берілсе, онда олар түзудң жоғарыдағы теңдеуін қанағаттандыруы кере, яғни:
![]() .
.
Сонымен қатар М1 нүкте үшін мынаны жазамыз:
![]() .
.
Осы теңдеулерді біріктіп шешу арқылы мынаны аламыз:
![]()
 .
.
Бұл екі нүкте арқылы берілген түзудің теңдеуі.
Кеңістіктегі түзудің жалпы теңдеуі
Түзуді
екі жазықтықтыңтың қиылысу арқылы былай
анықталады:
![]() . Бұлардың нормаль ваекторларының
координаталары былайша анықталады:
. Бұлардың нормаль ваекторларының
координаталары былайша анықталады:
![]() (A1,
B1,
C1),
(A1,
B1,
C1),
![]() (A2,
B2,
C2);
(A2,
B2,
C2);
Түзудің
бағыттауыш векторы
![]()
![]() ,
,![]() векторларына
перпендикуляр. Сонда
векторларына
перпендикуляр. Сонда
![]() =
=![]() x
x![]()
![]()
![]() .
.
Жазықтық векторлық формада төмендегі теңдеу арқылы берілуі мүмкін:
![]()
![]() +
D
= 0, где
+
D
= 0, где
![]() -
жазықтықтың
нормалі;
-
жазықтықтың
нормалі;
![]() -Жазықтықтың
кез келген нүктесінің радиус - векторы.
-Жазықтықтың
кез келген нүктесінің радиус - векторы.
Айталық
кеңістікте екі жазықтық берілсін:
![]()
![]() +
D1
= 0 и
+
D1
= 0 и
![]()
![]() +
D2
= 0,нормаль
векторлардың координаталары::
+
D2
= 0,нормаль
векторлардың координаталары::
![]() (A1,
B1,
C1),
(A1,
B1,
C1),
![]() (A2,
B2,
C2);
(A2,
B2,
C2);
![]() (x,
y,
z).
(x,
y,
z).
Түзудің жалпы теңдеуі параметрлік түрде беріледі:
![]()

Түзудің координаталық формадағы жалпы теңдеуі:
![]()

Бұл практика жүзінде есеп теңдеуі жалпы түрде берілген түзулердің теңдеулерін канондық түрге келтіру болып табылады.
Ол үшін түзудің кез келген нүктесін және m, n, p сандарын табады.
Бұл ұшін түзудің бағыттаушы векторы берілген жазықтықтардың нормаль векторлардың векторлық көбейтіндісі арқылы анықталады.
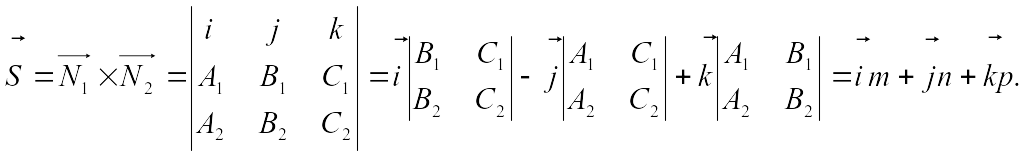
Мысалы.
Түзудің
![]() канондық теңдеуін тап.
канондық теңдеуін тап.
Түзудің кез келген нүктесін табу үшін х = 0 деп аламыз, содан кейін осы мәнді берілген теңдеулер жүйесіне қоямыз.
![]() ,
т.е. А(0, 2, 1).
,
т.е. А(0, 2, 1).
Түзудің бағыттаушы векторының компоненттерін табамыз:
![]()
Сонда түзудің канондық теңдеуі:
![]()
Мысал.
Түзудің
![]() теңдеуін канондық (жабайы) түрге кеклтір.
теңдеуін канондық (жабайы) түрге кеклтір.
Жоғарыдағы екі жазықтықтың қиылысуы арқылы берілген тұзудің кез келген нүктесін табу үшін z = 0 деп аламыз.Сонда:
![]() ;
;
2x – 9x – 7 = 0;
x = -1; y = 3;
Сонымен: A(-1; 3; 0).
Түзудің
бағыттаушы векторы:
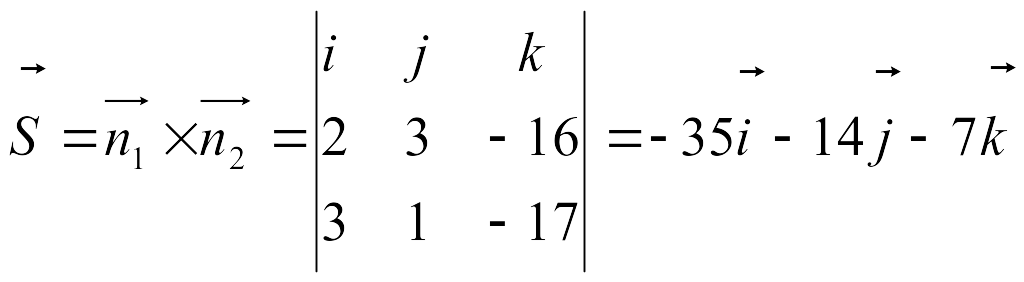 .
.
Сонымен:
![]()
![]()
1
0
![]()
Кеңістіктегі екі жазықтық арасындағы бұрыш осы жазықтықтардың нормаль векторларының арасындағы 1 бұрышпен мынадай қатынаста болады: = 1 или = 1800 - 1, яғни cos = cos1.
1 бұрышын анықтайық. Жазықтықтар төмендегі теңдеулер арқылы берілсін:
![]() ,
мұндағы
,
мұндағы
![]() (A1,
B1,
C1),
(A1,
B1,
C1),
![]() (A2,
B2,
C2).
Нормаль
векторлардың арасындағы бұрышты скаляр
көбейтіндіден табамыз:
(A2,
B2,
C2).
Нормаль
векторлардың арасындағы бұрышты скаляр
көбейтіндіден табамыз:
![]() .
.
Сонымен жазықтықтар арасындағы бұрыш төмендегі формула бойынша анықталады:

![]()
Косинустың таңбасын таңдау жазықтықтар арасындағы қандай бұрышты (сүйір немесе онымен іргелес доғал бұрышты) табатынымызға байланысты.
Жазықтықтардың параллельдік және перпендикулярлық шарттары
Жоғарыдағы шыққан формуланың негізінде жазықтықтардың арасындағы бұрышты табу үшін жазықтықтардың параллельдік және перпендикулярлық шарттарын табуға болады.
 Жазықтықтар
перпендикуляр болу үшін сол жазықтықтардың
арасындағы бұрыштың косинусы нөлге
тенң болуы қажетті және жеткілікті.
Бұл
шарт орындалу үшін
төмендегі шарт орындалу керек.
Жазықтықтар
перпендикуляр болу үшін сол жазықтықтардың
арасындағы бұрыштың косинусы нөлге
тенң болуы қажетті және жеткілікті.
Бұл
шарт орындалу үшін
төмендегі шарт орындалу керек.
![]()
 Жазықтықтар
параллель болу үшін олардың нормаль
векторлары коллинеар болуы керек, яғни
Жазықтықтар
параллель болу үшін олардың нормаль
векторлары коллинеар болуы керек, яғни
![]()
![]() .
Бұл шарт орындалу үшін төмендегі теңдік
орындалу кернек: .
.
Бұл шарт орындалу үшін төмендегі теңдік
орындалу кернек: .
![]()
Кеңістіктегі түзулер арасындағыбұрыш
Айталық кеңістікте екі түзу өздерінің параметрлік теңдеулерімен берілсін:
l1:
![]()
l2:
![]()
![]()
Түзулер арасындағы бұрыш және олардың бағыттаушы векторлары арасындағы 1 бұрыш = 1 немесе = 1800 - 1 қатысымен байланысты. Бағыттаушы векторлардың арасындағы бұрыш векторлардың скаляр көбейтіндісінен шығады, яғни:

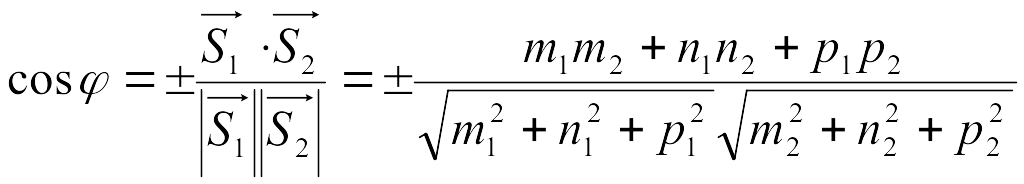 .
.
d1
және d2
түзулер
![]() ,
,
![]() түрінде берілсе онда екі түзудің
арасындағы бұрыш мына формуламен
анықталады
түрінде берілсе онда екі түзудің
арасындағы бұрыш мына формуламен
анықталады![]() .
.
Кеңістікте түзулердің параллельдігі мен перпендикулярлық шарттары
Екі түзу параллель болу үшін олардың бағыттаушы векторлары коллинеар болуы қажетті және жеткілікті, яғни векторлардың сәйкес координаталары пропорционал.
![]()

 Екі
түзу перпендикуляр болу үшін олардың
бағыттаушы векторлары перпендикуляр
болуы қажетті және жеткілікті, яғни
олардың арасындағы бұрыштың косинусы
нөлге тең.
Екі
түзу перпендикуляр болу үшін олардың
бағыттаушы векторлары перпендикуляр
болуы қажетті және жеткілікті, яғни
олардың арасындағы бұрыштың косинусы
нөлге тең.
![]()
Түзу мен жазықтық арасындағы бұрыш
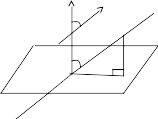
Анықтама. Түзу мен жазықтық арасындағы бұрыш деп түзу мен оның жазықтықтағы проекциясының арасындағы кез келген бұрышты айтады.
![]()
![]()
Айталық
жазықтық
![]() теңдеуімен,
ал түзу
-
теңдеуімен,
ал түзу
-
![]() теңдеуімен берілсін.
Геометриялық
кескіні бойынша
(суретті
қара.)
ізделінді
бұрыш
= 900
- ,
мұндағы
- угол
теңдеуімен берілсін.
Геометриялық
кескіні бойынша
(суретті
қара.)
ізделінді
бұрыш
= 900
- ,
мұндағы
- угол
![]() и
и
![]() векторлары
арасындағы бұрыш.
Бұл
бұрыш төмендегі формула бойынша
табылады:
векторлары
арасындағы бұрыш.
Бұл
бұрыш төмендегі формула бойынша
табылады:
![]()
![]()
![]()

Координаталық
формада:
![]()
Кеңістікте түзу мен жазықтықтың параллельдік және перпендикулярлық шарттары
Түзу мен жазықтық параллель болу үшін жазықтықтың нормаль векторы мен түзудің бағыттайшы векторлары перпендикуляр болуы қажетті және жеткілікті. Ол үшін сол векторлардың скаляр көбейтіндісі нөлге тең болуы қажетті.
![]()
Түзу мен жазықтық перпендикуляр жазықтықтың нормаль векторы түзудің бағыттаушы векторы коллинеар болуы қажетті және жеткілікті. Бұл шарт орындалады, егер осы векторлардың скаляр көбейтіндісі нөлге тең болса.

![]()
Айналу беттері
Анықтама. Қандай да бір қисықтың қозғалмайтын d түзуін айналудан шыққан бет d осін айналудан шыққан бет деп аталады.
Егер тік бұрышты координат системасында беттің теңдеуі F(x2 + y2, z) = 0 түрінде берілсе, онда бет Оz осін айналудан шыққан бет болады.
Дәл сол сияқты: F(x2 + z2, y) = 0 – Оу осін айналудан шыққан бет,
F(z2 + y2, x) = 0 – Ох осін айналудан шыққан бет.
Дербес жағдайдағы айналу беттерінің теңдеулерін жазайық.
-
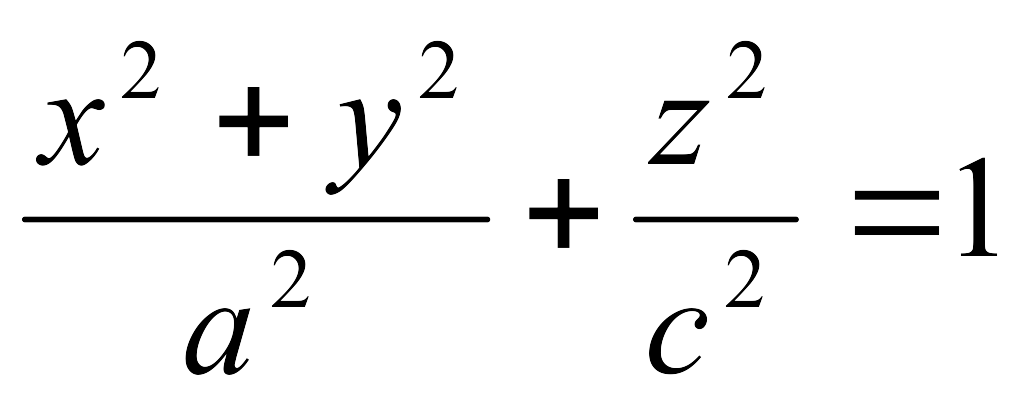 -
айналу
эллипсоиды
-
айналу
эллипсоиды
-
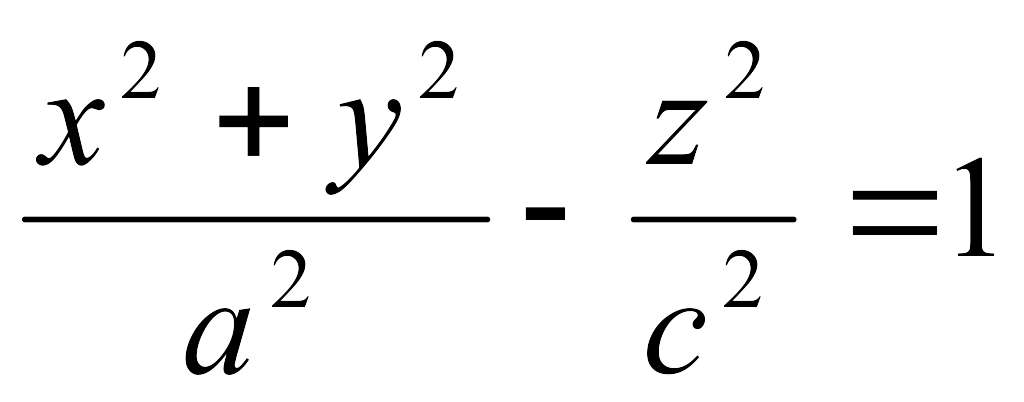 -
бір
қуысты айналу
гиперболоиды
-
бір
қуысты айналу
гиперболоиды -
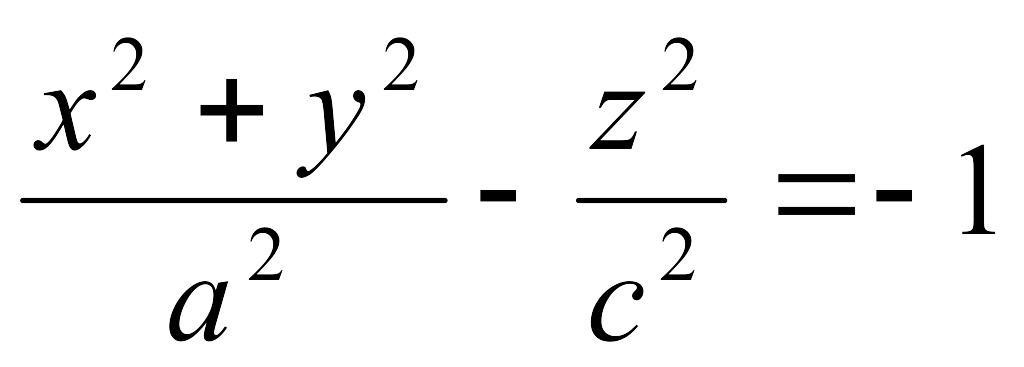 -
екі
қуысты айналу гиперболоиды
-
екі
қуысты айналу гиперболоиды
-
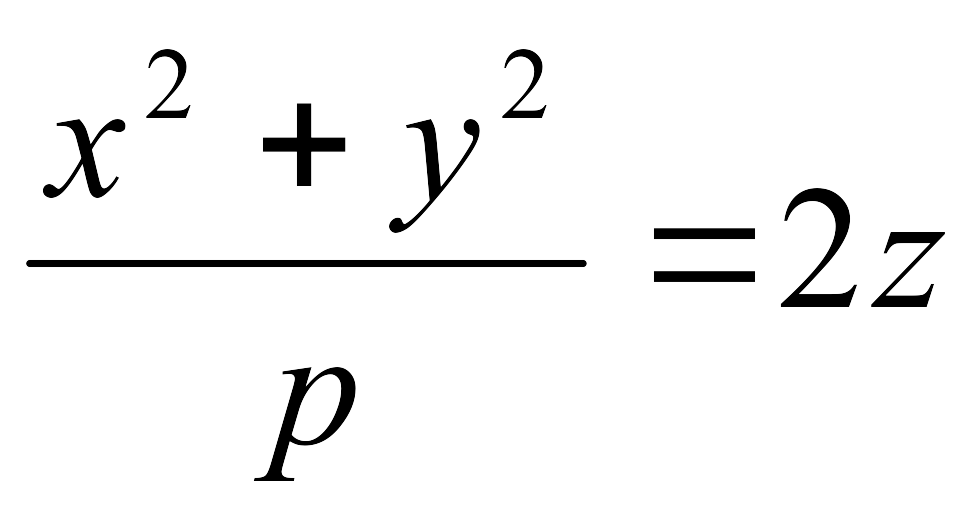 -
айналу
параболоид
-
айналу
параболоид
Дәл осылайша жоғарыдағы айналу беттердің теңдеулерін айналу осьтері Ох немесе Оу болған жағдайда да жазуға болады
А лайда
жоғарыдағы беттер жалпы жағдайдағы
екінші ретті беттердің дербес жағдайы
боп табылады. Олардың кейбіреулерін
төменде қарастырамыз.
лайда
жоғарыдағы беттер жалпы жағдайдағы
екінші ретті беттердің дербес жағдайы
боп табылады. Олардың кейбіреулерін
төменде қарастырамыз.